📍 <프로그래밍 대회에서 배우는 알고리즘 문제 해결 전략(a.k.a. 종만북)>으로 공부한 내용을 정리한 게시글입니다.
📍 ChatGPT에게 추천 받은 분할 정복 문제 3개

DP가 꽤나 어려워서 저번에 이어 또 DP 문제를 풀어보았다.

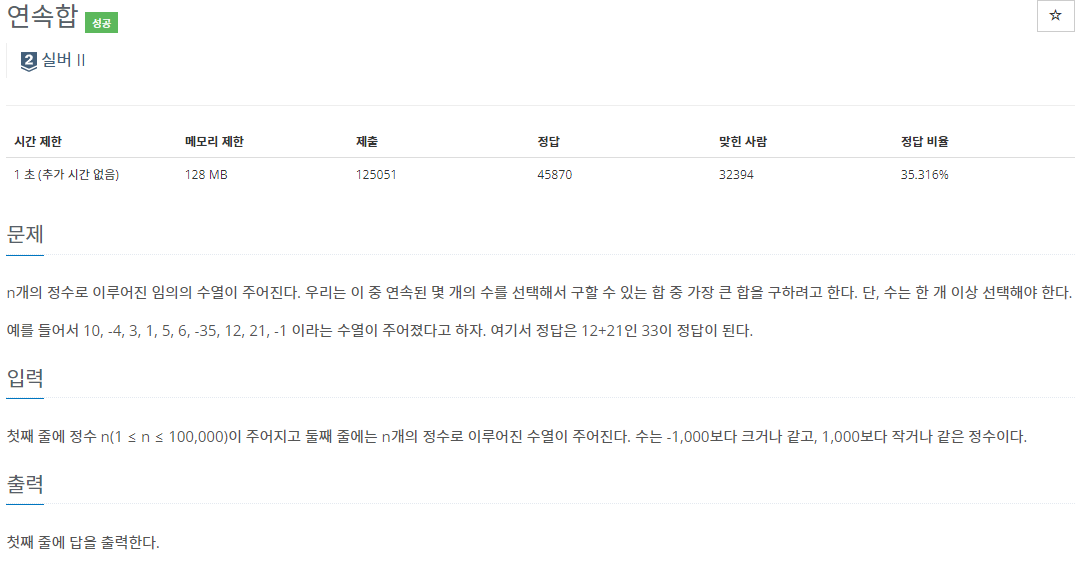
1912 연속합

#include <iostream>
#include <algorithm>
using namespace std;

int n;
int num[100002], cache[100002];
int s = 0;

int main() {
	ios::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);
	
	std::cin >> n;
	for (int i = 0; i < n; i++) {
		cin >> num[i];
	}

	int result = num[0];
	cache[0] = num[0];
	for (int i = 1; i < n; i++) {
		cache[i] = max({ num[i], cache[i - 1] - num[s] + num[i], cache[i - 1] + num[i] });
		if (cache[i] == num[i]) s = i;
		else if (cache[i] == cache[i - 1] - num[s] + num[i]) ++s;
		if (cache[i] >= result) result = cache[i];
	}

	cout << result;
}

얼마 전에 비슷한 문제를 풀어서 start 지점을 지정하고 풀어야한다는걸 알아서 금방 풀었다.

점화식

cache[i] = max({ num[i], cache[i - 1] - num[s] + num[i], cache[i - 1] + num[i] });

(현재 값, 직전 캐시 + 현재 값, 직전 캐시 + 현재 값 - 시작 값) 중 가장 큰 값을 저장해주면 된다. 고른 값에 따라 start 위치를 지정해주어야 한다.

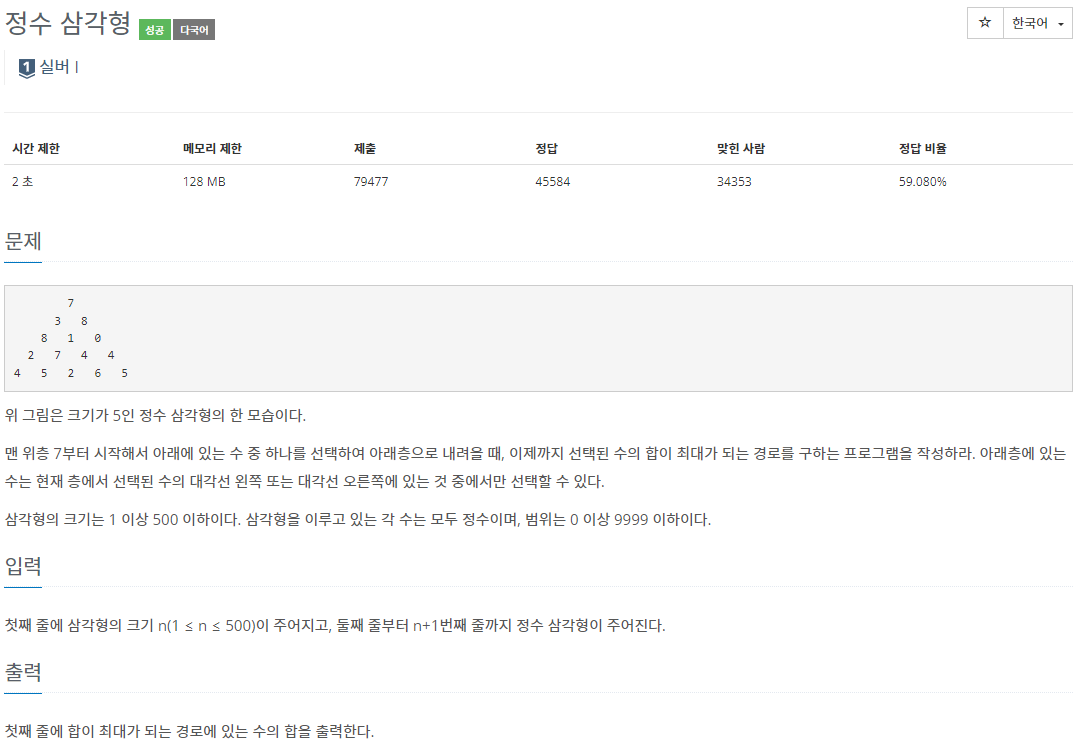
1932 정수 삼각형

#include <iostream>
#include <algorithm>
using namespace std;

int tree[501][501];
int cache[501][501];
int main() {
	ios::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);

	int n;
	cin >> n;
	for (int i = 0; i < n; i++) {
		for (int j = i; j >= 0; j--) {
			cin >> tree[i][j];
		}
	}

	cache[0][0] = tree[0][0];

	for (int i = 1; i < n; i++) {
		for (int j = 0; j <= i; j++) {
			if (j == 0) cache[i][j] = tree[i][j] + cache[i - 1][j];
			else if (j == i) cache[i][j] = tree[i][j] + cache[i - 1][j - 1];
			else
				cache[i][j] = tree[i][j] + max(cache[i - 1][j - 1], cache[i - 1][j]);
		}
	}
	cout << *max_element(cache[n - 1], cache[n - 1] + n);
}

더한 값을 전부 다 저장하고, 마지막 행 값 중 가장 큰 값을 출력하는게 나을 것 같다고 생각했다. 현재 값 + 접근할 수 있는 윗 행의 값 2개 중 큰 값을 차곡차곡 더했다.

❕max_element(배열의 시작 주소, 배열의 크기) : 주솟값 반환

DP 재귀

#include <iostream>
#include <cstring>
using namespace std;

int a;
int triangle[500][500];
int cache[500][500];

int sum(int x, int y) {
	if (x == a - 1) return triangle[x][y];
	int& ret = cache[x][y];
	if (ret != -1) return ret;
	return ret = triangle[x][y] + max(sum(x + 1, y), sum(x + 1, y + 1));
}

int main() {
	ios::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);
	memset(cache, -1, sizeof(cache));
	cin >> a;

	for (int i = 0; i < a; i++) {
		for (int j = 0; j <= i; j++) {
			cin >> triangle[i][j];
		}
	}
	cout << sum(0, 0);
	return 0;

}

재귀로 하면 for문과 다르게 전체 범위를 체크하지 않아도 된다.(위의 방식이 과연 DP였을까..? 걍 메모이제이션만 쓴 듯)
📍 return에서 cache update하는거 잊지 않기!!

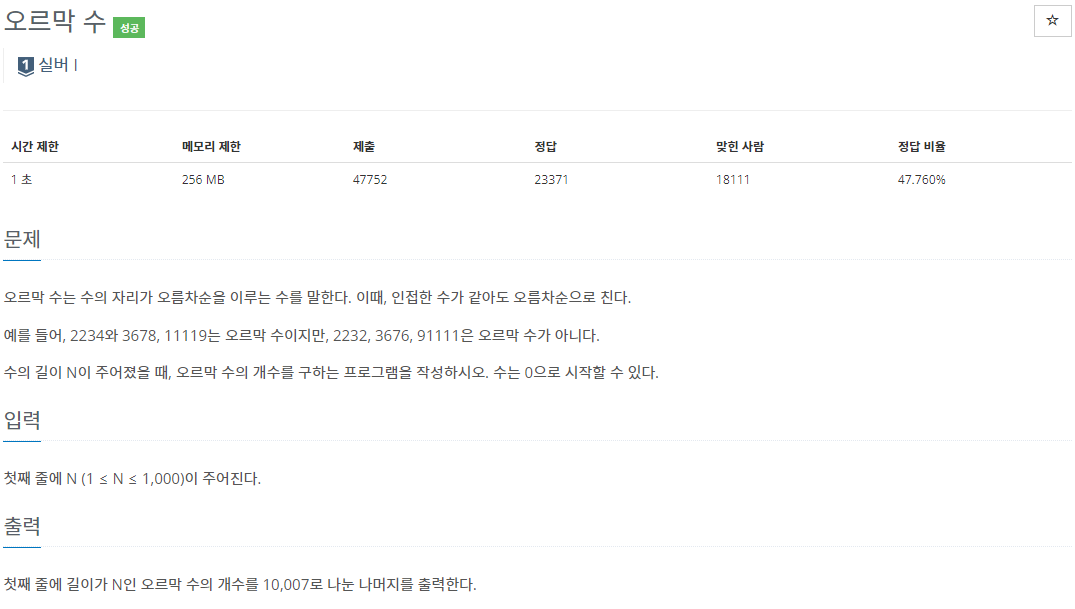
11057 오르막 수

#include <iostream>
using namespace std;

#define MOD 10007;
long long cache[1002][11];


int main() {
	ios::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);

	int n;
	cin >> n;

	for (int i = 0; i <= 10; i++) cache[1][i] = i + 1;
	for (int i = 0; i <= n; i++) cache[i][0] = 1;

	for (int i = 2; i <= n; i++) {
		for (int j = 1; j < 10; j++) {
			cache[i][j] = cache[i][j - 1] + cache[i - 1][j];
			cache[i][j] %= MOD;
		}
	}

	cout << cache[n][9] % MOD;
}

처음엔 점화식을 뺄셈으로 세워서 나머지로 인해 값이 음수가 되는 현상이 발생했다. 그래서 바로 덧셈 점화식으로 변경.
뺄셈 점화식은 맨 앞자리 수가 0인 수부터 9인 수로 올라가서 생각하기 쉬워서 이것부터 떠올렸던 것 같다.

n자리 오르막 수의 개수를 구하는 방법

0으로 시작하는 오르막 수의 개수 =  n-1자리 오르막 수의 개수
1으로 시작하는 오르막 수의 개수 = 0으로 시작하는 n자리 오르막 수의 개수 - 0으로 시작하는 n-1자리 오르막 수의 개수
... 이하 생략

뺄셈 점화식(실패)

cache[i][j] = cache[i-1][j] - cache[i-1][j-1];

(이 경우 특정 변수에 해당 열의 총합을 구해야한다)
그런데 위의 방식처럼 뺄셈으로 하는 경우 MOD로 인해 음수가 생긴다!! 그러므로 위 방식은 불가능하다. 덧셈으로 바꾼 점화식은 다음과 같다

덧셈 점화식(성공)

cache[i][j] = cache[i][j - 1] + cache[i - 1][j];

j 이하로 시작하는 i자리 오르막 수의 개수를 구할 수 있다. 이렇게 하면 [i][9]에는 해당 행의 총합이 들어가므로 따로 더해줄 필요도 없다!