Image Segmentation

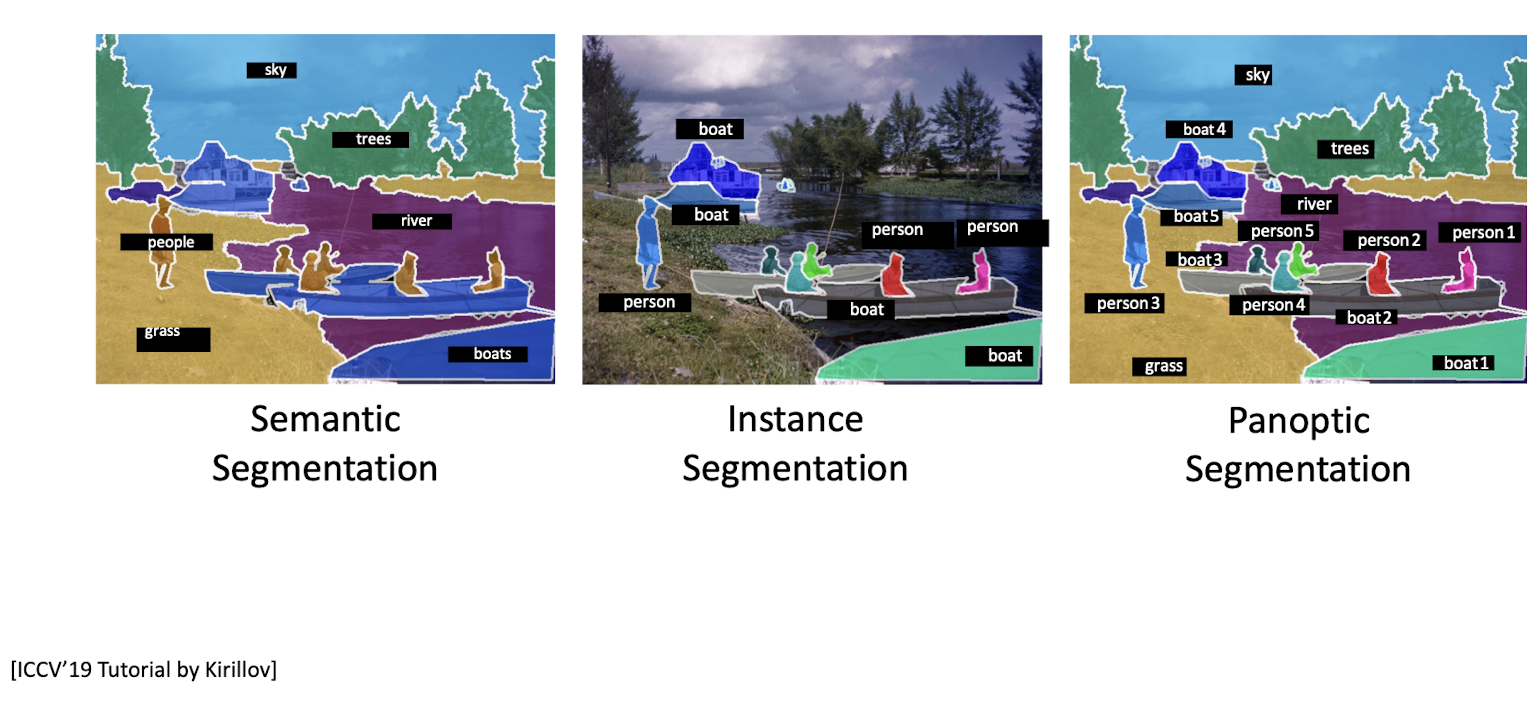
Semantic Segmentation : labeling per-pixel + No objects (개체를 찾지 않음)

Instance Segmentation : pixel labeling Things(O), Stuff (X)

Panoptic Segmentation : all pixel labeling Things(O), Stuff (O)

---

Semantic Segmentation

Task

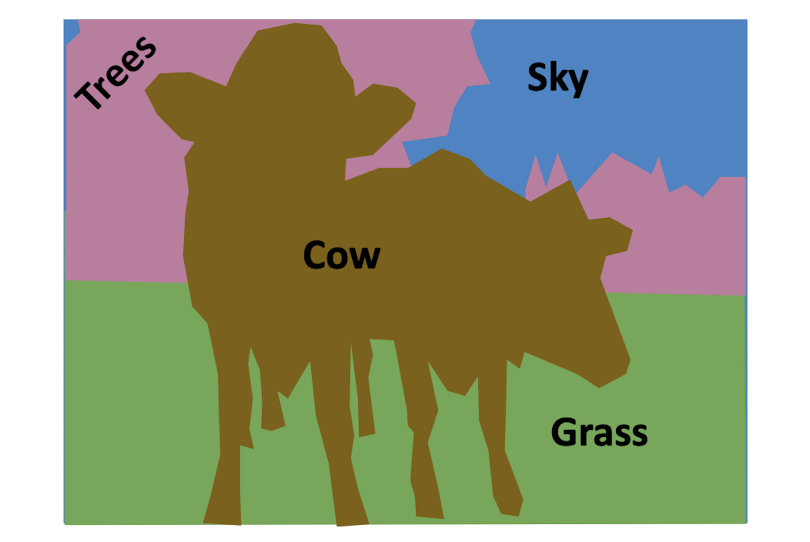Things 와 Stuff 구분하지 않고 모든 픽셀을 라벨링하는 것을 목표로함 instance를 구별하지 않는다 (ex 소가 2마리인지 - (X) )

Train Data

X : 원본 image
Y : 모든 pixel에 대해 labeling 된 이미지 (GT)

f( pixel ) → pixel category

---

Method

1. Sliding Window

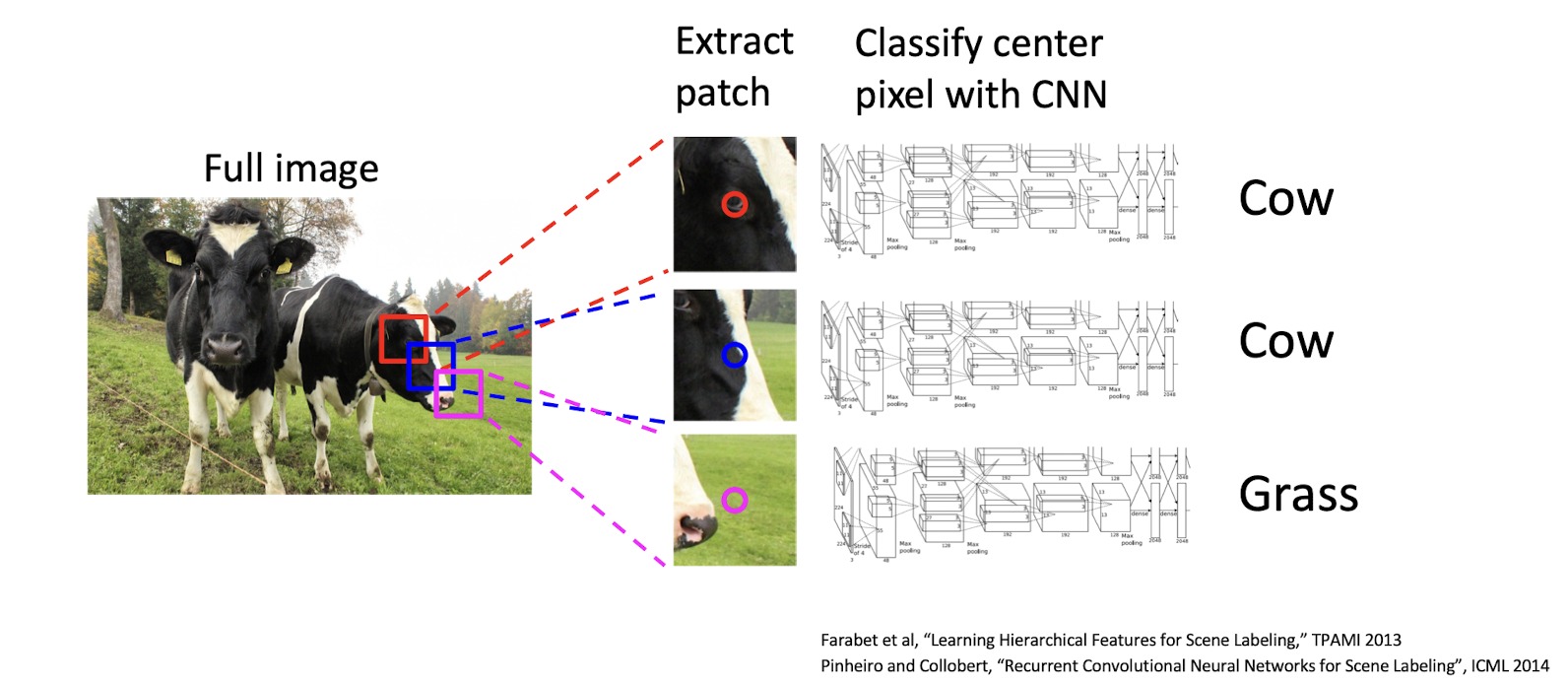
• pixel → pixel의 카테고리
  • 특정 pixel 에 대해 labeling을 하려면 주변 정보가 필요함 → patch
  • 해당 pixel을 중심으로 한 image patch를 뽑아낸다. → patch를 CNN에 돌려서 classify
• 👎
  • 연산량 많고 중복되는 연산도 너무 많음
  • 한 칸씩 옮겨가며 각 pixel에 대해 cnn 돌리면 패치끼리 겹치는게 넘 많음
  • Test시 매우 느림 : train시엔 픽셀을 샘플링해서 배치를 만들면 시간을 효율적인 학습 가능! BUT 여전히 test 시에는 이미지를 생성해야하기 때문에 모든 픽셀에 대해 연산 수행해야함

2. CNN + classification head

👎 : CNN을 태우면 이미지 크기가 작아짐 (stride, pooling)

즉, output을 input 크기로 낼 수 없다

3. FCN : Fully Convolution Network

input size = output size 을 위한 두 가지 approach

IDEA 1

• No Fully Connected Layers, (위치정보가 사라지므로)
• Pooling Layers (할수록 해상도가 작아져서, 원본이랑 같은 크기의 output을 만들 수 없음)
• Only Convolution blocks

input의 사이즈를 보존하는 CNN을 설계

• 👎
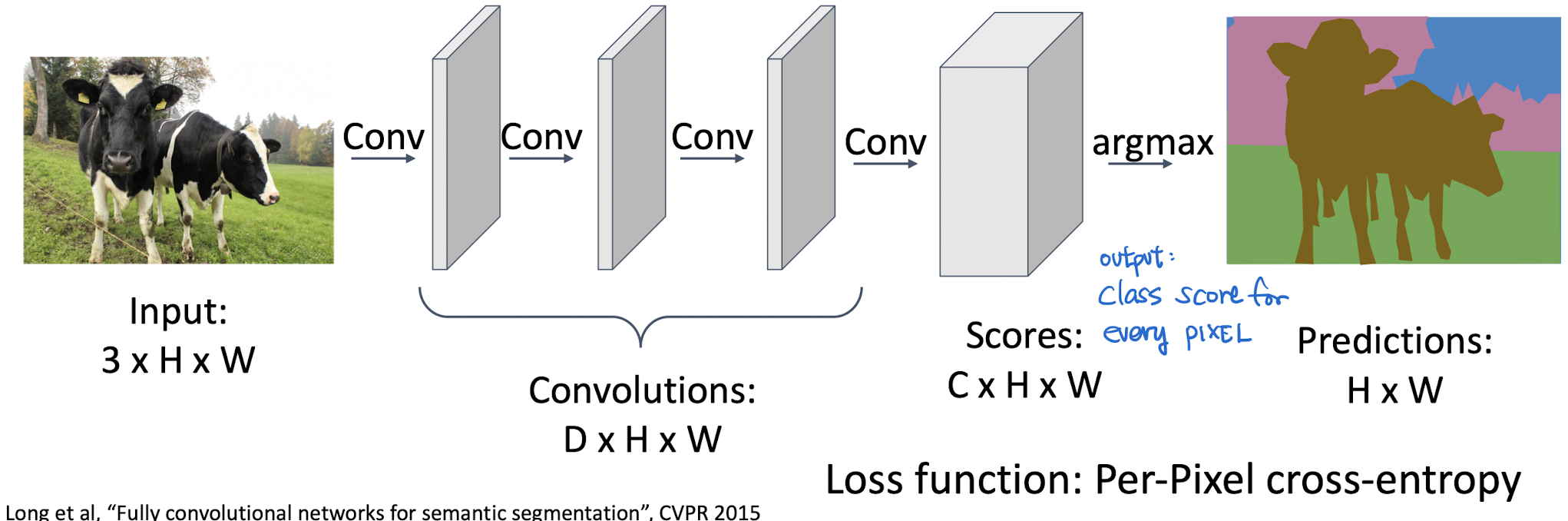
  • 연산량이 너무 많다. backprop시 연산량 많음
    • 마지막 레이어에서의 한 픽셀은, 앞 layer의 넓은 영역을 보게 되어있었음. 뒷쪽(몇 안되는 픽셀)에서 loss가 오면 backprop를 진행했음. but 뒷쪽까지 같은 사이즈면 하나 업뎃을 하기 위해 엄청난 양의 계산이 필요함
  • receptive field size (= ConvNet feature가 바라보고 있는 input의 영역)
    • Pixel 수준에서의 Classification를 잘하기 위해서는 High-level semantic features 와 Large receptive fields가 필요하다.
    • 이미지 전체를 보기 위해서, FC layer를 연결하거나 Pooling을 하는 방법이 있는데, FC layer는 위치정보를 잃어서 부적합 + Pooling 은 할수록 output 사이즈가 작아져서 원본 size를 보존할 수 없다는 문제가 있다. https://peng-hi.tistory.com/5
      

IDEA 2 : Encoder-Decoder Network (Deconvolution Network)

Design a Network with only Conv layers with downsampling + upsampling layers

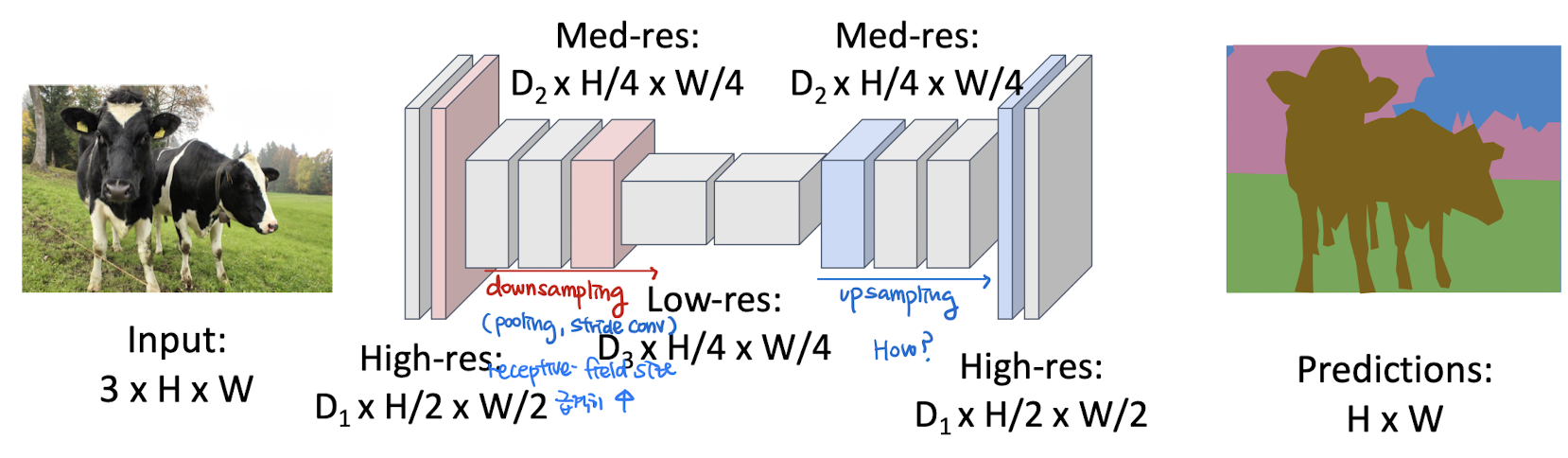
Downsampling

stride / max-pooling

Upsampling

• Nearest Neighbor

  주변을 다 같은 값으로 채워버린다

  

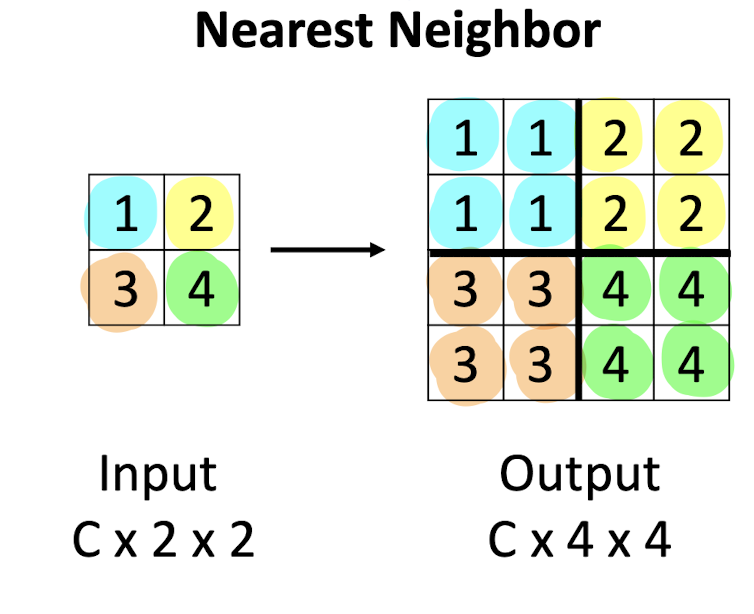
• Bed of Nails

  max 값 하나 남겨서 (위치 고정) 해놓고, 나머지 자리는 0으로 채운다.
  
  

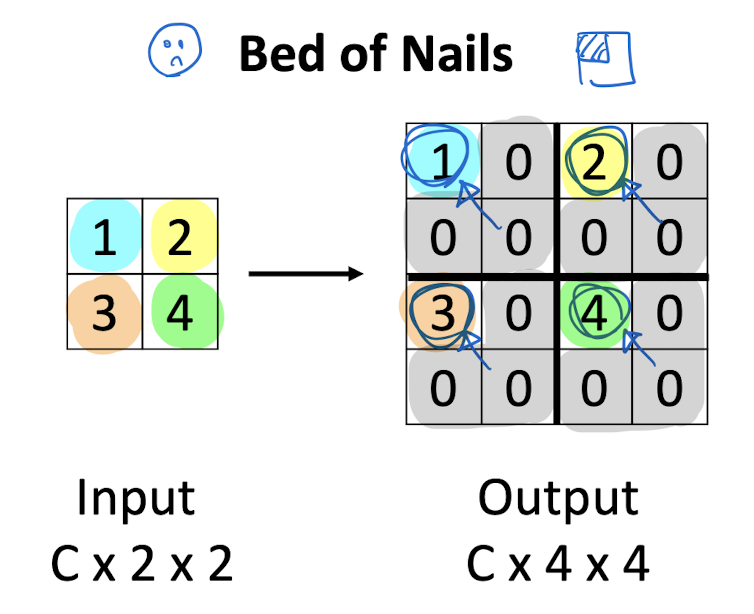
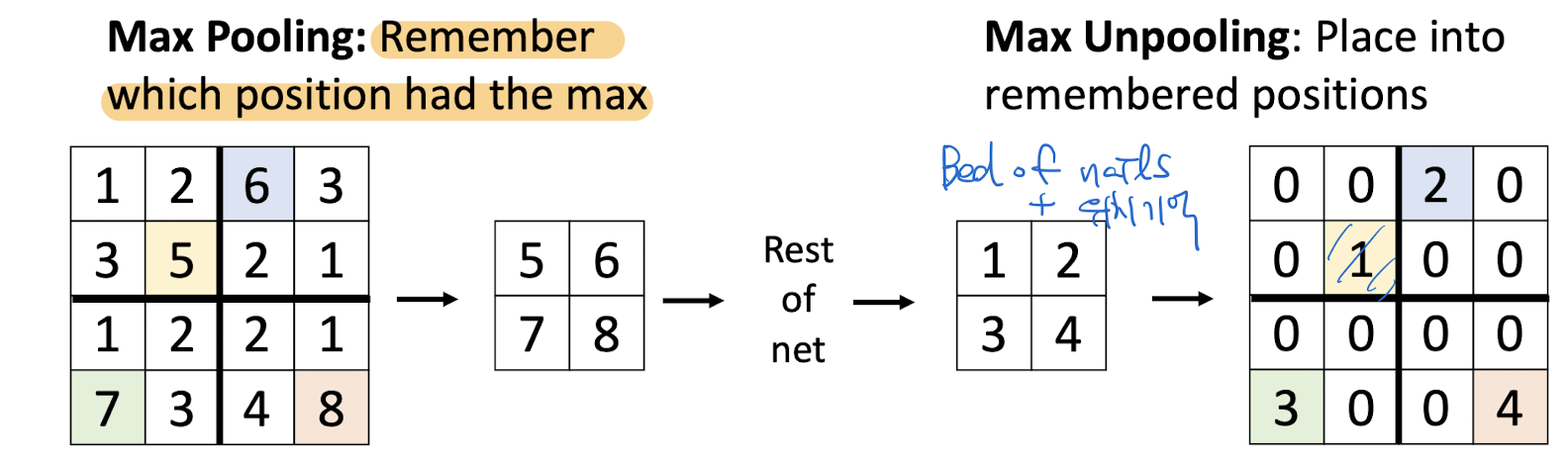
• Max Unpooling

  max값의 위치를 기억하고 있다가, 위치대로 쓰고 나머지는 0 padding
  

• Transpose Convolution - learnable upsampling

  • Recall : Convolution을 활용한 downsampling

    Picking up things in the corresponding region (주워담기)
    

  • Deconvolution (stamping!) = Transpose Convolution
    

    Deconvolution : 수학적 관점 = Transpose Convolution

  • conv-deconv 관계

    그림으로 봤을 때는 : 역연산!

    행렬으로 봤을 때는 : transpose!

• Bilinear Interpolation

• Bicubic interpolation

• Dilated (Atrous) Convolution