선형 레이어 Linear Layer는 Dense Layer, Fully Connected Layer 등등 다양한 이름으로 불려진다.
linear layer는 선형 변환을 활용하여 데이터를 특정 차원으로 변환하는 기능을 한다.
100차원의 데이터를 300차원으로 변환한다면 데이터를 더 풍부하게 표현하는 효과를 가질 것이고,
100차원의 데이터를 10차원으로 변환한다면 데이터를 집약시키는 효과를 가질 것이다.
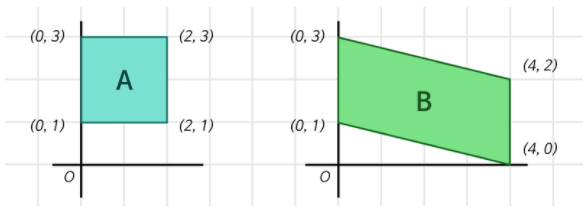
점 4개로 2차원을 표현하므로 각각 (4,2) 행렬 형태의 데이터로 표현할 수 있다.
두 사각형의 데이터를 집약시켜 각각 어떤 하나의 정수로 표현하고자한다.
1단계 : (4,2) x (2,1)행렬 = (4,)
2단계 : (4,) x (4,1)행렬 = (1,)
2차원을 1차원으로 변환하는데 (2,1) 행렬이 하나 선언되고,
4차원을 1차원으로 변환하는데 (4,1) 행렬이 하나 선언된다.
linear layer는 (입력차원,출력차원)에 해당하는 weight를 가지는 특성을 가진다.
즉, 각각의 행렬들이 레이어의 weight이다.

두 사각형에 대해 1단계를 거치고 난 뒤의 결과가 동일하여 2단계의 (4,1) weight를 거치는 것이 의미가 없어진다. 문제를 해결하기 위해 데이터를 집약시키는데 집중했는데 실패하였으니 이번에는 데이터를 더 풍부하게 만들어보자.
1단계 : (4,2) x (2,3)행렬 = (4,3)
2단계 : (4,3) x (3,1)행렬 = (4,)
3단계 : (4,) x (4,1)행렬 = (1,)

1단계를 통해서 각 사각형에 대한 독립적인 정보를 생성하여 사각형을 구분할 수 있게 되었다.
그렇다면 위의 식에서 몇 개의 parameter가 사용되었을까?
1단계 : 23=6
2단계 : 31=3
3단계 : 4*1=4
총 13개의 파라미터가 사용되었다.
우리가 weight의 형태만 선언해주면 파라미터값은 임의로 채워지고 가장 적합한 weight를 찾아가는 과정이 바로 training이다 😲 파라미터가 많으면 좋긴하지만, 지나치게 많은 파라미터는 overfitting을 야기한다.
y = Wx+b
추가로 편향(bias)에 대해서 말해보자면
선형변환된 값에 편향 파라미터를 더해주므로써 (평행이동) 두 데이터를 일치시킬 수 있다.