time complexity
복잡도 분석
알고리즘을 푸는데있어서 시간과 공간을 얼마나 차지하는지 나타내는 지표이다.
시간과 공간의 복잡도가 곧 효율성을 나타낸다.
알고리즘은 일단 성능을 내는게 중요하지만 그 다음으로는 그 효울을 따져 알고리즘을 평가한다고 할수있다.
Big - O
알고리즘의 성능을 수학적으로 표현해주는 표기법
알고리즘의 시간과 공간 복잡도를 표현할수 있다
O(1) : constant time
입력데이터의 크기의 상관없이 언제나 일정한 시간이 걸리는 알고리즘을 표현한다.
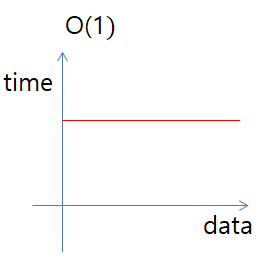
데이터가 증가해도 성능의 변함이없음을 볼수있다.
O(n) : linear time
입력데이터 크기에 비례해서 처리시간이 걸리는 알고리즘을 표현한다.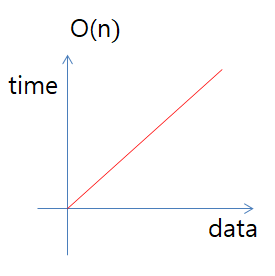
데이터가 증가함에 따라 처리시간도 같이 증가하고있다.
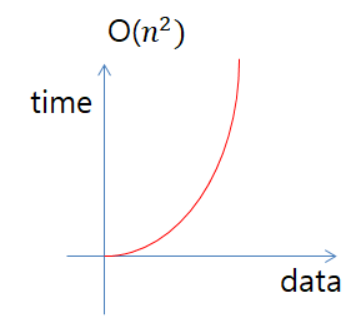
O(n^2) : Quadratic time
첫번째 Loop 에서 n번 돌면서 각각의 엘리먼트에서 n 번씩 또 돌기때문에 처리횟수가 n을 가로 세로 길이로 가지는 면적만큼추가된다. n이하나 늘어날때마다 n만큼식 계속해서 생성되기때문에 데이터가 커지면 커질수록 처리시간이 크게 늘어난다.
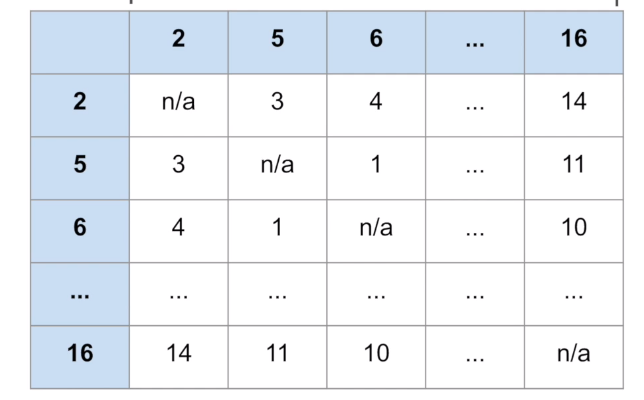
O(nm) : Quadratic time - 2
O(n^2)표기법과 비슷하지만 해당 표기법은 변수가 다르다면 빅O가 표기법에도 반드시 다르게 표현하여야 한다.
O(n^3) : (polynomial / cubic time)
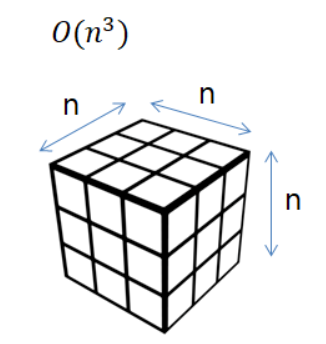
O(n)일 경우에는 직선이고 O(n^2)이면 면적이된다. 그리고 O(n^3)이면 n의 제곱을 n만큼 더 돌리니까 큐빅모양이 될 것이다.
O(2^n) : Fibonacci (Exponential Time)
데이터의 증가에따라 처리시간이 현저히 늘어난다.
출처: https://bkjeon1614.tistory.com/25 [아무거나]
FrontEnd Developer