한 문장으로 정리하는 computer vision (1)

CS231N, EECS 498-007 / 598-005에서 나타나는 개념을 정리하기 위하여 복기 용도로 작성하였습니다.
간단히 정리한 내용을 살펴보며 모르는 부분이 있을 때 찾아보는 용도로 보시면 좋을 것 같습니다.

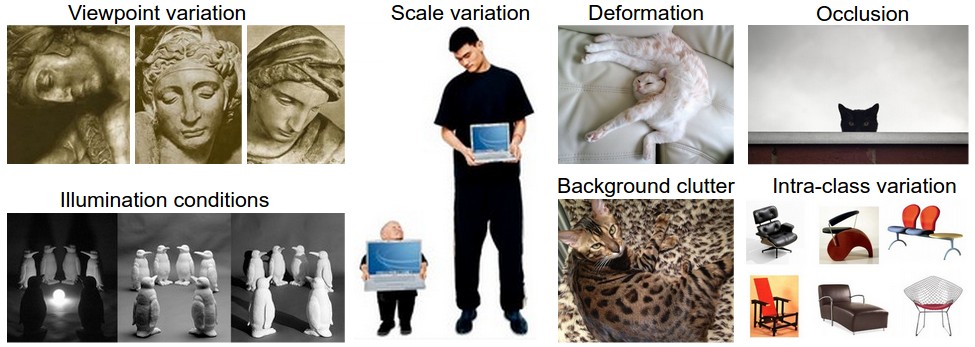
이미지 분류 challenges

1. Viewpoint variation
동일한 객체라도 카메라의 각도에 따라 달르게 인식 될 수 있다.
2. Scale variation
동일한 객체라도 객체의 크기가 일정하지 않다.
3. Occlusion
객체의 일부분만 표시되어 나타날 수 있다.
4. Illumination conditions
조명의 변화는 픽셀의 변화가 급격하게 나타난다.
5. Background clutter
복잡한 배경이 객체와 섞일 수 있다.
6. Intra-class variation
객체의 변화 및 범주가 넓을 수 있다.

---

K-Nearest Neighbor Classifier

• 개념
  새로운 데이터를 기존의 데이터와의 거리를 측정하여 가장 가까운 K개의 이웃(데이터)을 바탕으로 예측한다.
• 특징
  1. non-parametric algorithm
     주어진 모델이 데이터가 확률분포를 기반으로 모수(parametic)를 추정하는 과정이 없다.
  2. lazy learner algorithm
     학습 세트에서 즉시 학습하지 않고 데이터 세트를 저장하고 분류시 데이터 세트에 대한 작업을 수행한다.
  3. hyperparameters
     • 거리지표
       • L1 distance 축 방향의 거리를 모두 종합한 수치(Manhattan Distance, 강의에서는 이미지 데이터 I의 픽셀 p 거리를 모두 종합함)
         $d_1(I_1,I_2)=\sum_{p} |I^p_1-I^p_2|$
       • L2 distance 관측치의 방향 최단거리(직선)을 종합한 수치(Euclidean Distance)
         $d_1(I_1,I_2)= \sqrt{\sum_{p} (|I^p_1-I^p_2|)^2}$
     • K
       값이 작을경우 모델이 overfitting, 클 경우 과하게 정규화 underfitting 한다.
  4. 조합방법
     이웃의 갯수가 같은 경우 거리가 가까운 경우 가중치를 두는 형식으로 해결 할 수 있다.
  5. 장,단점
     • 구현하고 이해하는 것이 매우 간단하다.
     • 학습 데이터를 저장하고 인덱싱하기 만하면되기 때문에 분류기는 학습에 시간이 걸리지 않습니다.
     • 테스트 단계에서 모든 학습데이터와 거리를 측정하므로 시간이 오래걸린다.
     • 최적의 K값 설정이 데이터의 특성에 따라 달라진다.
     • 데이터가 저차 원인 경우 좋은 선택 일 수 있지만 실제 이미지 분류에서 사용하기에는 적합하지 않다.

---

Cross-validation

• 단계
  1. train set를 train set와 validtaion set으로 설정합니다.
  2. validation set을 사용하여 모든 hyperparameter를 조정합니다.
  3. test set에서 한 번 실행하고 성능을 확인합니다.
• 특징
  - hyperparameter 수가 많은 경우 큰 validation split을 사용하는 것이 좋습니다.
  - validation set의 수가 적으면 Cross-validation 검사를 사용하는 것이 더 안전합니다.
  - 실제로 볼 수있는 일반적인 폴드 수는 3 배, 5 배 또는 10 배 교차 검증입니다.
  - fold를 순차적으로 validation으로 설정하여 반복하고 성능을 평가 한 다음 마지막으로 각 fold들의 성능을 평균화합니다.
  

---

참고자료

cs231n 강의 자료
cs231n 한글 강의 자료
EECS 498-007 / 598-005 2019 강의 자료
KNN 한글설명