한 문장으로 정리하는 computer vision (2)

CS231N, EECS 498-007 / 598-005에서 나타나는 개념을 정리하기 위하여 복기용도로 작성하였습니다.
간단히 정리한 내용을 살펴보며 모르는 부분이 있을 때 찾아보는 용도로 보시면 좋을 것 같습니다.

score function

• raw data를 class scores로 변환하는 함수

loss function

• ground truth labels과 predicted scores과의 차이를 정량화 한것으로 높이거나 낮추는 방식으로 optimization 한다. (동의어 cost function, objective function)

Linear classifier

• $f(x_i,W,b)=Wx_i+b$
• image $x_i$ : 모든 pixels이 평평하게(flattened) 되어 단일 column vector 로 표현한다(shape은 [D x 1])
• The matrix $W$ ([K x D]), 그리고 vector $b$ ([K x 1])은 함수의 매개 변수(parameters)이다.
• CIFAR-10에서, $x_i$는 i번째 image의 모든 픽셀으로 크기는[3072 x 1]이며, W는 [10 x 3072] and $b$는 [10 x 1]이다, 따라서 3072숫자(the raw pixel values)들은 함수를 통과하여 10개(the class scores)의 숫자로 표현된다.
• parameters $W$는 weights으로, $b$는 bias vector으로 표현한다.
• 주의사항
  • 한 번의 matrix multiplication인 $Wx_i$ 만으로 10 개의 다른 classifiers(각 클래스마다 하나씩)를 병렬로 계산하는 효과. 이 때 $W$ 행렬의 각 열이 각각 하나의 classifiers가 된다.
  • KNN과 달리, 학습 데이터가 파라미터들인 $W$, $b$ 를 학습하는데 사용되지만 학습이 끝난 이후에는 학습된 파라미터들만 남기고, 학습에 사용된 데이터셋은 더 이상 필요가 없다는 (따라서 메모리에서 지워버려도 된다는) 점이다. 그 이유는, 새로운 테스트 이미지가 입력으로 들어올 때 위의 함수에 의해 스코어를 계산하고, 계산된 스코어를 통해 바로 분류되기 때문이다.

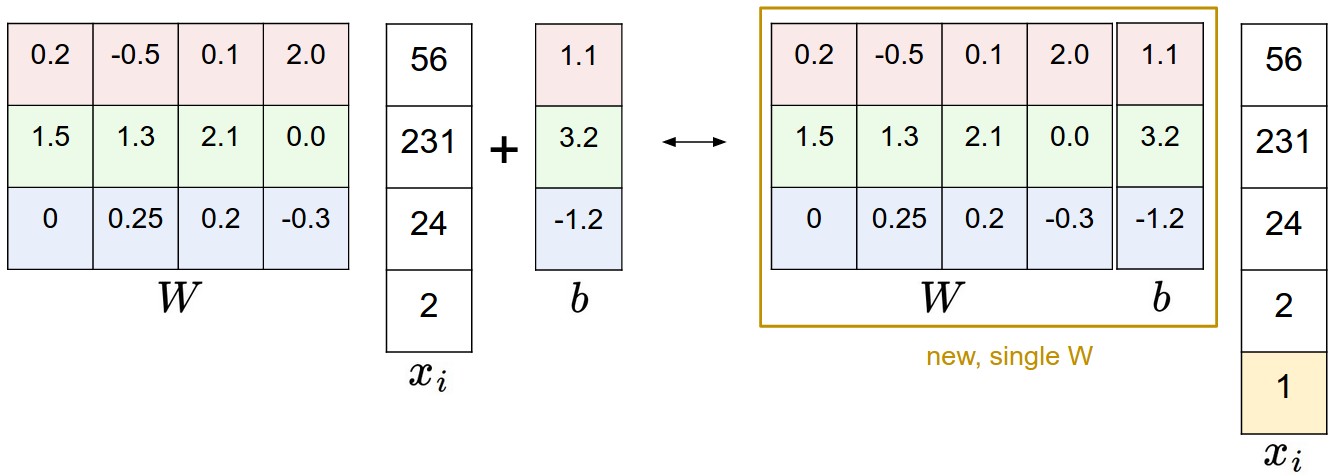
Bias trick

• $f(x_i,W,b)=Wx_i+b$ 에서
• $f(x_i,W)=Wx_i$ 으로
• 두 가지 파라미터를 (bias $b$와 weight $W$) 매번 동시에 고려해야 한다면 표현이 번거로워진다. 흔히 사용하는 트릭은 이 두 파라미터들을 하나의 행렬로 합치고, $x_i$를 항상 $1$의 값을 갖는 한 차원(디폴트 bias 차원)을 늘리는 방식이다. 이 한 차원 추가하는 것으로, 새 스코어 함수는 행렬곱 한 번으로 계산이 가능해진다
  

Multiclass Support Vector Machine (SVM) loss

• The SVM loss는 각 이미지의 correct class 점수가 incorrect classes보다 일정수치(fixed margin $\Delta$) 이상이기를 원하는 손실 함수이다.
• i번째 image 픽셀 값인 $x_i$와 the label $y_i$는 해당 이미지의 올바른 class 값이다.
• score function은 픽셀값으로 클래스 점수 값인 벡터 $f(x_i,W)$을 계산한다. (이는 s값으로 요약하여 표기함, score를 축약함). j번째 클래스의 점수 값은: $s_j=f(x_i,W)_j$.
• Multiclass SVM의 loss for the i번째 예제의 로스 값은 다음과 같다
  $L_i=\sum_{j\neq y_i} max(0, s_j-s_i+\Delta)$
• hinge loss
  • 0에서 임계값(threshold)을 갖는 함수: $max(0,−)$를 hinge loss라고 합니다.
  • squared hinge loss SVM (or L2-SVM)는 $max(0,−)^2$으로 나타내며 margin에 강력한 패널티를 부과하고자 할때 사용 합니다.
    

Regularization

• 최적의 score를 가지는 parameter가 여러가지 일 경우 로스 함수를 수정하여 regularization penalty$R(W)$를 줄 수 있습니다.
• 가장 일반적인 regularization penalty는 L2 norm으로 (large weights를 비선호discourages하는 방향) 모든 parameter에 elementwise quadratic penalty를
  부과합니다.
  $R(W)=\sum_k\sum_l W_{k,l}^2$
• full Multiclass Support Vector Machine loss는 data loss과 regularization loss으로 구성되며 아래와 같습니다.
  $L = \underbrace{ \frac{1}{N} \sum_i L_i }_\text{data loss} + \underbrace{ \lambda R(W) }_\text{regularization loss} \\\\$
• regularization penalty를 loss objective에 추가했으며, hyperparameter λ에 의하여 가중됩니다. 이 λ를 설정하는 간단한 방법은 없으며 대부분 cross-validation에서 결정됩니다. 풀어쓴 식은 아래와 같습니다.
  $L = \frac{1}{N} \sum_i \sum_{j\neq y_i} \left[ \max(0, f(x_i; W)_j - f(x_i; W)_{y_i} + \Delta) \right] + \lambda \sum_k\sum_l W_{k,l}^2$
• Setting Delta
  • $\Delta$와 λ가 별개의 hyperparameter으로 보이지만 사실상 같은 역할의 tradeoff(data loss and the regularization loss)를 지니고 있습니다.
  • W의 값을 줄인다면 점수 차이가 작아지며(data loss커짐 & regularization loss작아짐), 값을 늘인다면 점수 차이가 커집니다(data loss작아짐 & regularization loss커짐).
  • 따라서 정확한 $\Delta$설정에는 의미가 없으며), 실제 값 조정의 tradeoff는 weights가 증가하도록 허용하는 크기입니다 (regularization strength λ를 통해).

Softmax classifier

• function mapping: $f(x_i; W) = W x_i$은 변함없지만, 이 scores는 각 class에 대하여 unnormalized log probabilities으로 해석하여, hinge loss를 cross-entropy loss 으로 변환합니다:
  $L_i = -\log\left(\frac{e^{f_{y_i}}}{ \sum_j e^{f_j} }\right) \hspace{0.5in} \text{or equivalently} \hspace{0.5in} L_i = -f_{y_i} + \log\sum_j e^{f_j}$
• $f_j(z) = \frac{e^{z_j}}{\sum_k e^{z_k}}$은 softmax function으로: 임의의 실수 scores(z)로 구성된 벡터를 취하여 합계가 1 인 0과 1 사이의 값 벡터로 squashes합니다.

• Information theory view

  • “실제” 분포 p와 추정 분포 q사이의 cross-entropy는 다음과 같이 정의됩니다:
    $H(p,q) = - \sum_x p(x) \log q(x)$
  • Softmax classifier는 추정 된 클래스 확률 (위에서 볼 수있는 $q = e^{f_{y_i}} / \sum_j e^{f_j}$)과 "실제"분포 사이의 cross-entropy를 최소화합니다.
  • 실제 분포 엔트로피는 아래와 같이 표시할 수 있습니다: $H(p) = -\sum_{x} p(x)\log p(x)$,
    강의 교재에서는 all probability mass is on the correct class (i.e. p=[0,…1,…,0] contains a single 1 at the yi -th position.)으로 규정했습니다.
  • cross-entropy는 entropy와 Kullback-Leibler divergence(KL 발산)의 관점에서 $H(p,q) = H(p) + D_{KL}(p||q)$와 같이 쓸 수 있고 델타 함수 $p$의 엔트로피는 0과 같습니다. 그러므로 두 분포 사이의 KL 발산을 최소화하는 것과 동일합니다.

• Probabilistic interpretation

  • $P(y_i \mid x_i; W) = \frac{e^{f_{y_i}}}{\sum_j e^{f_j} }$는 이미지 $x_i$가 $W$에 의해 parameterized했을때 올바른 label $y_i$가 나타날 (normalized, 정규화된) 확률로 볼수 있다.
  • Softmax classifier는 output vector 내부에 있는 점수 $f$를 unnormalized log probabilities으로 해석합니다. 이를 Exponentiating 하며, 나누기는 normalization 역할을 수행하여 합산했을때 1이 나타납니다.
  • likelihood function(단순히 likelihood으로도 표현)은 알려지지 않은 parameters가 주어졌을때, 이 값에 대한 데이터 샘플이 통계 모델의 적합한가를 측정합니다. (likelihood와 pdf|pmf 관련 함수 notation과 순서 주의)
  • 확률론적 관점에서, negative log likelihood of the correct class를 minimizing하고 있으며 이는 Maximum Likelihood Estimation (MLE)를 수행하는 것과 같습니다.
    + MLE에서 MAP를 적용하기 위해서는 Prior정보를 알고 있어야하는데, 이를 weight W에 대해 Gaussian Distribution를 L2정규화를 적용하는것으로(평균을 0으로 하여 값을 적게 설정하는 정규화 방식) 설정하여 해석이 가능하다. 참고

• Numeric stability

  • $e^{f_{y_i}}$ 와 $∑_je^{f_j}$가 exponentials을 취해서 굉장히 커질 수 있다. 큰수를 나누는것은 불장언하기 때문에 normalization trick을 사용한다.
  • 분수의 분모와 분자에 상수 constant C를 곱하며, C값은 $\log C=−\max_jf_j$으로 보통 설정한다.단순히 가장큰 값을 0으로 shift한 효과이다.
    $\frac{e^{f_{y_i}}}{\sum_j e^{f_j}} = \frac{Ce^{f_{y_i}}}{C\sum_j e^{f_j}} = \frac{e^{f_{y_i} + \log C}}{\sum_j e^{f_j + \log C}}$

SVM vs. Softmax

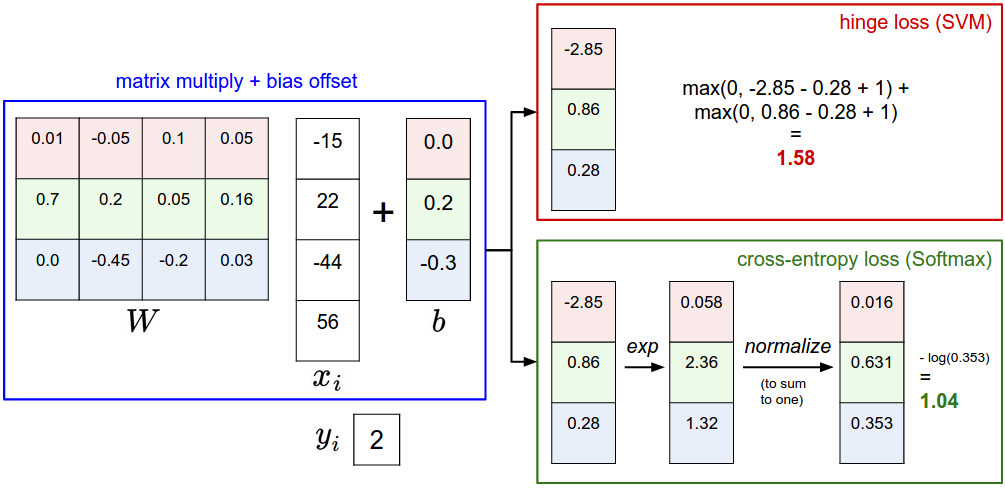
• SVM은 score vector f를 class score로 보고 loss function은 correct class가 나머지 스코어 점수보다 margin이상의 점수를 갖도록 장려합니다.
• Softmax는 scores를 각 class에 대한 (unnormalized) log probabilities로 해석하고 correct class에 대한 (normalized) log probability가 높은 점수를 갖도록 장려합니다.
• SVM은 값이 일정 수준이상으로 만족하면 개선하고자 하지 않지만, softmax는 나머지 확률이 0인 원핫 형태가 될때까지 개선하고자 합니다.

---

강의 중 질문 정리

SVM

Q1: What happens to loss if car scores decrease by 0.5 for this training example?
correct class의 score가 margin이상의 범위를 유지한다면, 값이 아무리 크게 변하더라도 로스값은 변함없다.

Q2: what is the min/max possible SVM loss Li?
0~inf

Q3: At initialization W is small so all s ≈ 0. What is the loss Li, assuming N examples and C classes?
C-1= (C-1)*(margin - 0)

Q4: What if the sum was over all classes? (including j = y_i)
현 loss + 1(margin)

Q5: What if we used mean instead of sum?
loss=loss/(C-1), 최악/평균 로스값 알고 있다면 디버깅시 유용함

Q6: What if we used 제곱?
penalizes violated margins more strongly (quadratically instead of linearly).

Q7: Suppose that we found a W such that L = 0. Is this W unique?
아님, 2W도 가능, W vs W2? regularitaion로 선택

Soft max

Q1: What is the min/max possible softmax loss Li?
0~inf( 0되는건 사실상 불가능 되려면 정확히 원핫형식으로 나타나야함)

Q2: At initialization all sj will be approximately equal; what is the softmax loss Li, assuming C classes?
A: -log(1/C) = log(C), If C = 10, then Li = log(10) ≈ 2.3, 디버깅시 유용하게 사용

---

SVM https://ratsgo.github.io/machine%20learning/2017/05/23/SVM/
정보이론 https://3months.tistory.com/436
cross-entropy https://towardsdatascience.com/cross-entropy-loss-function-f38c4ec8643e
MLE>MAP 유도 https://hyeongminlee.github.io/post/bnn002_mle_map/
확률 이론 http://sanghyukchun.github.io/58/