한 문장으로 정리하는 computer vision (4)

CS231N, EECS 498-007 / 598-005에서 나타나는 개념을 정리하기 위하여 복기용도로 작성하였습니다.
간단히 정리한 내용을 살펴보며 모르는 부분이 있을 때 찾아보는 용도로 보시면 좋을 것 같습니다.

Linear Classifiers 문제점

• Geometric Viewpoint
  군집형태는 분류가 불가능하다
• Visual Viewpoint
  클래스 당 하나의 템플릿만 가질 수 있기때문에, 실제로 같은 class여도 정해진 템플릿과 비슷한 생김새가 아니라면 그 class로 인식될 수 없게 된다.

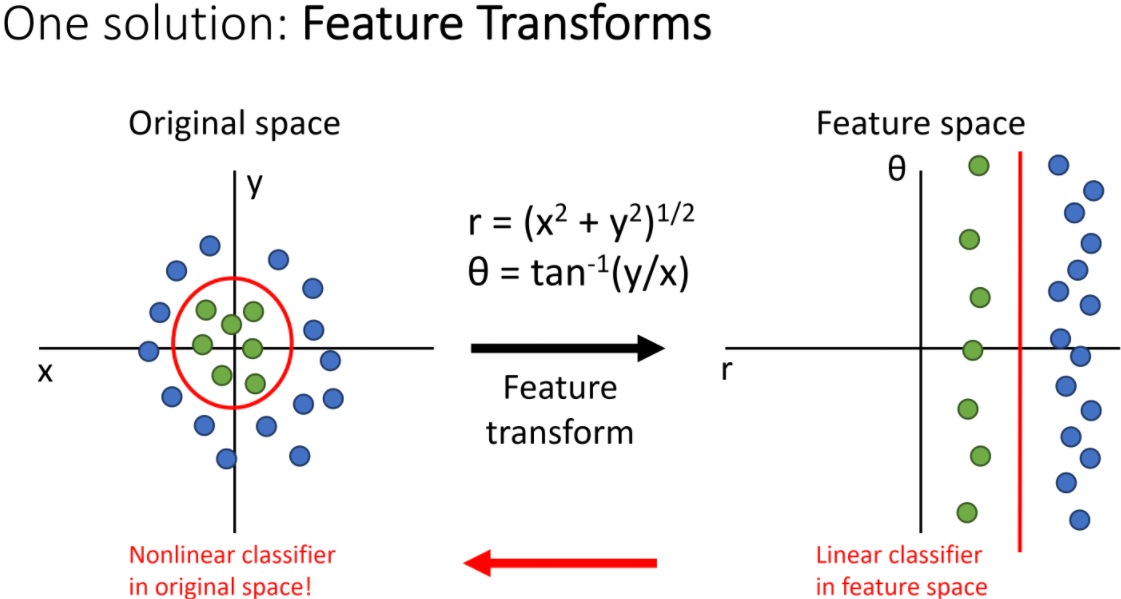
Feature Transforms

• 특징
  non linear decision boundary를 linear Classifiers가 구분가능하게 변화시킬 수 있다.
• 조건:
  • 데이터의 형태를 파악하고 있어야 한다.
  • 데이터에 맞는 feature transform을 알고 있어야 한다.
• 한계
  • 실 데이터는 고차원 상에 있고, 데이터가 어떻게 분포하고 있는지 전혀 모른다.
  • linear decision boundary를 가졌을 때, 가장 분류가 잘 되게 하기 위해서 어떻게 변환을 할 지도 알 기 어렵다.

Color Histogram

• RGB를 스펙트럼화
• Pixel(3072개)들이 각각 어느 color 스펙트럼에 속해있는지 확인한다.
• Pixel들의 컬러 분포를 히스토그램으로 표현한다.

Histogram of Oriented Gradients (HoG)

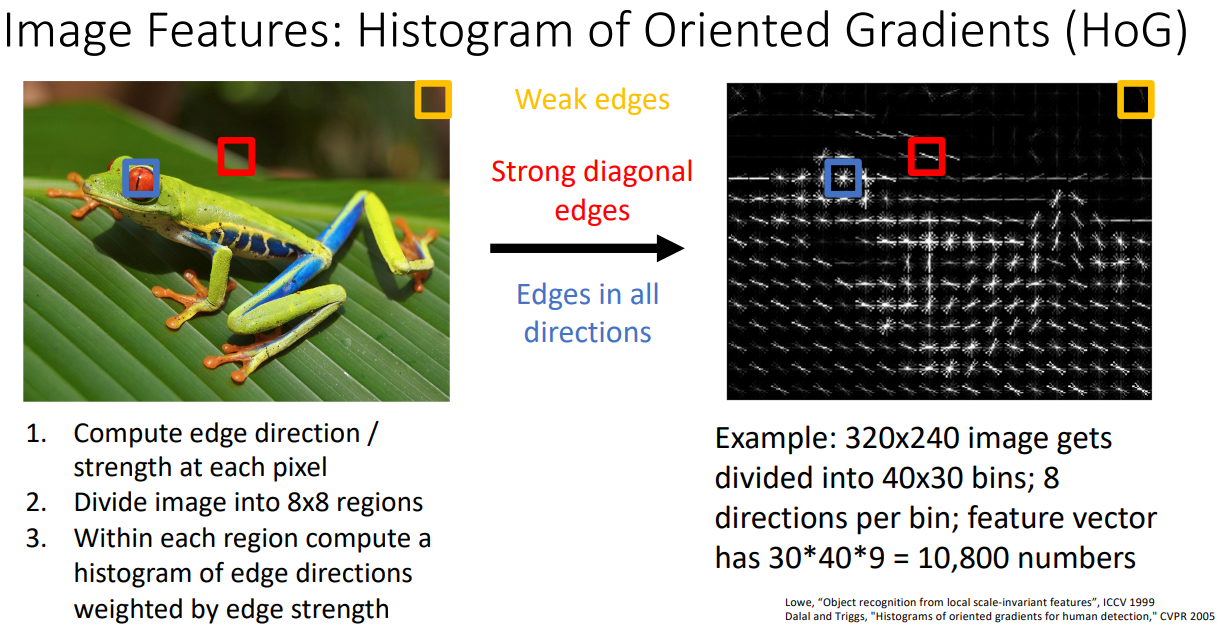
• 순서
  1. edge의 방향과 크기를 픽셀단위로 계산한다.
  2. 이미지를 8*8 크기의 region으로 나누어준다.
  3. 각 region내에서 edge의 방향과 크기를 histogram형식으로 계산한다.
• 특성
  • 작은이미지 단위에서 edge들의 방향과 크기를 살펴 볼 수 있다.

Image Features: Bag of Words (Data-Driven!)

• 순서
  1. 이미지의 patches를 다양한 크기로 잘게 나눈뒤 각각에 PCA등을 적용하여, dictionary 형태의 patches를 클러스터형식으로 구성한다.(codebook 혹은 visual words)
  2. 사전에 정의된 codebook에 해당하는 patches들을 히스토그램 형식으로 인코딩합니다.

Image Feature vs Neural Networks

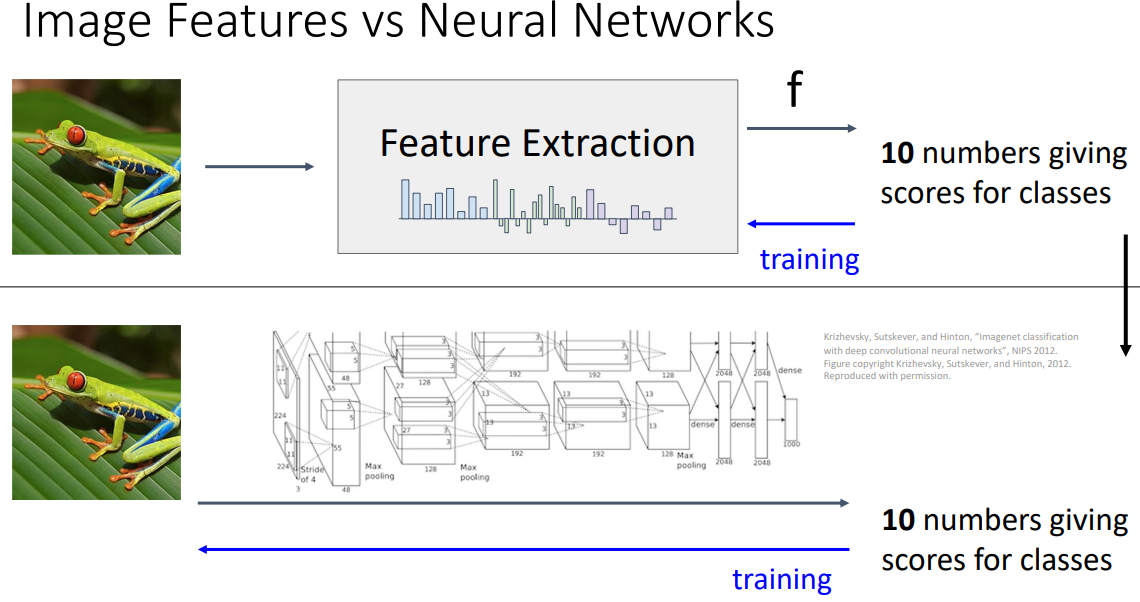
• 이미지에 특성을 추출한 다음 피쳐를 종합하는 방식을 학습하는 것이었지만
  (뉴럴 넷에서는)피쳐 추출과정과 분류과정을 모두 학습하는 방식으로 변화했다.

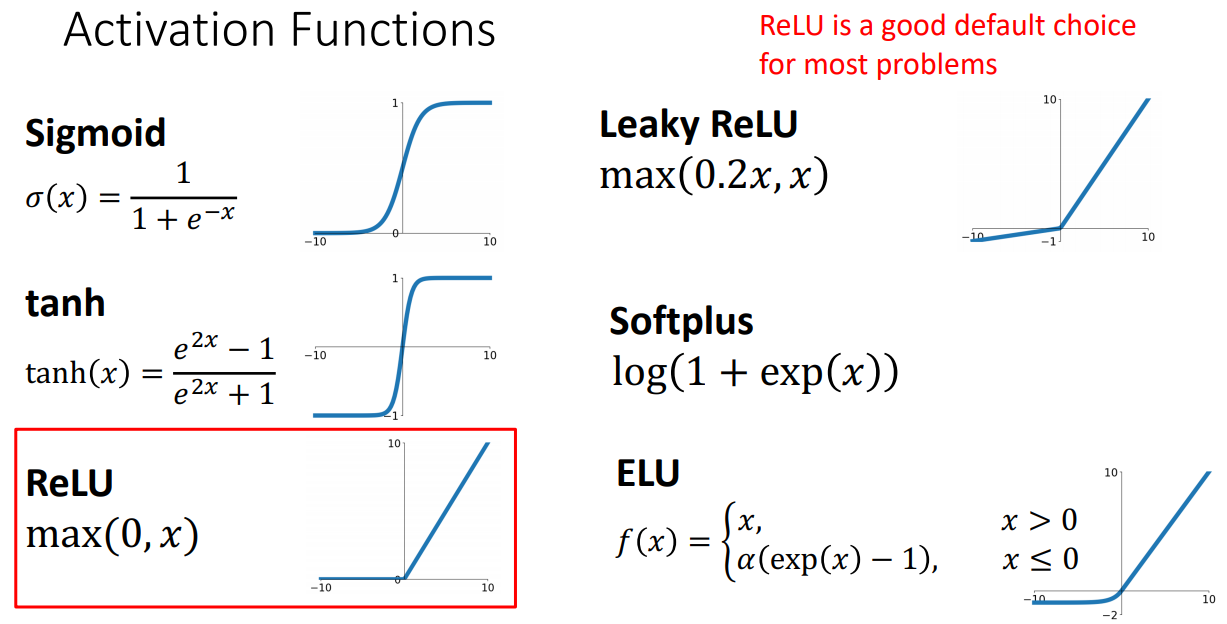
Activation function

• 종류
  
• 질문
  Q: What happens if we build a neural network with no activation function?
  A: We end up with a linear classifier!(결국 선형 분류기가 됨)
  linear classifier의 한계를 넘기위해 activation function을 사용한다.
  activation function 사용시: $f(x)=W_2\max(0,W_1x+b_1)+b_2$
  activation function 미 사용시: $f(x)=W_2(W_1x+b_1)+b_2=(W_1W_2)x+(W_2b_1+b_2)$
• 예시
  
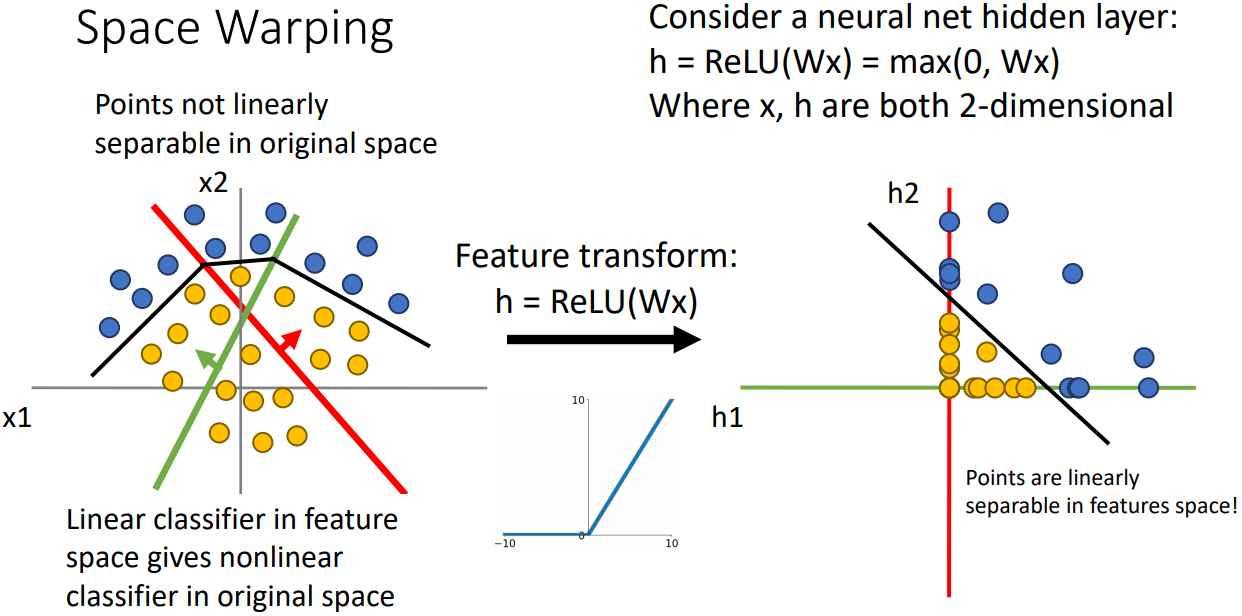
  1. feature transform: x1과x2로 구성된 좌표계가 초록색과 빨간색이 새로운 축인 선형변환을 시도한다.
  2. 변환된 각 좌표계에서 양수인부분은 유지되며 음수인경우 0이되는 ReLU를 적용하면 음의 좌표를 갖는 점들이 축에 “collapsed”된다.
  3. 오른쪽 그림에서 점들이 linearly separable 된다. (ReLU를 적용하지 않으면 왼쪽 그림처럼 non-linearly separable함)
  4. hidden units(layer)가 많아지면 overfit하는 경향이 있지만 이를 해결하기위해 hidden units의 크기나 층을 줄이지 않고 정규화 값($\lambda$)을 크게 주어 조절한다.

Convex functions

• convex fuction은 bowl형태를 띄고 있고 global minimum를 가지고 있어 최적화 하기 쉽다.
• neural network의 loss function이 convex 하다고 가정하여 최적화를 진행한다.
• 하지만 대부분 neural network은 nonconvex optimization을 해야하며 수렴의 보장을 할 수 없다.

참고자료

cs231n 강의 자료
cs231n 한글 강의 자료
EECS 498-007 / 598-005 2019 강의 자료
convnet 데모