CS231N, EECS 498-007 / 598-005에서 나타나는 개념을 정리하기 위하여 복기용도로 작성하였습니다.
간단히 정리한 내용을 살펴보며 모르는 부분이 있을 때 찾아보는 용도로 보시면 좋을 것 같습니다.
Simple expressions and interpretation of the gradient
- x와 y 두 숫자의 곱을 계산하는 간단한 함수 f를 정의하자. 각각의 입력 변수에 대한 편미분(partial derivative)은 간단한 수학으로 아래와 같이 구해 진다.
: - 미분(Gradient)은 특정 지점(particular point) 부근의 아주 작은(infinitesimally small) 변화에 대한 해당 함수 값의 변화량(rate of change)이다.
: - 연산자 가 함수 에 적용 되어 미분 된 함수를 의미 하는 것이다. 위의 수식을 이해하는 가장 좋은 방법은 가 매우 작으면 함수 는 직선으로 근사(Approximated) 될 수 있고, 미분 값은 그 직선의 기울기를 뜻한다.
- 미분은 각 변수가 해당 값에서 전체 함수(Expression)의 결과 값에 영향을 미치는 민감도와 같은 개념이다.
: - gradient 는 편미분 값들의 벡터이다. 따라서 수식으로 표현하면 다음과 같다
: , 그라디언트가 기술적으로 벡터일지라도 심플한 표현을 위해 “the partial derivative on x” 이라는 정확한 표현 대신 “the gradient on x” 와 같은 표현을 종종 쓰게 될 예정이다.
Compound expressions with chain rule
- f(x,y,z)=(x+y)z 같은 다수의 복합 함수(composed functions)를 수반하는 더 복잡한 표현식을 고려해보자.
- 두 개의 표현식 q=x+y와 f=qz 으로 분해될 수 있음에 주목하자.
- chain rule은 이러한 gradient 표현식들을 함께 연결시키는 적절한 방법이 곱하는 것이라는 것을 보여준다. 예를 들면, 와 같이 표현할 수 있다.
- Upstream gradient 노드의 output에 대한 gradient(이미 계산).
- Local gradient : 해당 노드내에서만 계산되는 gradient.
- Downstream gradient : 노드의 input에 있는 변수에 대한 gradient.
Patterns in Gradient Flow

- add gate: Upstream gradient를 Downstream gradient값에 균등하게 분배합니다. 값은 Upstream gradient와 동일합니다.
- copy gate: upstream gradient합산하여 Downstream gradient에 나타냅니다.
- mul gate: Local gradient(입력값)을 거꾸로 곱해주는 효과를 갖습니다.
- max gate: gradient를 입력 중 정확히 하나 (정방향 패스 동안 가장 높은 값을 가진 입력)에 배포합니다.
Recap: Vector Derivatives

1. Input, output이 모두 scala일때는, 미분도 scala로 정의가 됩니다.
2. output은 scala, input은 vector인 경우, gradient는 input과 차원수가 같다. gradient의 n번째 component는 n번째 input이 조금 변화했을 때, 전체 output이 얼마나 변하는 지에 대한 값이다.
3. Input, output이 모두 다변수인 경우에, 미분(derivative)은 jacobian으로 표현된다. jacobian의 (n,m) component는 n번째 input이 변화할 때, m번째 output의 변화 정도를 의미합니다. 훨씬 간단하고 효율적으로 표현하고 계산된다.
Backprop with Vectors

- max gate의 backprob시 upstream gradient가 양수인 값만 1으로 표현된다.
- Jacobian 행렬이 sparse하며 off-diagonal 값이 모두 0이므로 explicit한 방법 대신 implicit multiplication을 수행한다.

Example: Matrix Multiplication
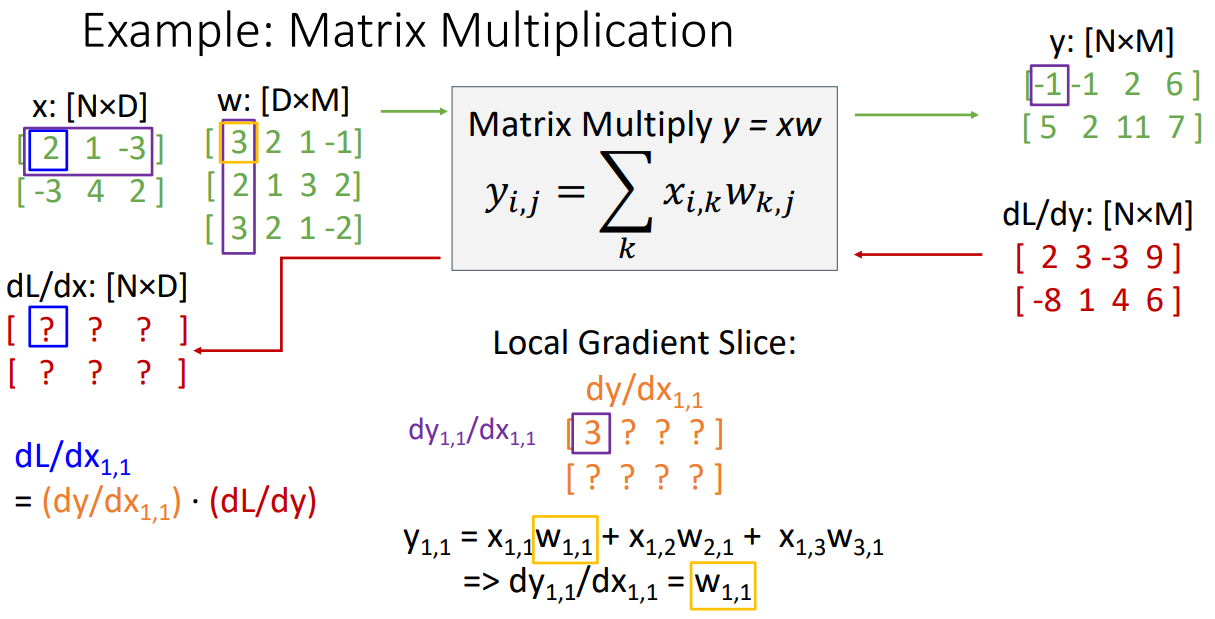
- 매트릭스 곱연산을 예제로 표현 해본다.
- 주어진 dL/dy 값(upstream gradient)을 가지고 dy/dx(Local gradient)와 dL/dx(Downstream gradient)를 구해보자
- 입력값인 을(파란색) 중심으로 시작해보자.
- Local gradient Slice(보라색)인 는 가 값에 얼마나 영향을 주는지 이다
- forward pass 계산식은 이다.
- 이를 에 대해서 derivative를 구하면 인 3이 된다.(노란색)
- 에 대하여 위 과정을 반복하면 인 2이 된다.
- 지속해보면 weight matrix w의 1번째 행이 의 첫번째 행과 동일하게 복사가 된다([3,2,1,-1] 인 형태).

- 의 두번째 행을 계산할 때는 검정색 식과 같이: 으로 표현되는데 으로 미분했을때 0이된다.
- 반복해서 계산했을 때 두번째 행은 모두 0이 된다.

- Local gradient인 으로 값(Downstream gradient)을 계산해보면 0이 된다.

- 동일한 계산 방식을 도입했을때 의 두번째 행은 weight matrix w의 3번째 행이 복사됨을 알 수 있다.
- 과정을 반복해볼때, dL/dx(Downstream gradient)의 계산 방식은 dy/dx(Local gradient)의 하나의 행과 dL/dy(upstream gradient)의 하나의 행이 inner product하여 계산 할 수 있다.

- 따라서 일반적인 형태의 수식은 위와 같다.
- 유의해야할 점은 Jacobian을 구성하여 계산하는 것이 아닌 weight matrix와 upstream gradient의 곱으로 implicit한 matrix 벡터 연산을 수행한다는 점이다. matrix의 곱연산으로 보여지지만 explicit하게 Jacobian을 구하는것이 아니다.
- x의 관점이 아닌 w를 입력으로 계산 했을때도 동일한 형태로 구성됨을 알아 낼 수 있다:
참고자료
cs231n 강의 자료
cs231n 한글 강의 자료
EECS 498-007 / 598-005 2019 강의 자료
이해를 돕기 위한 추가 자료