기본적인 수치해석법 중 하나인 뉴턴랩슨법에 대해 알아보겠습니다.
해를 구하는 방법은 크게 2가지가 있습니다.
-
Analytic Solution
-
Numerical Solution
1번은 우리가 손으로 해를 구할수 있는 방법입니다. 해를 구하시요 라는 문제와 같이 오래 걸리더라도 식으로 도출이 가능한 해를 Analytic Solution이라 합니다.
2번은 손으로 풀수 없는 비선형 방정식을 풀때 사용됩니다. 비선형문제는 Analytic Solution을 구할 수 없기(해를 도출할 수 없기) 때문에 컴퓨터를 활용한 수치해석으로 풀어야하고 뉴튼법이 이 방법들 중 하나 입니다.
뉴튼법은
f(x)=0인, x를 찾는 방법입니다.
뉴튼법의 공식은 아래와 같습니다.
xn+1=xn−f′(xn)f(xn)
이 공식을 이해하기 위해 두 가지 접근법으로 살펴 보겠습니다.
1. Linearization (선형화)
테일러 급수를 이용하여 함수를 선형화 해보면,
f(x) ≈ f(x0) + f′(x0) (x−x0)
x=xn+1
x0=xn
f(xn+1) ≈ f(xn) + f′(xn) (xn+1−xn)
이 식에서 f(xn+1)를 0으로 바꿔보면
xn+1=xn−f′(xn)f(xn)
식을 얻을 수 있습니다.
2. 기하학적 접근
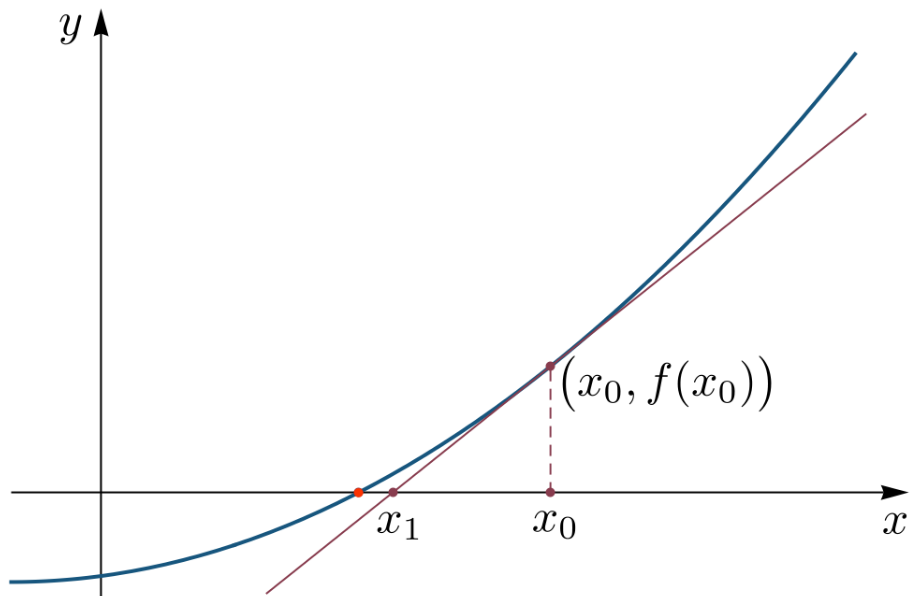
저 빨간색 선의 함수는 아래와 같습니다.
y=f′(x0)(x−x0)+f(x0)
여기서 x에 x1을 대입하면 y는 0이 되겠죠.
x1 = x0 −f′(x0)f(x0)
xn+1 = xn −f′(xn)f(xn)
이 공식을 반복 (iteration) 하다보면
xn+1−xn ⋍ 0, 0으로 수렴합니다. 여기서 우리는 n의 조건을
xn+1−xn ⋍ 0.00001 같이 넣어주면 반복을 멈추게 됩니다.
