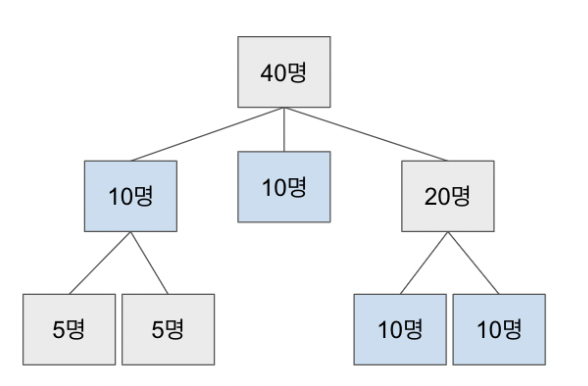
DP (Dynamic Programming)
정의: '문제의 일부분을 풀고 그 결과를 재활용하는 방법'
주어진 최적화 문제를 보다 작은 문제로 나누어 부분 문제를 풀고 해당 결과를 재활용하여 전체 문제의 해답에 이르는 방식.
어떤 문제의 입력사례의 최적해가 그 입력사례를 분할한 부분사례에 대한 최적해를 항상 포함하고 있으면, 그 문제에 대하여 최적의 원리가 성립한다.
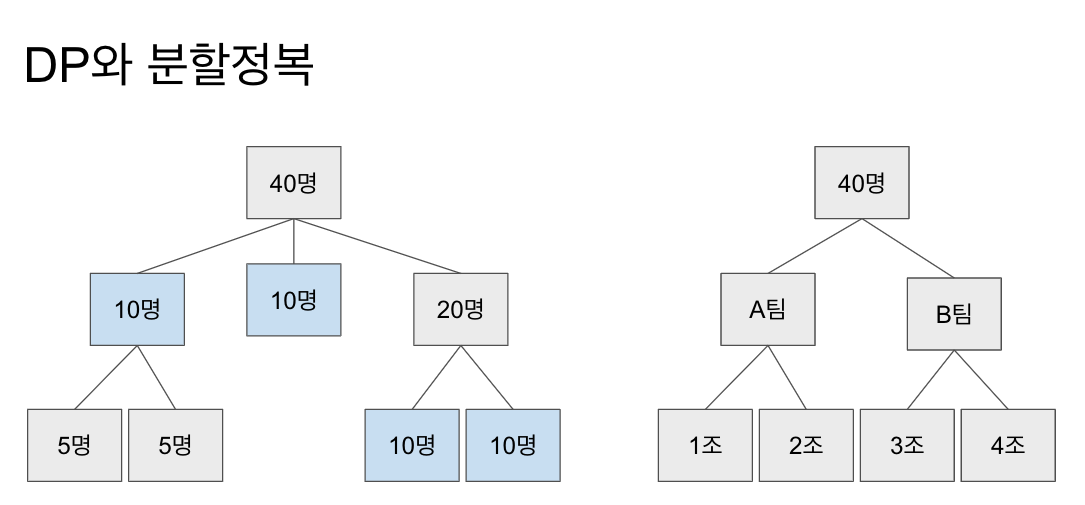
DP (왼쪽)
- 하나의 문제를 여러 서브문제로 나누어 해결한다.
- 하나의 서브문제를 해결한 방식을 저장했다가(메모이제이션을 통해) 재활용할 수 있다.
*10명짜리 문제는 같은 문제
분할정복(오른쪽)
- 하나의 문제를 여러 서브문제로 나누어 해결한다.
- 서브문제들 각각이 모두 다른 유형이다.
DP 방법론
- 메모이제이션(하향식) : 메인문제를 분할하면서 해결을 하는 법
- 태뷸레이션(상향식) : 가장 작은 문제를 먼저 해결하고 최종적으로 메인문제를 해결하는 법
예시 코드 - 피보나치 수열
# 탑다운 DP (재귀 + 메모이제이션) 피보나치 수열
# 1) 재귀를 활용하여 주어진 문제해결을 위한 함수
def dp_fib_cal(num, dp_memo):
if num < 3:
return 1
if num in dp_memo:
return dp_memo[num]
dp_memo[num] = dp_fib_cal(num - 1, dp_memo) + dp_fib_cal(num - 2, dp_memo) # 재귀
# 계산된 값들을 dp_memo[num]에 저장해놓는다.
return dp_memo[num]
# 2) 메모이제이션 개념을 위한 함수
def dp(num):
dp_memo = {} # 메모저장을 위한 변수생성
return dp_fib_cal(num, dp_memo)
print(dp(6))# 보텀업 DP (태뷸레이션) 피보나치 수열
def fib_not_recur(n):
arr = [j for j in range(n+1)] #n=6 / [0,1,2,3,4,5,6]
if n < 2:
return n
for i in range(2, n+1): # 반복 (6까지)
arr[i] = arr[i-1] + arr[i-2] #arr[2] = arr[1] + arr[0]
return arr[n] #arr[6]
print(fib_not_recur(6))
예시: Knapsack Problem
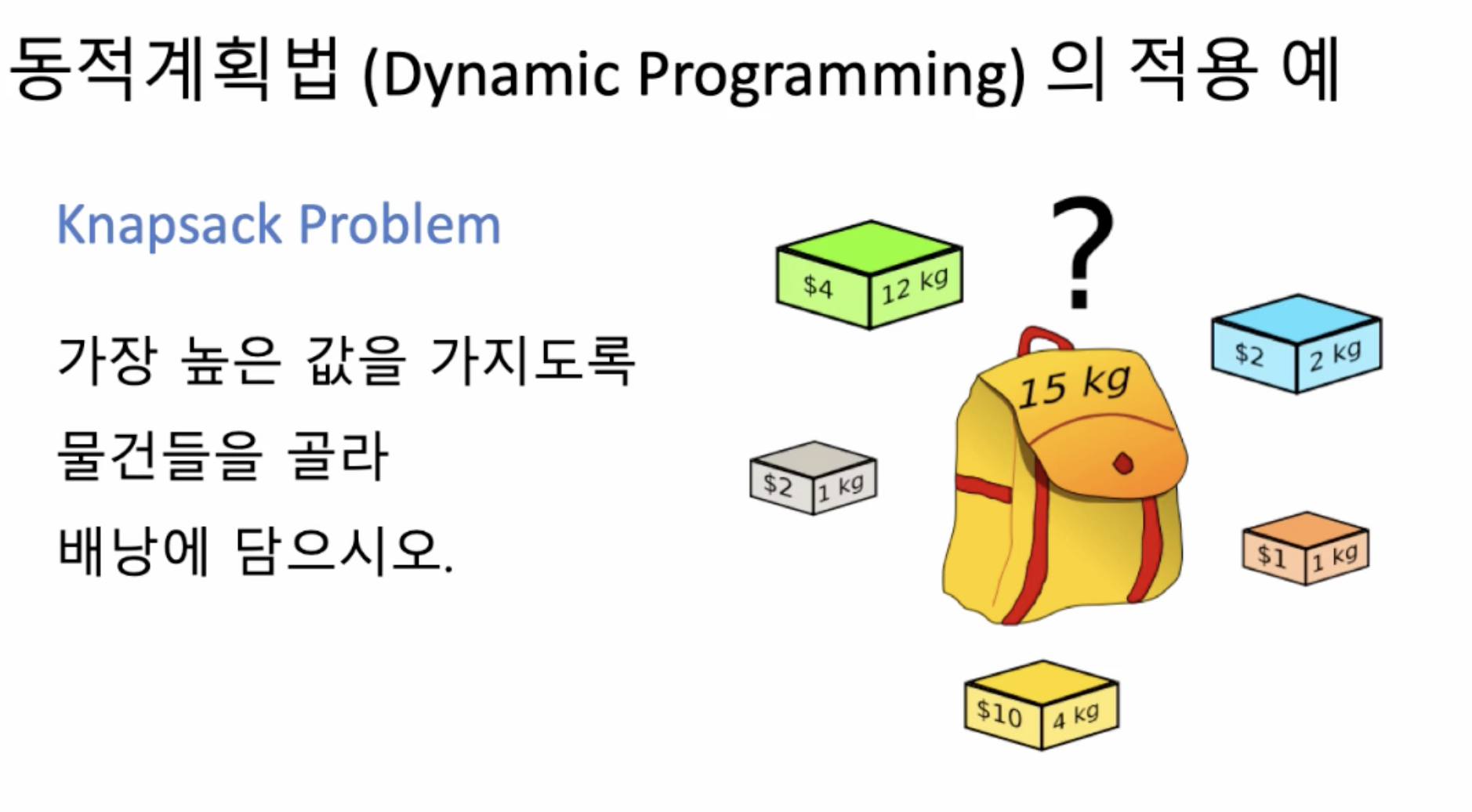
- 집합 A가 n번째 물건을 포함하고 있지 않다면,
A는 나머지 n-1개의 물건들 중에서 최적으로 고른 부분집합과 같다 - A가 n번째 물건을 포함한다면 n-1개의 물건들 중에서 최적의 부분집합 + n번째 물건을 합한 집합이다

최적해(가방에 넣은 물건들이 가장 높은 가치를 가지는 경우)를 구하려면
- i번째 물건이 배낭의 무게 한도보다 무거우면 넣을 수 없으므로 i번째 보석을 뺀 i-1개의 물건들을 가지고 구한 전 단계의 최적값을 그대로 가져온다
- 그렇지 않은 경우,
1) i번째 물건을 넣기 위해 i번째 물건만큼의 무게를 비웠을 때의 최적값에 i번째 물건의 가격을 더한 값 or
2) i-1개의 물건들을 가지고 구한 전 단계의 최적값 중 큰 것을 선택한다
레퍼런스
Dynamic Programming: 배낭 채우기 문제 (Knapsack Problem)(https://gsmesie692.tistory.com/113)
