Birthday Attack

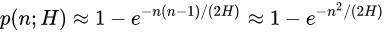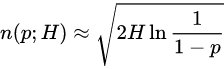
Birthday problem(생일 문제)

정의

사람이 모였을 때, 그 중 생일이 같은 두 명이 존재할 확률을 구하는 문제.
366명 이상이 모인다면 비둘기집 원리에 따라 생일이 같은 두 명이 반드시 존재한다.

확률

$p(n)=1-\frac{365!}{365^n(365-n)!}$

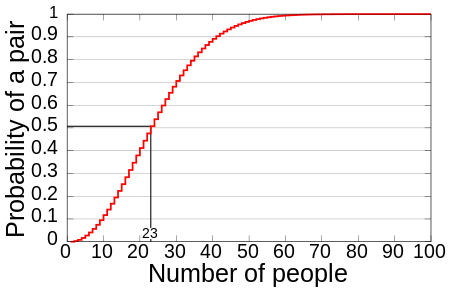
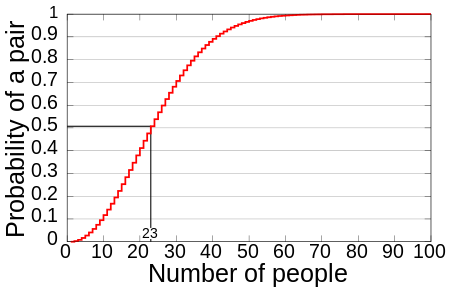
• 23명 이상만 모여도 생일이 같은 두 사람이 있을 확률이 $\frac{1}{2}$를 넘는다.
• 57명이 모이면 확률이 99%를 넘는다.

활용

이를 이용해 암호학 해시 함수(Cryptographic Hash function)의 해시 충돌(Hash Collision)을 찾을 수 있다.

Birthday Attack

정의

• 암호학적 해시 함수의 해시 충돌을 찾아내는 암호해독 공격, 확률적 결과를 기반으로 한다.
• H가지의 값을 가지는 암호학적 해시 함수 $f(x)$에 대해, $f(x1)=f(x2)$이고 $x1 \ne x2$인 두 입력값 x1, x2를 찾는 것이 해시 충돌의 목표이다.

확률

이를 찾기 위해서 n가지의 입력값을 임의로 선택한 후 해시 값을 비교한다고 할 때, 해시 충돌을 찾을 확률 $p(n;H)$은 다음과 같다.

해시 충돌을 찾기 위한 입력의 가짓수를 $n(p;H)$라 하면 다음과 같다.

$n(0.5;H)\approx1.1774\sqrt{H}$

계산 횟수의 기댓값은

$Q(H)\approx\sqrt{\frac{\pi}{2}H}$

의미

• n-bits 해시 함수의 충돌을 발견하기 위해서는 평균적으로 $\frac{\pi}{2}2^{n/2}$가지의 입력값만 조사하면 된다.
• Brute-Force 사용 시 $2^{n}$가지.

보안성 확보하기

$2^{n}$의 공격을 수행하는 공격자에 대한 보안을 확보하기 위해서는 2n-bits의 출력 길이를 가져야한다.

• 이는 Block Cipher Key 길이의 2배이다.
• Block Cipher 128-bit key는 256-bit 해시 함수와 동일한 보안 효과를 갖는다.