트리(Tree)

Ouroboros·2023년 10월 29일

heap tree 자료구조 트리 힙

자료구조

목록 보기

5/13

트리(Tree)

1) 트리(Tree)의 개념과 특징

트리는 노드로 이루어져있다.
1:N으로 이루어진 1)비선형 구조이며 계층 구조를 표현한다.
그래프의 일종이다.
- n:n ⇒ 그래프/ 1:n + 계층 ⇒ 트리
한 개의 루트 노드만이 존재하며 모든 자식 노드는 한개의 부모 노드만을 가진다.
노드가 n개라면, 간선은 n-1개이다.
어떤 노드로 가는 루트는 유일하다
- 임의의 두 노드간의 루트도 유일하다. 즉, 두 개의 정점 사이의 길이 하나이다.
트리는 이진 트리, 이진 탐색 트리, 균형 트리(AVL 트리, red-black 트리), 이진 힙(최대힙, 최소힙) 등이 있다.

2) 트리에 관한 용어

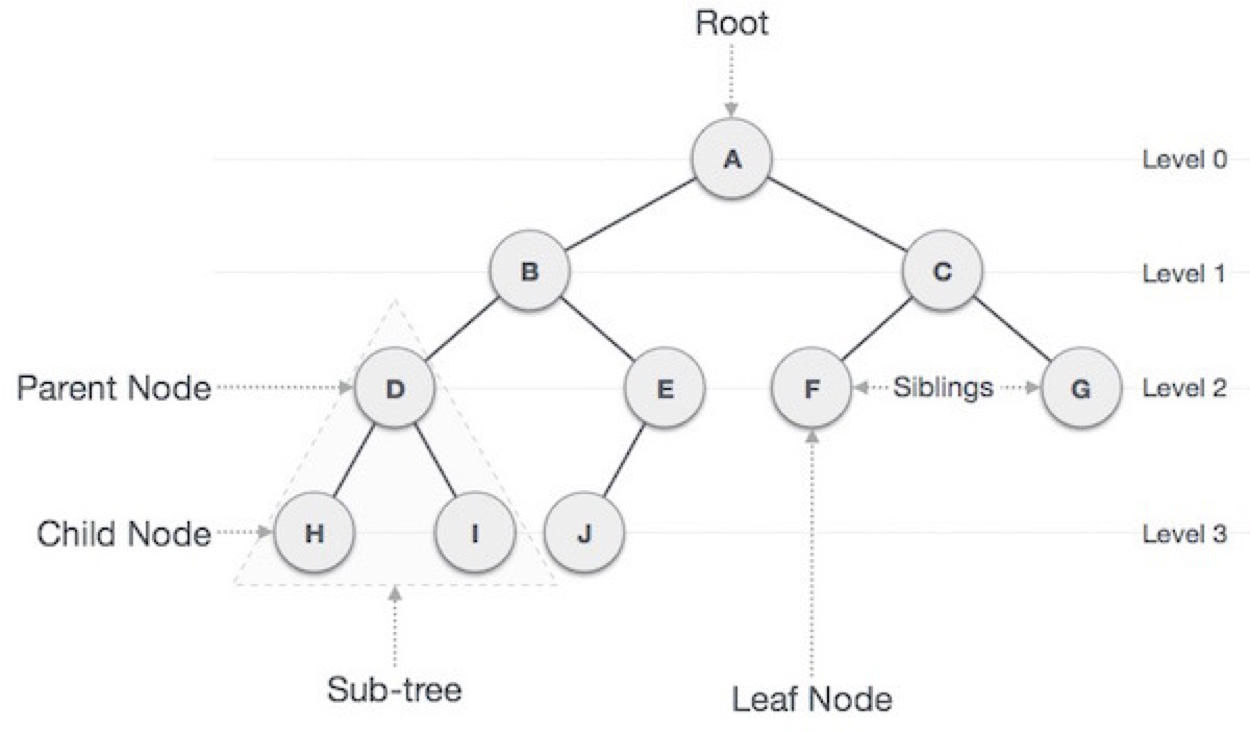
✔️ 루트 노드(root node) => A
부모가 없는 노드, 트리는 하나의 루트 노드만을 가진다.
✔️ 단말 노드(leaf node) => H, I, J, F, G
자식이 없는 노드, ‘말단 노드’ 또는 ‘잎 노드’라고도 부른다.
✔️ 간선(edge):
노드를 연결하는 선 (link, branch 라고도 부름)
✔️ 형제(sibling) => H와 I / F와 G
같은 부모를 가지는 노드
✔️ 노드의 크기(size) => ex) B의 크기 : 6
자신을 포함한 모든 자손 노드의 개수
✔️ 노드의 깊이(depth) => ex) D의 깊이 : 2
루트에서 어떤 노드에 도달하기 위해 거쳐야 하는 간선의 수
✔️ 노드의 레벨(level) => A의 레벨:0 / B,C의 레벨:1...
트리의 특정 깊이를 가지는 노드의 집합
✔️ 노드의 차수(degree) => ex) A의 차수 : 2 / E의 차수 : 1
하위 트리 개수 / 간선 수 (degree) = 각 노드가 지닌 가지의 수
✔️ 트리의 차수(degree of tree) => 최대인 A,B,C,D : 2
트리의 최대 차수
✔️ 트리의 높이(height) => 3
루트 노드에서 가장 깊숙히 있는 노드의 깊이

3) 트리의 종류

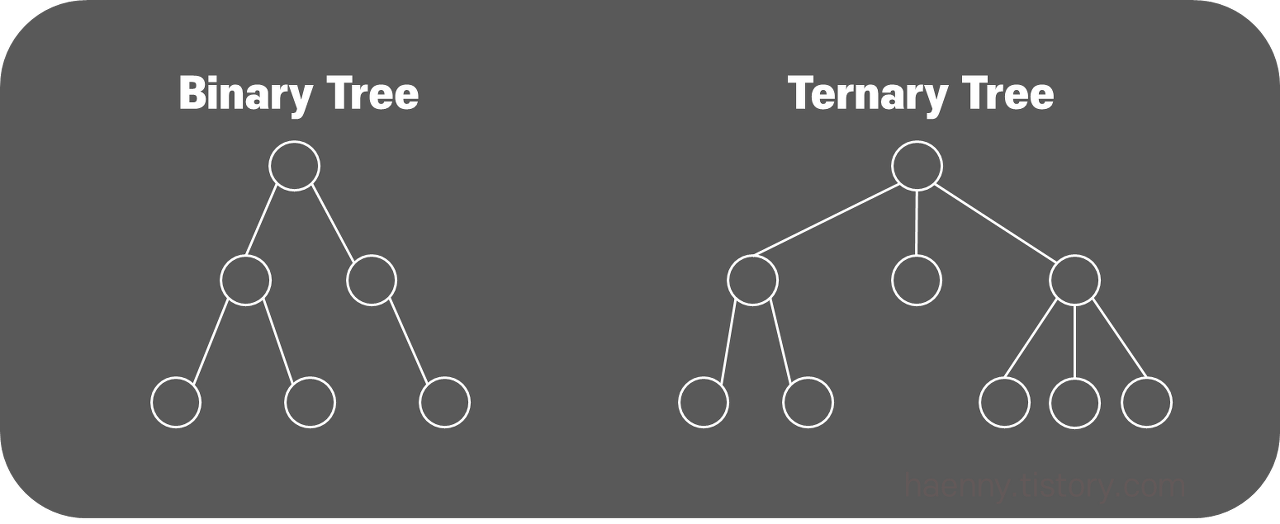
(1) 이진트리

자식노드가 최대 2개까지만 붙는 트리
자식노드가 최대 3개까지 붙는 트리는 Ternary Tree 라고 한다!

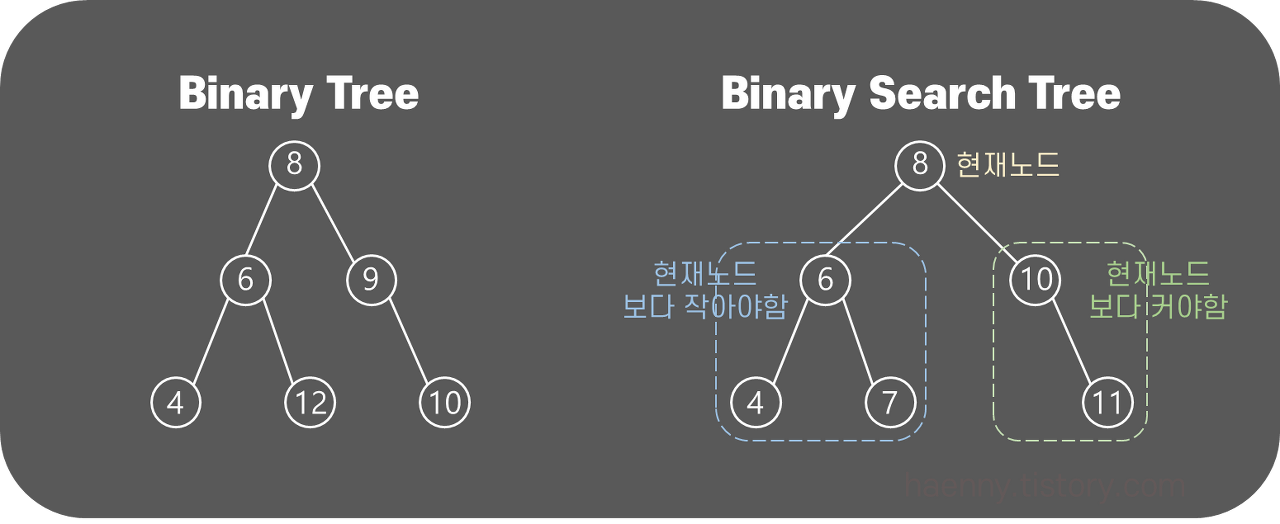
(2) 이진탐색트리

이진트리의 왼쪽 부분은 현재 노드보다 작아야하고, 오른쪽 부분은 현재 노드보다 커야한다.
따라서 현재 노드보다 큰 값을 찾으려면 오른쪽 부분을, 작은 값을 찾으려면 왼쪽 부분을 탐색하면 된다!
[이진 탐색 트리 더 알아보기]

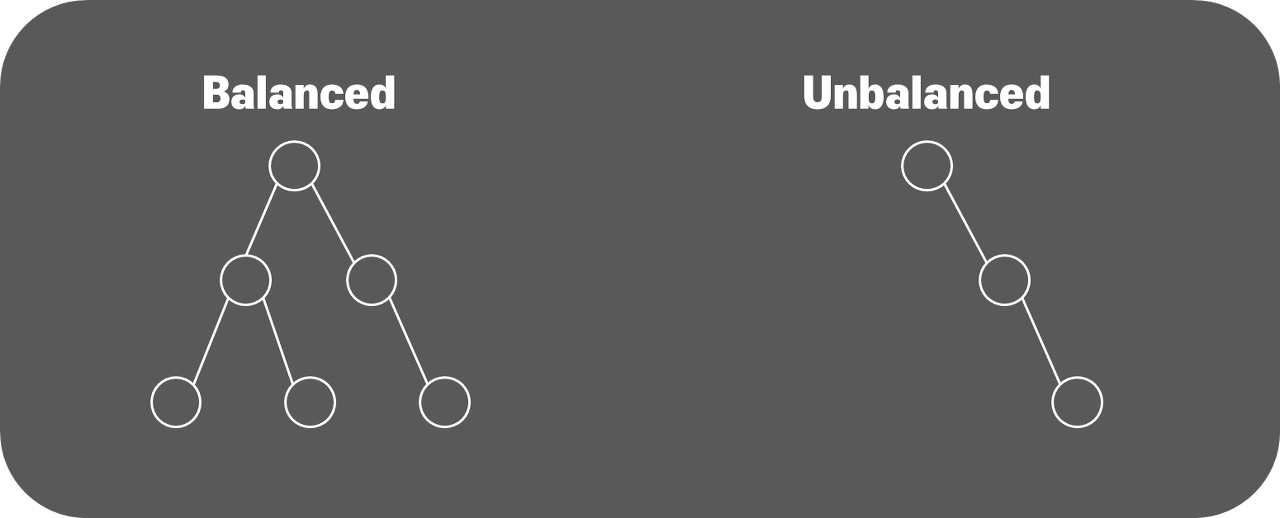
(3) 균형트리

꼭 노드의 개수가 모두 다 맞다 안맞다가 아니라 치우치지 않은 상태를 균형이 맞다라고 한다.
balance가 맞는 대표적인 트리 : 2)Red-black Tree, 3)AVL Tree

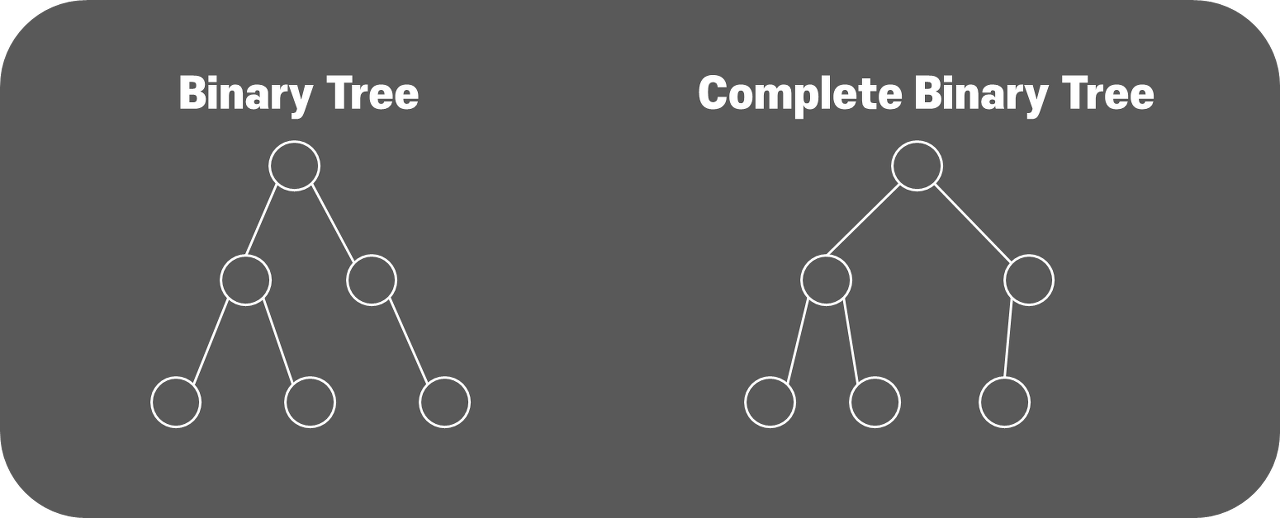
(4) 완전이진트리

마지막 레벨을 제외하고 모든 레벨이 완전히 채워져 있다.
마지막은 꼭 다 채워져 있지 않아도 되지만, 왼쪽부터 채워져 있어야 한다!

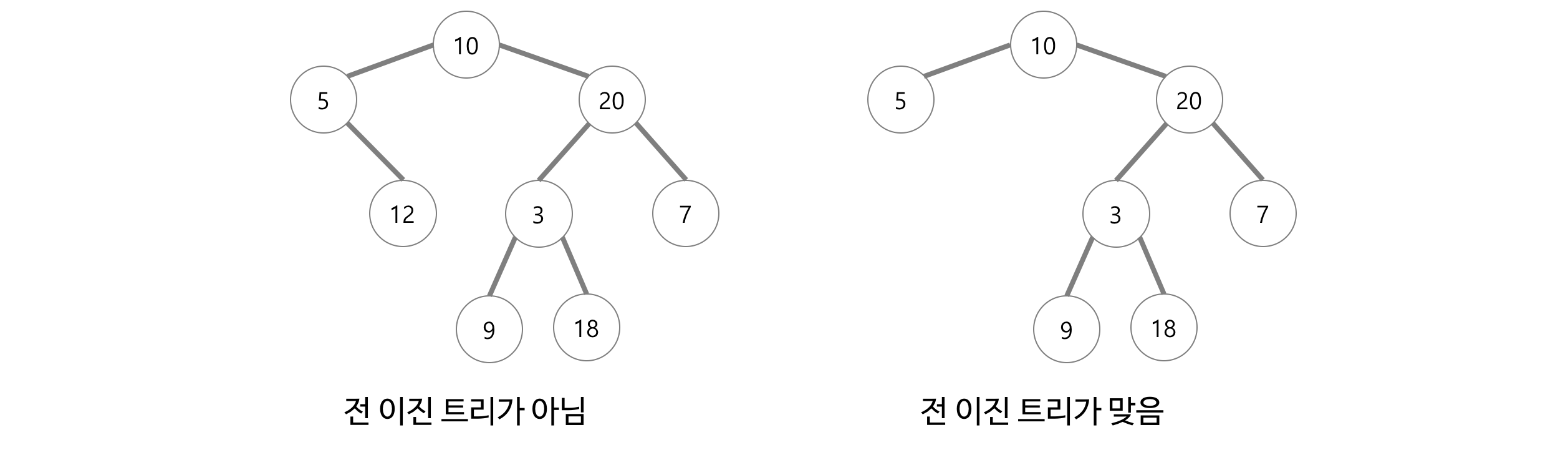
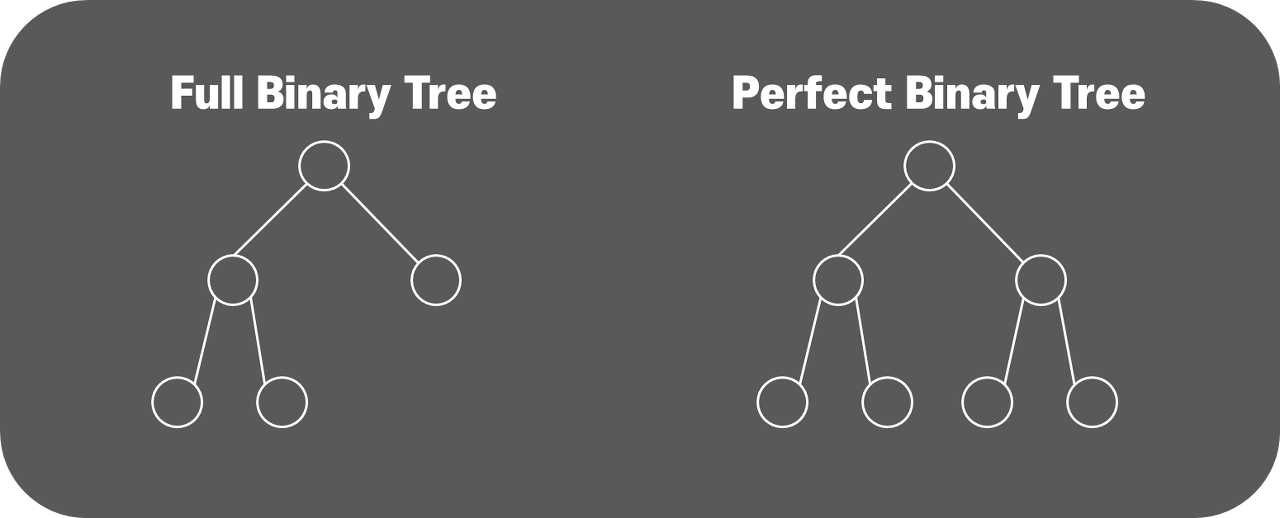
(5) 전 이진 트리(Full Binary Tree 또는 Strictly Binary Tree)

모든 노드가 0이거나 2인 트리
1이면 안된당!

(6) 완전이진트리

모든 내부 노드가 2개의 자식을 갖고 레벨도 정확하게 떨어진다.
완벽한 파라미드 구조를 형성하고 있다.
레벨이 n인 경우, 노드의 개수는 2ⁿ-1 개이다

(7) 이진힙

완전 이진 트리의 일종, 우선순위 큐를 위해 만들어진 자료구조이다.
여러 개의 갑들 중에서 최댓값이나 최솟값을 빠르게 찾아낼 수 있는 자료구조이다.

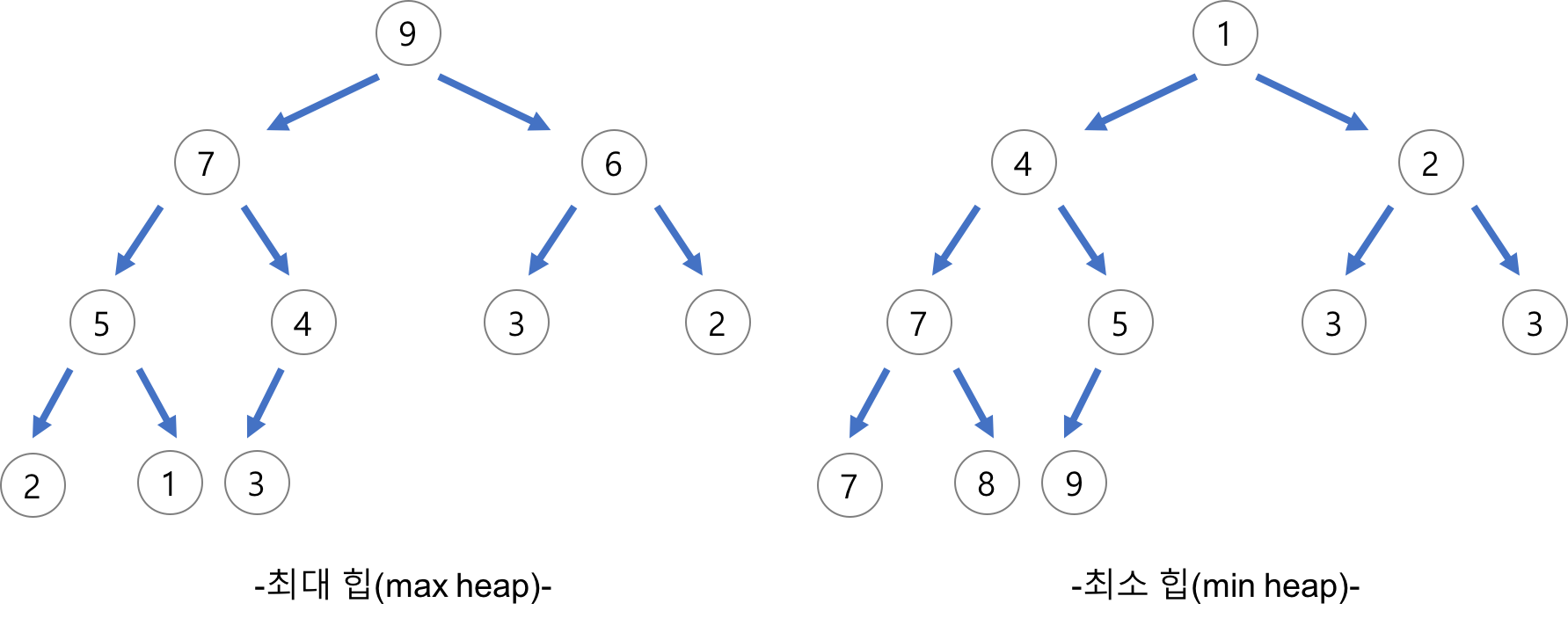
최대 힙(max heap)
부모 노드의 키값 >= 자식노드의 키값
최소 힙(min heap)
부모 노드의 키값 <= 자식노드의 키값

4) 이진트리 순회 방법

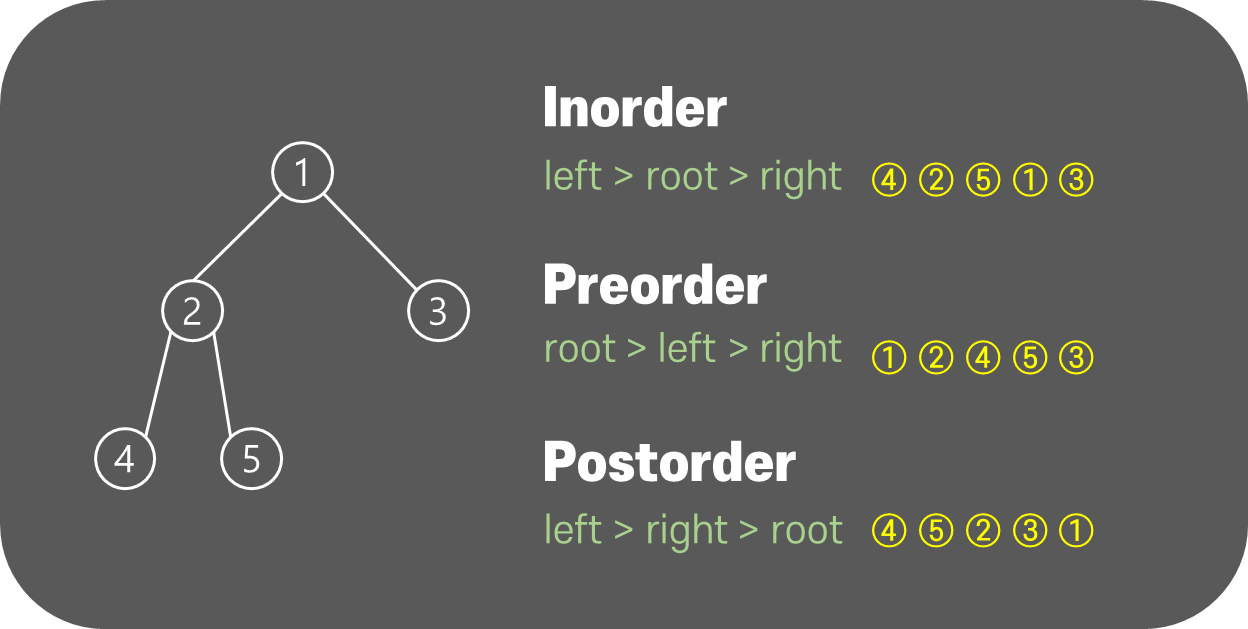
(1) 중위 순회(in-order traversal):
왼쪽 가지 -> 현재 노드 -> 오른쪽 가지

void inOrderTraversal(TreeNode node) {
  if(node != null) {
   inOrderTraversal(node.left);
   visit(node);
   inOrderTraversal(node.right);
  }
}

(2) 전위 순회(pre-order traversal):
현재 노드 -> 왼쪽 가지 -> 오른쪽 가지

void preOrderTraversal(TreeNode node) {
  if(node != null) {
   visit(node);
   preOrderTraversal(node.left);
   preOrderTraversal(node.right);
  }
}

(3) 후위 순회(post-order traversal):
왼쪽 가지 -> 오른쪽 가지 -> 현재 노드

void postOrderTraversal(TreeNode node) {
  if(node != null) {
   postOrderTraversal(node.left);
   postOrderTraversal(node.right);
   visit(node);
  }
}

주석

1) 비선형 구조:
<선형 자료구조>

하나의 자료 뒤에 하나의 자료가 존재하는 것
1:1로 이루어진 관계
배열과 리스트가 대표적이고 더 나아가서 스택, 큐도 이에 해당된다.

<비선형 자료구조>
하나의 자료 뒤에 여러개의 자료가 존재할 수 있는 것
1:N으로 이루어진 관계
트리와 그래프가 대표적이며 계층적 구조를 나타내기에 적절하다.

2) Red-black Tree:

레드 나 블랙 인 색상 속성을 가지고 있는 이진 탐색 트리이다.
루트 노드는 블랙이다.
모든 리프 노드들(NIL)(트리의 가장자리에 있는, 자식노드가 없는 노드)은 블랙이다.
레드 노드의 자식노드 양쪽은 언제나 모두 블랙이다. (즉, 레드 노드는 연달아 나타날 수 없으며, 블랙 노드만이 레드 노드의 부모 노드가 될 수 있다)
어떤 노드로부터 시작되어 그에 속한 하위 리프 노드에 도달하는 모든 경로에는 모두 같은 개수의 블랙 노드가 있다. = 2개의 블랙노드!

3) AVL Tree: