AVL 트리
AVL트리는 자가 균형 이진 탐색 트리이다.
즉 자기 스스로 균형을 잡는 이진 탐색 트리라는 뜻이다.
[이진탐색트리 추가 설명]
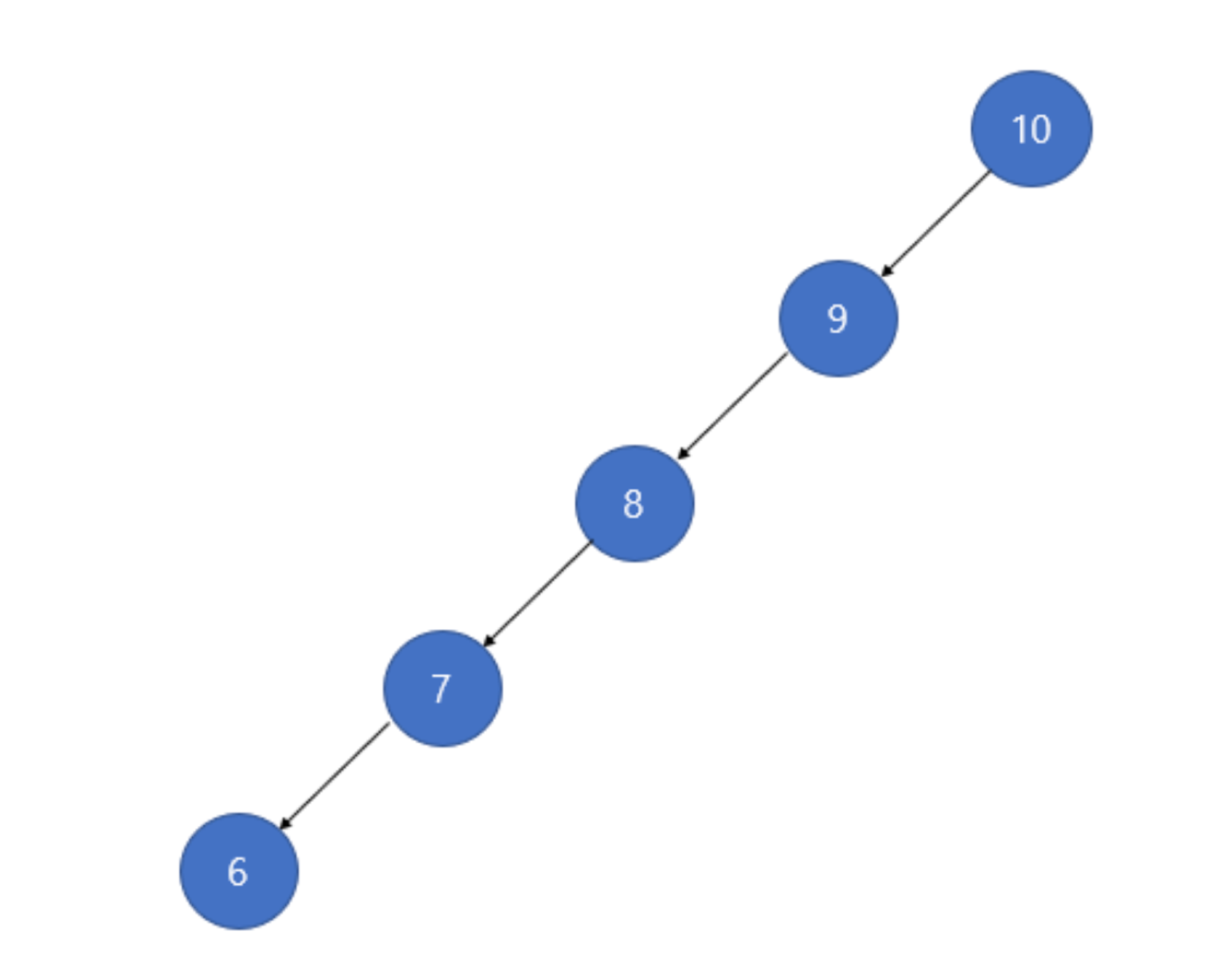
이진 탐색 트리는 문제를 발생시킬 수 있다.
위 그림과 같이 한쪽으로 노드가 쏠릴 수가 있다.
이진탐색트리의 탐색 시간은 O(logN)이지만, 이렇게 되면 (노드가 한쪽으로 편향되어 있을 경우) 탐색시간이 O(N)가 된다. 즉 6을 찾으려면 모든 노드를 검색해야 찾을 수 있다.
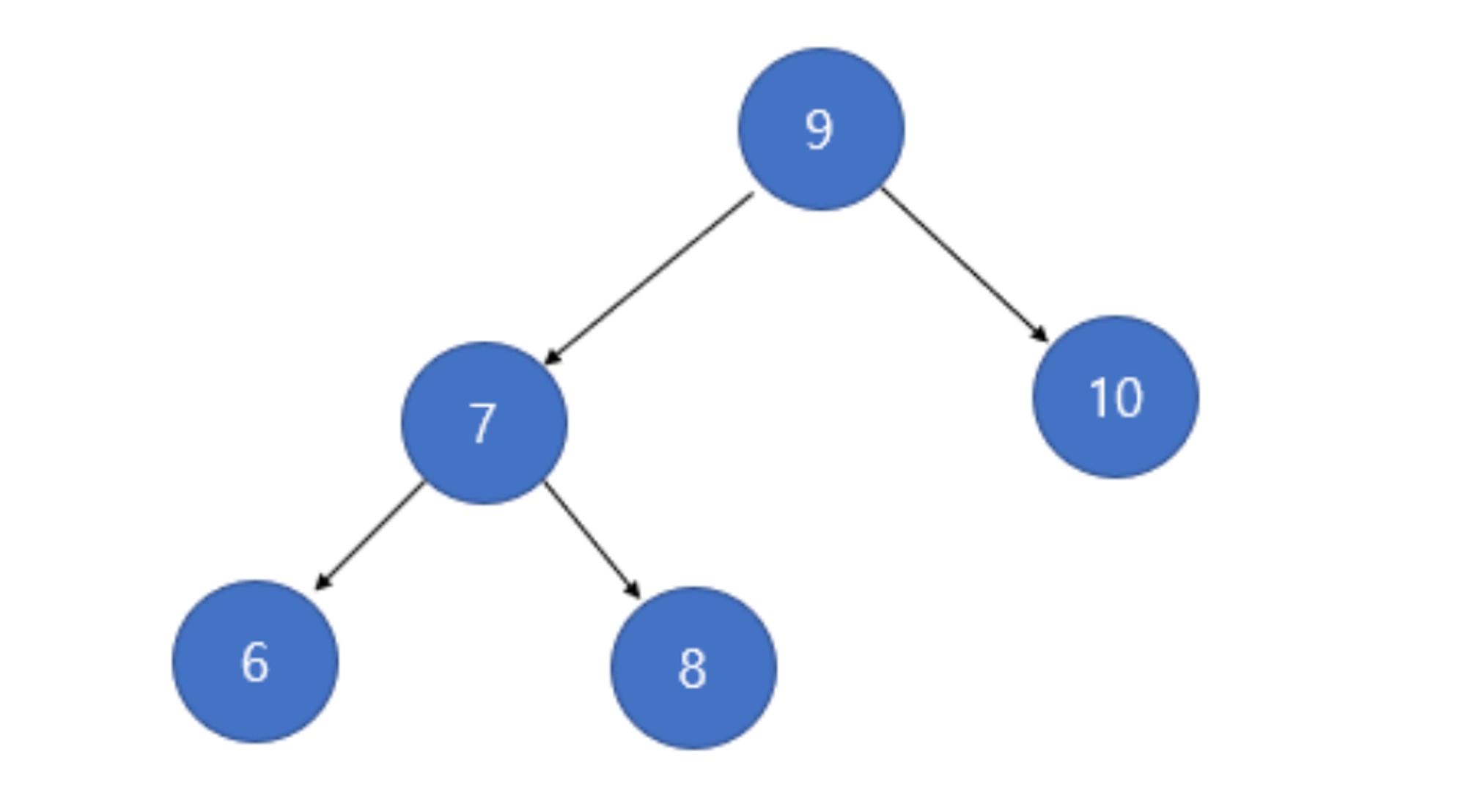
이러한 탐색 트리의 단점을 보안하기 위해서는 편향성을 보정해야 한다.
이진탐색트리의 단점을 극복할 수 있는 자료구조가 AVL트리이다. AVL트리의 특징은 다음과 같다.
- AVL 트리는 이진 탐색 트리의 속성을 가진다.
- 왼쪽, 오른쪽 서브 트리의 높이 차이가 최대 1이다.
- 어떤 시점에서 높이 차이가 1보다 커지면 회전(rotation)을 통해 균형을 잡아 높이 차이를 줄인다.
- AVL 트리는 높이를 logN으로 유지하기 때문에 삽입, 검색, 삭제의 시간 복잡도는 O(logN) 이다.
Balance Factor(BF)
AVL트리는 균형이 무너졌는지에 대해 판단할 때 Balance Factor라는 것을 활용한다. Balance Factor는 아래의 공식과 같다.
Balance Factor (k) = K의 왼쪽 서브트리의 높이 - K의 오른쪽 서브트리의 높이
- BF가 1이면 왼쪽 서브트리가 오른쪽 서브트리보다 높이가 한단계 높다는 것을 의미한다.
- BF가 0이면 왼쪽 서브트리와 오른쪽 서브트리의 높이가 같다는 것을 의미한다.
- BF가 -1이면 왼쪽 서브트리가 오른쪽 서브트리보다 높이가 한단계 낮다는 것을 의미한다.
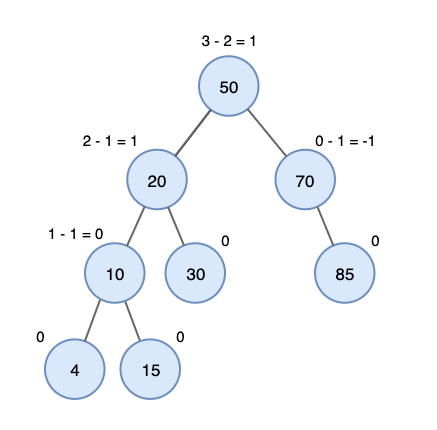
AVL트리는 모든 노드의 BF가 -1,0,1 중 하나여야 한다. 만약 이를 벗어나면 균형이 깨졌다는 것을 의미하고, 이때는 회전이 필요하다.
(사진 출처 : https://yoongrammer.tistory.com/72)
회전
AVL 트리의 회전에는 우회전과 좌회전이 있다.
<우회전>
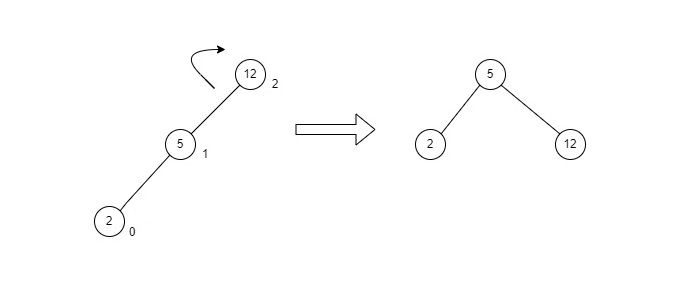
<좌회전>
삽입과 삭제를 하며 4가지 (LL, LR, RL, RR) 균형이 무너진 경우가 발생한다. 각 상황마다 방향을 달리하여 트리의 균형을 맞춘다. 각각 해결법을 알아보자.
(사진 출처 : https://www.tutorialspoint.com/data_structures_algorithms/avl_tree_algorithm.htm)
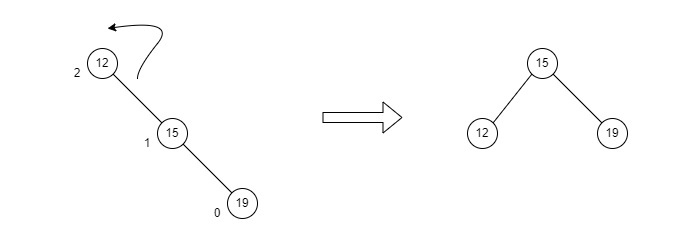
1) LL(Left Left) case

BF가 -1~1을 벗어난 노드를 기준으로 왼쪽, 왼쪽 노드가 존재한다면 LL Case이다.
이때 해당 노드를 기준으로 우회전을 적용하여,
값이 5인 노드 오른쪽 자식노드를 12노드로 변경하면 불균형이 해소된다.
2) RR(Right Right) case

BF가 -1~1을 벗어난 노드를 기준으로 오른쪽, 오른쪽 노드가 존재한다면 RR Case이다.
이때 해당 노드를 기준으로 좌회전을 적용하여,
값이 15인 노드 왼쪽 자식노드를 12노드로 변경하면 불균형이 해소된다.
3) LR(Left Right) case
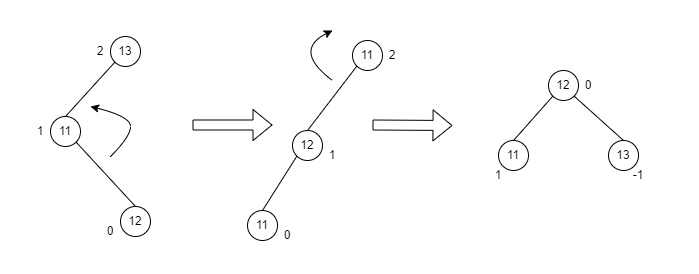
(그림 두번째 맨 위 노드 13임!)
BF가 -1~1을 벗어난 노드를 기준으로 왼쪽, 오른쪽 노드가 존재한다면 LR Case이다.
이 경우 좌회전, 우회전 순으로 총 두 번의 rotation을 수행하여 균형을 맞춘다.
- BF에 이상이 있는 노드(값이 13인노드)의 왼쪽 자식노드(값이 11인 노드)를 기준으로 좌회전을 진행한다.
-> (값이 11인 노드)는 (값이 12인 노드)의 왼쪽 자식노드가 된다.- BF에 이상이 있는 노드(값이 13인 노드)를 기준으로 우회전을 진행하여 불균형을 해소한다.
(그림 두번째 맨 위 노드 13임!)
4)RL(Right Left) case
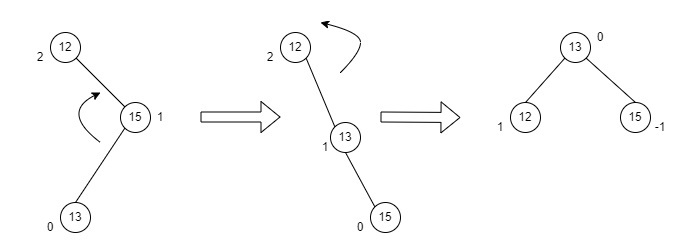
BF가 -1~1을 벗어난 노드를 기준으로 오른쪽(Right), 왼쪽(Left) 노드가 존재한다면 RL Case이다.
이 경우 우회전, 좌회전 순으로 총 두 번의 rotation을 수행하여 균형을 맞춘다.
- BF에 이상이 있는 노드(값이 12인노드)의 오른쪽 자식노드(값이 15인 노드)를 기준으로 우회전을 진행한다.
-> (값이 15인 노드)는 (값이 13인 노드)의 오른쪽 자식노드가 된다.- BF에 이상이 있는 노드(값이 12인 노드)를 기준으로 우회전을 진행하여 불균형을 해소한다.
참고자료
1) https://code-lab1.tistory.com/61
2) https://yoongrammer.tistory.com/72
3) https://80000coding.oopy.io/bb1f6ce7-2377-4d58-8e5f-f491458cc118
