이진탐색트리란?
▶️ 이진탐색트리는 1)이진트리와 연결리스트를 결합한 구조이다.
->이진트리의 탐색 능력과 연결리스트의 입력, 삭제 능력이 가능하게끔 고안되었다.
- 이진트리의 경우 탐색은 O(logn)으로 빠르지만 입력, 삭제가 불가능하다.
연결리스트의 경우 입력, 삭제를 할 경우 O(1)로 효율적이고 빠르나 탐색의 경우 O(N)의 시간 복잡성이 발생한다.
▶️ 노드의 속성
- 각 노드에 값이 있다.
- 노드들의 왼쪽 서브쿼리에는 해당 노드보다 작은 값을 지닌 노드들이 있다.
- 노드들의 오른쪽 서브쿼리에는 해당 노드보다 큰 값을 지닌 노드들이 있다.
- 좌우하위노드들은 각각이 다시 이진 탐색 트리여야 한다.
▶️ 이진 탐색 트리는 중회 순회 방식이다.
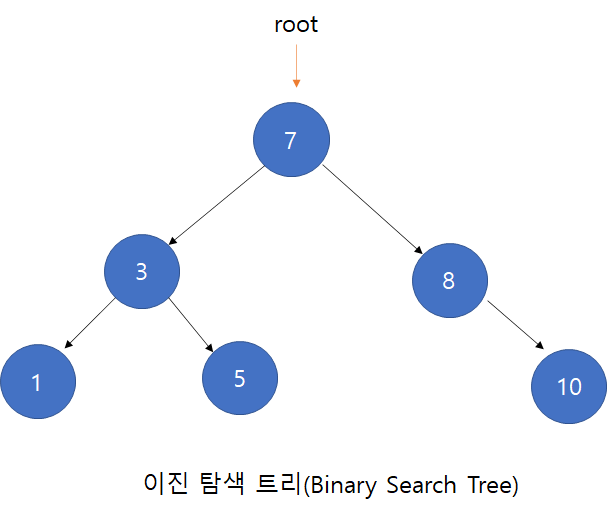
- 왼쪽 서브트리-노드-오른쪽 서브트리 순으로 순회
- 1->3->5->7->8->10
이진 탐색 트리에서의 검색(retreive, search)
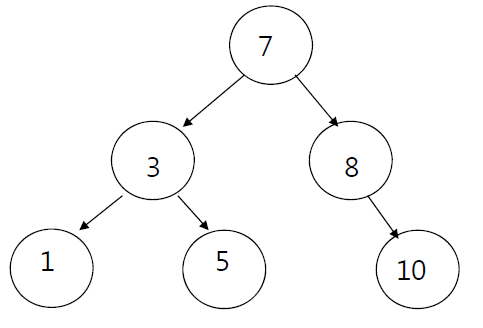
<값을 찾는 경우>
이진탐색트리에서 1을 검색(retreive, search)한다고 가정해 보자!
먼저 루트노드 <7>과 1을 비교한다. 비교했을 때 1은 7보다 작은 값이므로 왼쪽 서브트리에서 찾게 된다. 오른 쪽 서브트리(8,10)은 고려할 필요가 없다.
그 다음 왼쪽 서브트리의 루트 노드인 <3>과 1을 비교한다. 비교했을 때 3보다 작으므로 왼쪽 서브트리에서 찾게 된다. 그 다음 루트노드인 <1>과 1을 비교한다. 찾았다!
1을 검색할 때 비교하는 값
7,3,1
<값을 못찾는 경우>
이진탐색트리에서 9을 검색한다면?
위의 방법대로 10까지 찾는데도 원하는 값(9)를 찾지 못했다. 10은 트리의 잎새노드(leaf node)이기 때문에 서브트리가 존재하지 않는다. 따라서 10까지 탐색한 후 '값을 찾지 못했다'고 반환하고 검색을 종료한다.
9을 검색할 때 비교하는 값
7,8,10
▶️ 이진탐색트리에서 검색할 때 계산복잡성은 2)트리의 높이가 h일 때 O(h)가 된다. 최악의 경우 잎새노드까지 탐색한다.
즉, 이 때 h번 비교 연산을 수행한다.
이진 탐색 트리에서의 삽입(insert)

삽입을 하기 전, 검색을 수행한다.
트리를 검색한 후 키와 일치하는 노드가 없으면 마지막 노드에서 키와 노드의 크기를 비교하여서 왼쪽이나 오른쪽에 새로운 노드를 삽입한다.
만약 위 트리에서 100을 추가하려고 한다면 제일 오른쪽 잎새노드의 오른쪽 자식노드를 만들고 여기에 붙이면 된다.
이진탐색트리의 삽입 연산에 소요되는 계산복잡성은 트리의 높이가 h일 때 O(h)가 된다. 삽입할 위치의 잎새노드까지 찾아 내려가는 데 h번 비교를 해야 한다.
이진 탐색 트리에서의 삭제(delete)
<자식노드가 없는 경우>
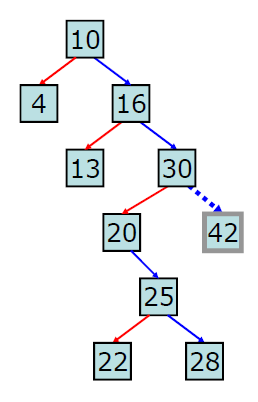
해당 노드(42)를 그냥 없애기만 하면 된다.
<자식노드가 하나 있는 경우>
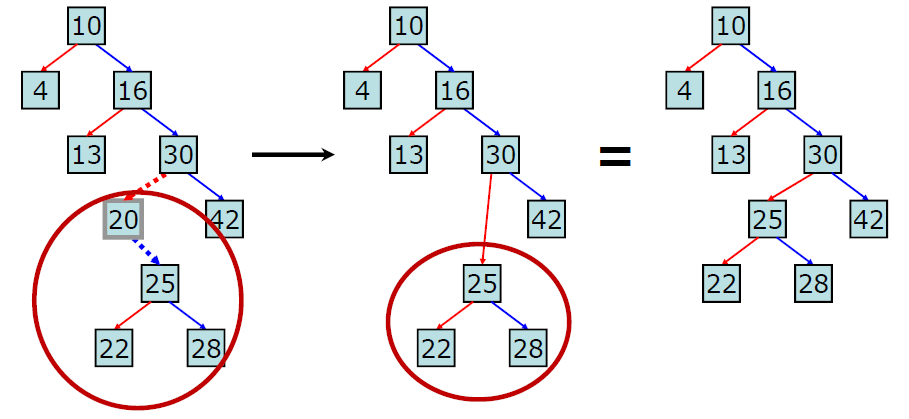
20은 자식노드가 하나이다. 20인 루트노드로 하는 서브트리(25,22,28)의 모든 값은 20의 부모노드인 30보다 작거나 같다.이진탐색트리의 속성 때문이다.(30의 왼쪽 노드트리에 20이 있기 때문에) 따라서 20을 지우고, 20의 하나뿐인 자식노드(25)와 20의 부모노드(30)를 연결해도 이진탐색트리의 속성이 깨지지 않는다!
<자식노드가 하나 이상 경우>
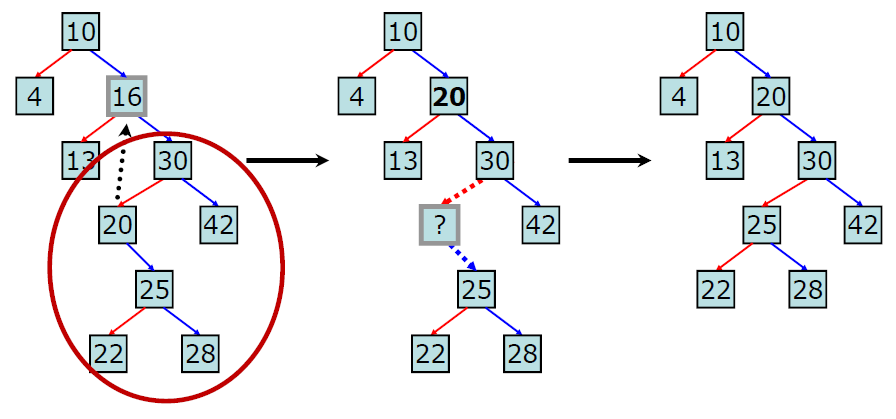
순회 경로 : 4 -> 10 -> 13 -> 16 -> 20 -> 22 -> 25 -> 28 -> 30 -> 42
predecessor : 삭제 대상 노드의 왼쪽 서브트리 가운데 최대값(13)
successor : 삭제 대상 노드의 오른쪽 서브트리 가운데 최소값(20)
16을 삭제하려고 할 때, 16 위치에 20을 복사해 둔 후, 기존 20 위치에 있던 노드를 삭제하게 되면 이진탐색트리 속성을 만족할 수 있고 원하는 결과를 얻을 수 있게 된다. 물론 16 위치에 predecessor인 13을 놓고, 기존 13 위치에 있던 노드를 삭제해도 원하는 결과를 얻을 수 있다.
부가설명
1)이진트리 : 각각의 노드가 최대 두 개의 자식 노드를 가지는 트리 자료구조
[트리와 이진트리 설명 바로가기]
2)트리의 높이 :
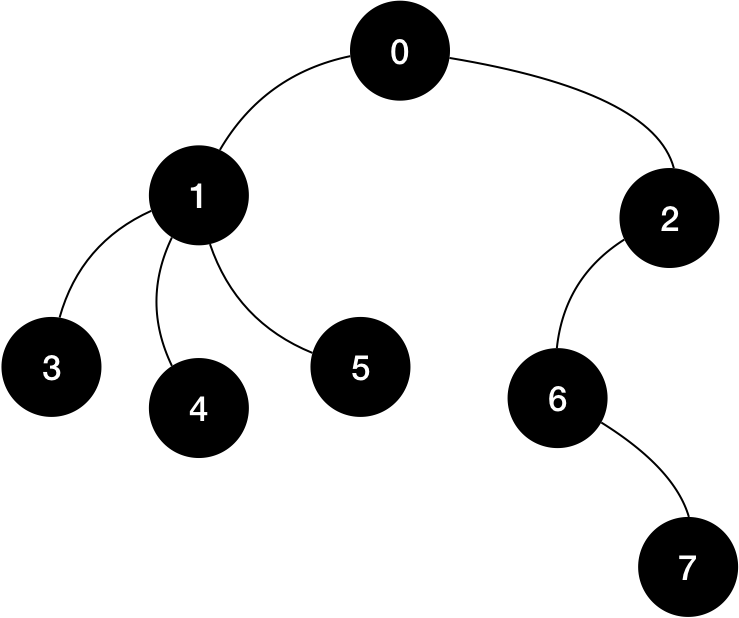
트리의 높이는 루트로부터 가장 멀리 떨어진 노드와의 거리로 정의된다. 예를 들어, 아래의 트리에서 0번 노드가 루트라고 하면, 7번 노드까지의 거리가 가장 멀고, 그 거리는 3이다. 따라서 이 트리의 높이는 3이 된다.
참고자료
1)https://ratsgo.github.io/data%20structure&algorithm/2017/10/22/bst/
