다시 알아보자 zip
어제 IntArray와 BooleanArray를 zip으로 묶으려고 할 때 List 형만 가능해서 불가능하다고 이해했었다.

그런데 말입니다… 이 말은 일부만 맞는 말이었다! Int 배열과 Boolean 배열은 zip 사용이 불가하지만, 자료형이 정해지지 않은 그냥 배열(Array)끼리는 사용이 가능하다. 또한 같은 자료형의 배열끼리도 사용이 가능하다. 따라서 다음과 같은 코드가 가능하다.
var a = arrayOf(1, 2, 3)
var b = arrayOf("a", "b", "c")
a.zip(b).map { (a, b) -> "$a$b" } // ["1a", "2b", "3c"]
(a zip b).map { (a, b) -> "$a$b" } // ["1a", "2b", "3c"]어제 내가 만약 코틀린 문서까지 들여다보고 공부했다면 오늘 이렇게 다시 공부하는 일은 없었을텐데 원통스러울 따름이다.
범위가 작을 때도 효율을 따져야 하나?
이번에 풀었던 문제는 주어지는 두 정수 사이 정수들의 약수의 개수를 구한 뒤, 그 개수가 짝수면 해당 수를 더하고 아니면 뺄셈을 하는 문제였다.
일반적으로 정수 n의 약수를 구하려면 n을 1부터 n까지의 수들로 나눴을 때, 나머지가 0인 수를 찾으면 된다. 그런데 n이 1억이 넘어가는 수라면.. 1경이 넘어간다면.. 게다가 약수를 구하려는 수가 여러 개라면.. 상당히 시간이 오래 걸릴 것이다. 물론 아직 코틀린의 ㅋ자도 모르는 내가 할 소리는 아니긴 하지만 하우에버, 이런저런 고민도 해가면서 알아가는 거겠지란 마음이다.
사실 나는 극한의 짧은 코드충이라 효율 따위 개나줘버려 라는 식으로 문제를 풀곤 한다. 좋은 방법이 아닌 것 같지만 그래도.. 짧으면 기분이 좋크든요.. 아무튼 이렇게 효율을 따지지 않는 내가, 배열을 여러 번 순회해야 되는 경우는 좀 조심스럽게 풀이하는 편이다. 그냥 길게 푼다는 것임
n의 약수는 약수끼리 곱하면 n이 나온다. 즉, 절반만 구하면 된다. 더 나아가면 n의 제곱근까지만 탐색하면 된다. 구한 약수들로 n을 나누면 나머지 약수들이 나오게 되니까 말이다. 그래서 처음에는 이걸 이용해 풀었었다. 당연히 문제의 제한 사항은 눈에 담지도 않고 코드를 싸질렀다!
class Solution {
fun yaksu(n: Int): Int {
// n의 제곱근까지만 탐색
var end = Math.sqrt(n + 0.0)
var half = (1..end.toInt()).filter { n % it == 0 }.size
// 겹치는 경우 대응 ex. 16의 제곱근 4가 중복
return if (end%1 == 0.0) half*2 - 1 else half*2
}
fun solution(left: Int, right: Int): Int {
return (left..right).fold(0) { total, n -> total + if (yaksu(n) % 2 == 0) n else -n }
}
}위에서 나왔듯이 문제에는 "제한 사항"이라는 것이 주어진다. 풀고 나서 확인해보니 숫자 n은 최대 1,000 밖에 안됐었고.. 내 머리로는 안되겠지만 컴퓨터한테 몇천 번, 많아봤자 몇만 번의 연산은 누워서 떡 먹기 수준일 것이다. 그래서 제곱근이고 뭐고 냅다 그냥 1부터 n까지 탐색해도 되었던 것이다.
fun yaksu(n: Int): Int {
return (1..n).filter { n % it == 0 }.size
}
fun solution(left: Int, right: Int): Int {
return (left..right).fold(0) { total, n -> total + if(yaksu(n) % 2 == 0) n else -n }
// 사실 한 줄로도 가능...
return (left..right).fold(0) { total, n -> total + if((1..n).filter { n%it == 0 }.size % 2 == 0) n else -n }
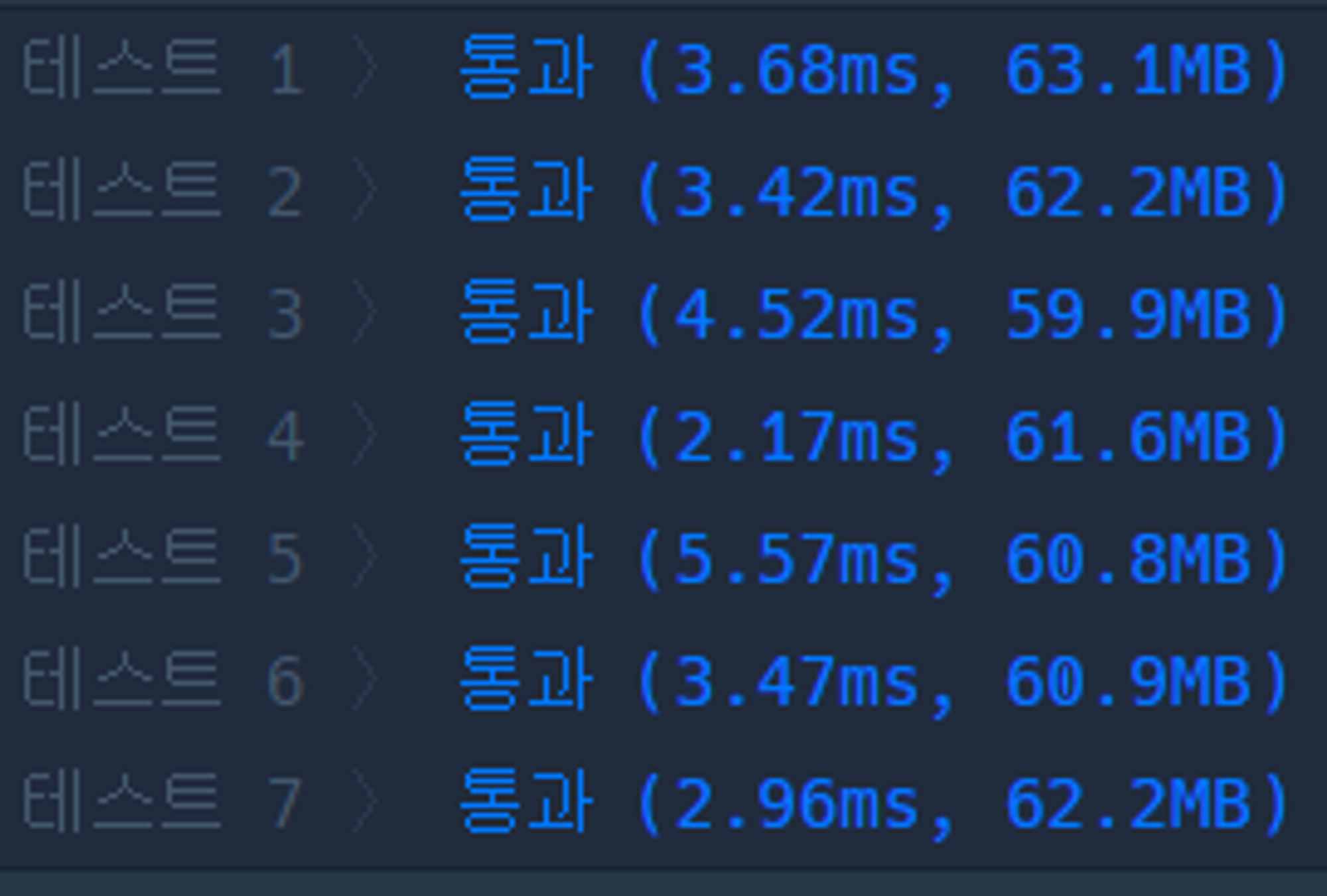
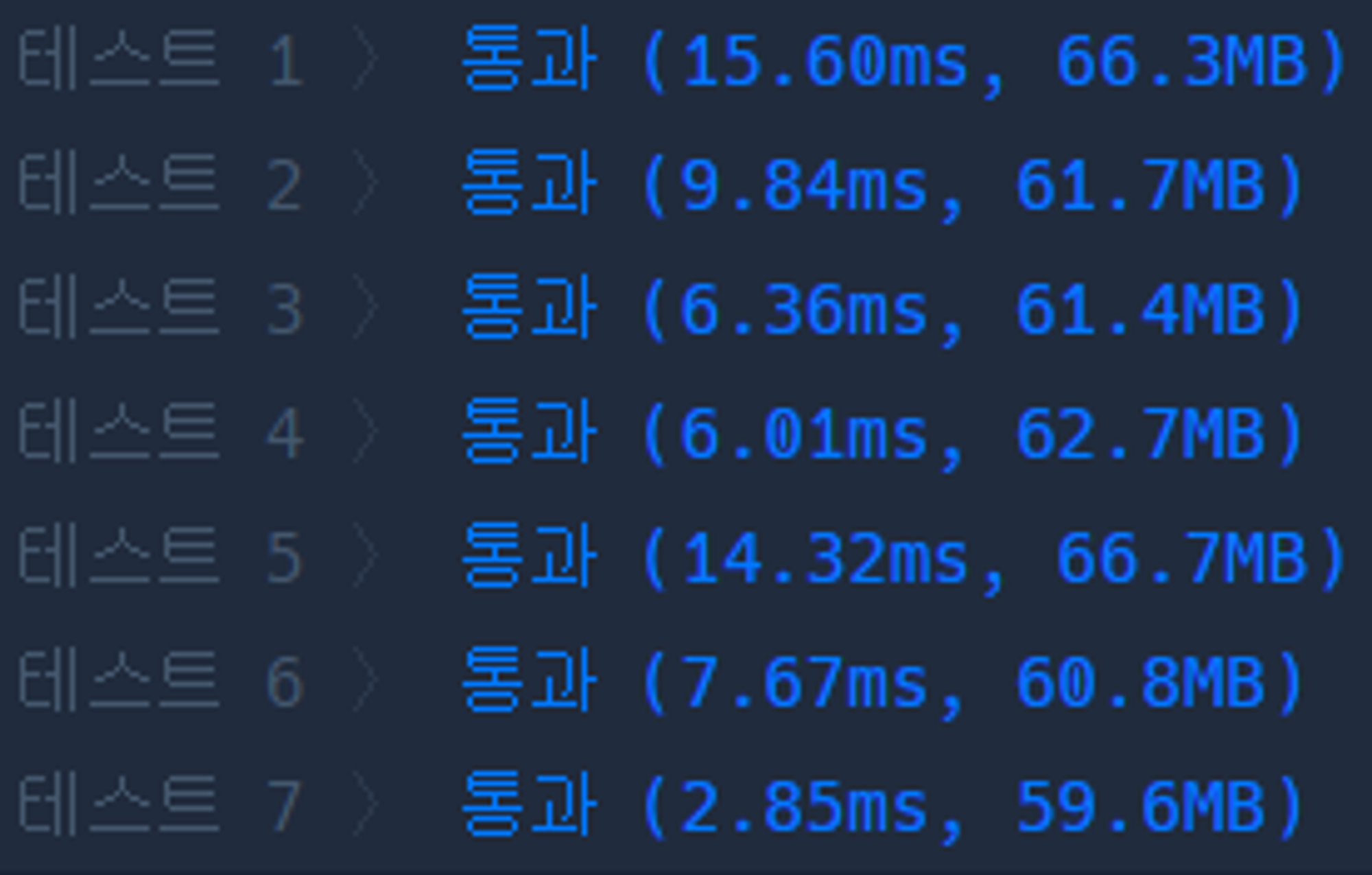
}그래도 기왕 여러 번 풀이한 거 소요 시간을 비교해봤다.
| 제곱근까지 탐색했을 때 | n까지 탐색했을 때 | 함수 분리 없이 작성 |
|---|---|---|
 |
 |
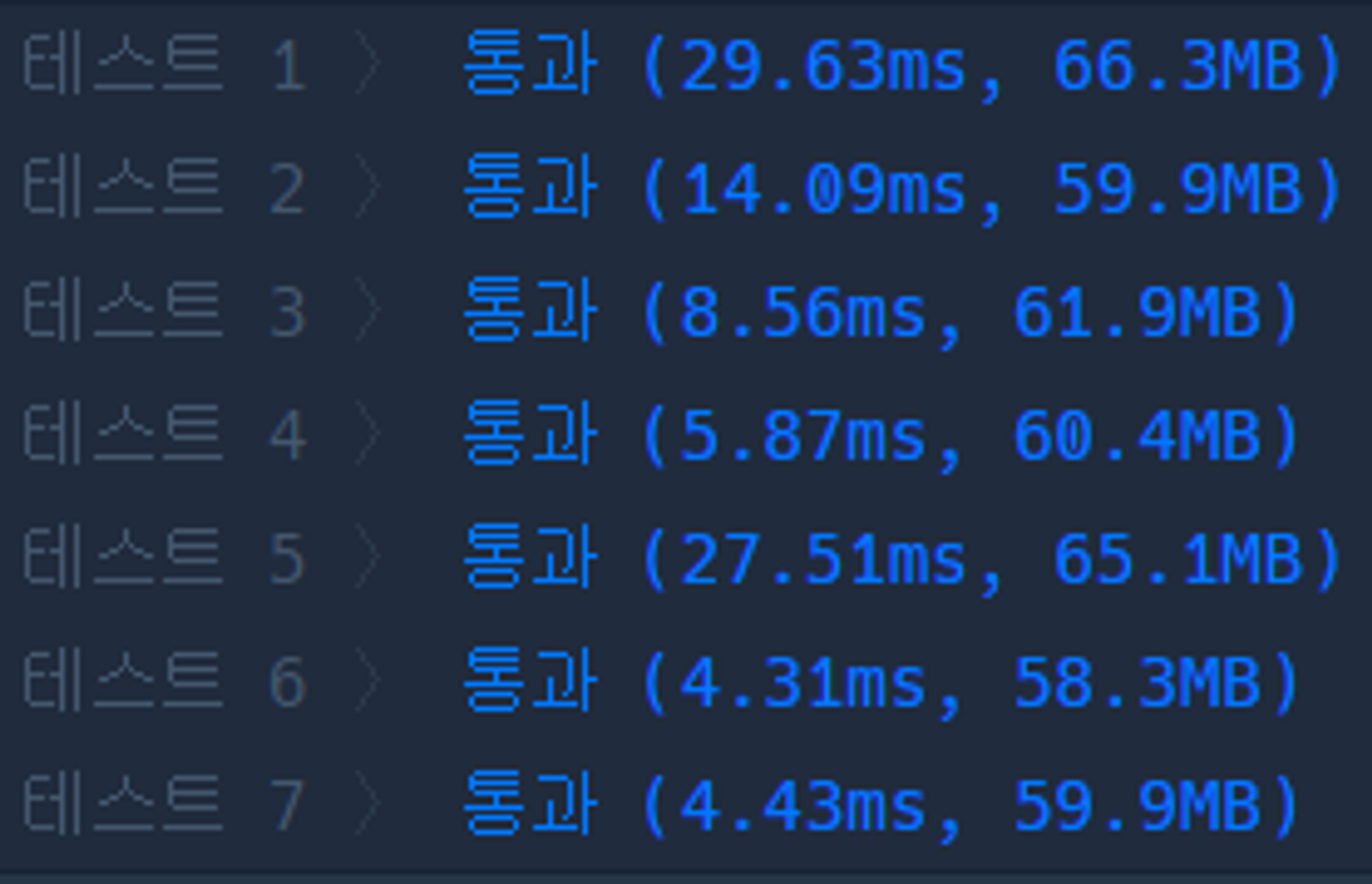 |
제곱근까지 탐색했을 때가 조금 더 빠른 것 같긴 하지만 이번 문제에서는 굳이 생각할 요소가 아니었던 것 같다. 앞으로는 제한 사항도 잘 챙겨보도록 하자. 😭

