숭실대학교 컴퓨터학부 최지웅 교수님의 강의를 수강하며 학습한 내용입니다.

---

Chained Matrix Multiplication Algorithm

(연쇄행렬곱셈 알고리즘)

Definition

: 연쇄적으로 행렬을 곱셈하는데에 있어서 행렬곱셈의 순서에 따라 달라지는 기본적인 곱셈연산 횟수의 최적의 곱셈양식을 구하는 알고리즘 입니다.

i j Matrix와 j k Matrix를 곱셈하기 위해 일반적으로 i j k 만큼의 곱셈이 필요합니다.

하단에 주어진 문제상황을 참고하도록 하겠습니다.

Problem

문제상황 : n개의 행렬을 곱하는데 필요한 기본적인 곱셈의 횟수의 최소치를결정하고, 그 최소치를 구하는 순서를 결정하라.

• 입력
  : 행렬의 수 n와 배열 d[0..n], d[i-1] * d[i]는 i번째 행렬의 규모를 나타낸다.
  ex) A1 ~ A3 를 곱셈하는 경우 : A1 ( a1 x b1 ), A2 ( a2 x b2), A3 ( a3 x b3)

  (d[0], d[1]) 에는 (a1, b1), (d[1], d[2])에는 (a2, b2), (d[2], d[3])에는 (a3, b3) 초기화

• 출력
  : 기본적인 곱셈의 횟수의 최소치를 나타내는 minmult;
  최적의 순서를 얻을 수 있는 배열 P, 여기서 P[i][j]는 행렬 i부터 j까지가 최적의 순서로 갈라지는 기점

Pseudo Code

int minmult(int n, const int d[], index P[][])
{
	index i, j, k, diagonal;
	int M[1..n, 1..n];
	for(i=1; i <= n; i++)
		M[i][i] = 0;
	for(diagonal = 1; diagonal <= n-1; diagonal++)
    	for(i=1; i <= n-diagonal; i++)
    	{
			j = i + diagonal;
			M[i][j] = minimum(M[i][k]+M[k+1][j]+d[i-1]*d[k]*d[j]);i <= k <= j-1
			P[i][j] = 최소치를 주는 k의 값
		}
	return M[1][n];
}
//강의 교안에서 참조한 pseudo code 입니다. 

Chained Matrix Multiplication Algorithm은 Dynamic Programming에 의거합니다.

why?
A1 x A2 x A3 곱셈횟수의 최적을 구하는 경우

case 1) ((A1 x A2) x A3)
A1 x A2도 최적, A3도 최적의 경우의 곱셈이여야 전체의 경우도 최적
case 2) (A1 x (A2 x A3))
A1도 최적, A2 x A3도 최적의 경우의 곱셈이여야 전체의 경우도 최적

Code Review

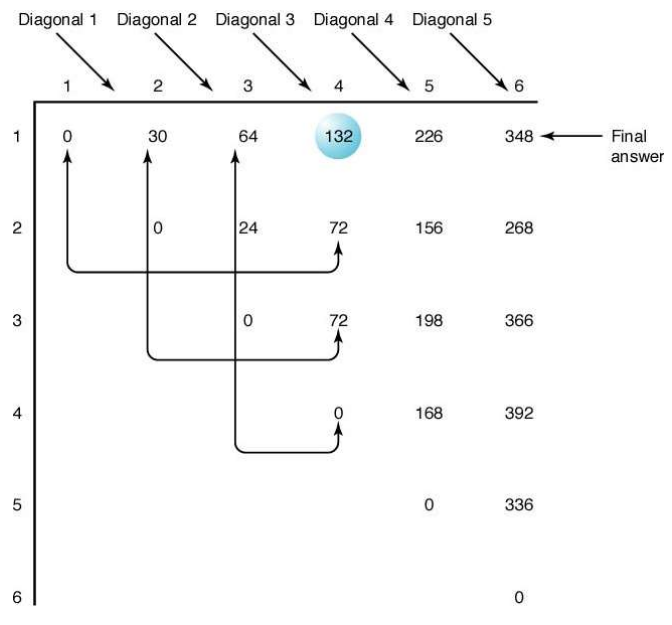
M배열의 x행 y열에는 x번째 행렬부터 y번째 행렬까지 곱셈의 최적의 경우 곱셈횟수가 각각 저장되어 있습니다. 각각의 경우가 최적이여야 전체도 최적이 되는 특징에 따라, 해당 M배열은 M[1][4]를 구하기 위해 다음과 같은 참조 양상을 보이게 됩니다.
ex)

//강의 교안에서 참조한 자료입니다.

예시를 들어 코드설명을 보충하겠습니다.

M[1][4], 즉 A1 x A2 x A3 x A4 의 최적값을 구해보자.
결론적으로 행렬의 곱셈이므로 마지막 곱셈의 형태는 다음 중 하나일 것이다.
1. A1 x (A2 x A3 x A4)
2. (A1 x A2 x A3) x A4
3. (A1 x A2) x (A3 x A4)

세가지 경우가 도출되게 되는데 첫번째 경우가 최적이라면 A2 x A3 x A4도 최적의 상태이여야 하고, 그 경우를 고려하기 위해 M[2][3]도 최적의 경우의 값이 사전에 초기화 되어있고 이를 가져다 쓰는 형태로 알고리즘이 이루어져야 한다. (Dynamic Programming)

그래서 2중 for문을 돌며 최종적으로 A1~An까지의 최적의 경우를 구하기 위해 대각선 모양으로 배열을 차근차근 채워나가게 됩니다.

최소값(최적의 경우)를 계속 최신화해서 최종 minmult값을 도출하게 됩니다.
그리고 P배열에는 최적의 경우 곱셈의 경계선이 되는 부분이 몇 번째 인지 저장하게 됩니다.

Test Case

pseudo code에 충실하여 code를 구현해보았습니다.

Test Code

W배열
: 교안에 주어진 test case
made배열
: 임의의 자작 데이터

#include <iostream>
#include <vector>
#include <climits>
using namespace std;
int minmult(int n, const vector<int> d, vector<vector<int>>& p);
void order(int i, int j, vector<vector<int>> p);
void print(const vector<vector<int>> v);

int main()
{
	//교안 데이터
	vector<int> d = {5,2,3,4,6,7,8};
	//자작 데이터
	vector<int> made = {2,5,6,2,1,6,3};
	
	vector<int> empty(d.size()); //empty vector를 p vector 초기화에 이용 
	vector<vector<int>> p(d.size(), empty); //최적곱셈순서 출력 도와줄 p 
	cout << "최소 곱셈 횟수 : " << minmult(p.size() - 1, d, p) << endl;
	cout << "최소 곱셈 양식 : "; order(1,6,p); cout << endl << endl;

	cout << "p\n";
	print(p);
	
	vector<int> made_empty(made.size()); //made_empty vector를 made vector 초기화에 이용
	vector<vector<int>> made_p(made.size(), empty);  //최적곱셈순서 출력 도와줄 made_p
	cout << "최소 곱셈 횟수 : " << minmult(made_p.size() - 1, made, made_p) << endl;
	cout << "최소 곱셈 양식 : "; order(1,6,made_p); cout << endl << endl;
	cout << "made_p\n";
	print(made_p);
	
	
	return 0;
}

int minmult(int n, const vector<int> d, vector<vector<int>>& p)
{
	int i, j, k, diagonal,minnum;
	vector<int> empty(n+1);	//pesudo code에 충실하고자 0행 0열 인덱스 이용하지 않음 
	vector<vector<int>> M(n+1, empty);
	//임의의 M vector 생성 후 구하고자 하는 최소곱셈횟수 값인 [1][n] 반환예정 
	
	for(i = 1 ; i <= n ; i++)
	{
		for(k = 1 ; k <= n ; k++)
		{
			M[i][k] = INT_MAX;
		}
	}
	
	for(i = 1 ; i<= n ; i++)
		M[i][i] = 0;
		
	for(diagonal = 1; diagonal <= n-1; diagonal++) //대각 
	{
		for(i = 1 ; i <= n-diagonal ; i++) //대각과 열의 인덱스 합은 항상 n인점 이용 
		{
			j = i + diagonal;
			for(k = i ; k <= j-1 ; k++)	//후보들 계속 비교 
			{
				if(M[i][j] > (M[i][k] + M[k + 1][j] + d[i - 1] * d[k] * d[j]))
				{
					M[i][j] = (M[i][k] + M[k + 1][j] + d[i - 1] * d[k] * d[j]); 					
					minnum = k;
				}
				p[i][j] = minnum;
			}
		}
	}
	print(M);
	return M[1][n];
}

void order(int i, int j, vector<vector<int>> p)
{//재귀 호출로 최소곱셈 양식 출력  
	int k;
	if(i == j) cout << "A" << i;
	else
	{
		k = p[i][j];
		cout << "(";
		order(i,k,p);
		order(k+1,j,p);
		cout << ")";
	}
} 

void print(const vector<vector<int>> v)
{
	for(int i = 0 ; i < v.size() ; i++)
	{
		for(int k = 0 ; k < v[i].size() ; k++)
		{
			if(i == 0 || k == 0)
				continue;
			if(v[i][k] == INT_MAX)
				cout << "  ";
			else
				cout << v[i][k] << " ";	
		}
		cout << endl;
	}
	cout << endl;
 }

Output

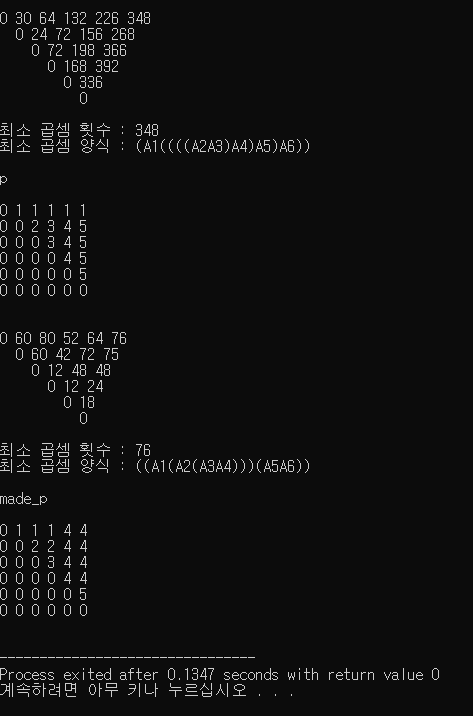
출력 결과는 다음과 같습니다.

감사합니다.