숭실대학교 컴퓨터학부 최지웅 교수님의 강의를 수강하며 학습한 내용입니다.

---

Floyd Algorithm

(플로이드 알고리즘, 플로이드 와샬 알고리즘)

Definition

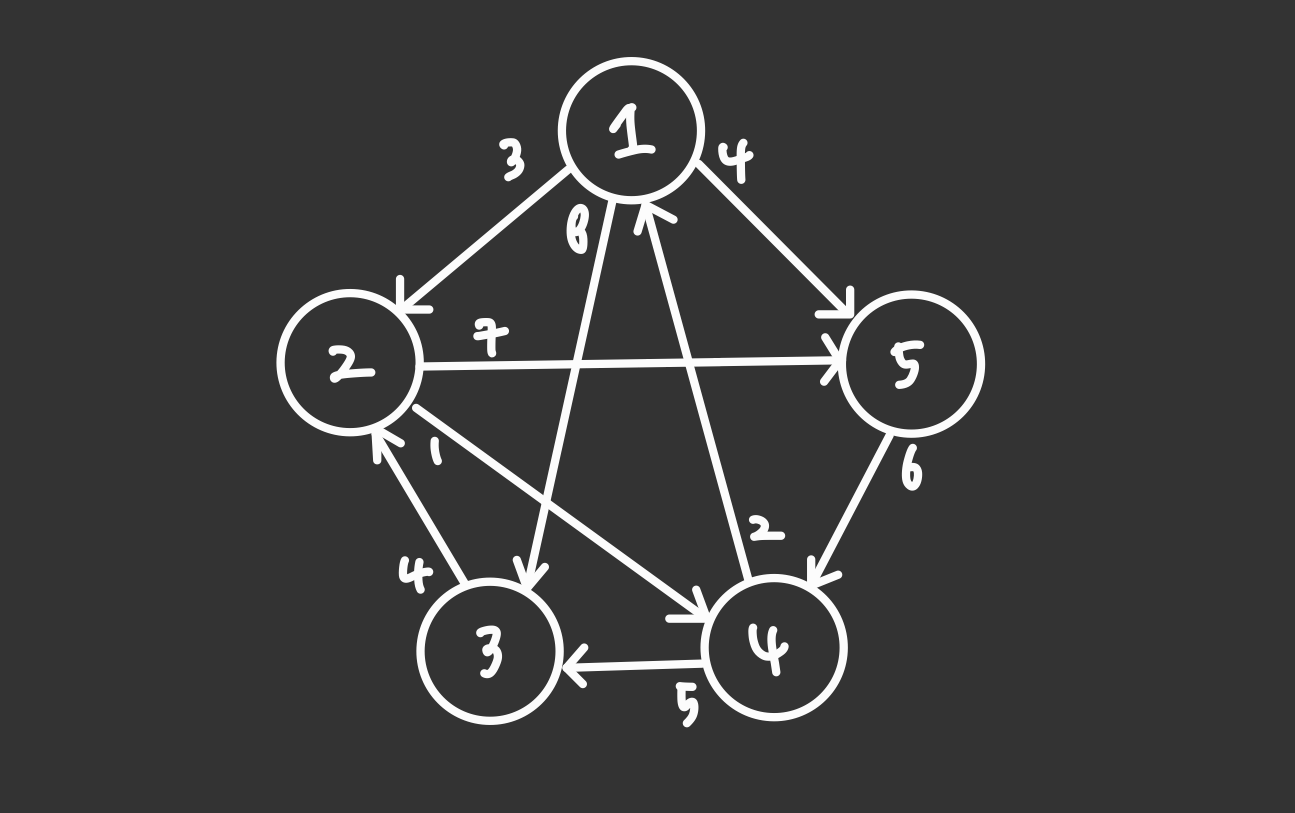
: 정점과 가중치가 있는 그래프에서 정점과 정점사이의 최단거리를 구하는 알고리즘 입니다.

출발지와 정점까지 경유지를 거치는 과정의 경우의 수를 모두 고려하는 특징을 가집니다.

하단에 주어진 문제상황을 참고하도록 하겠습니다.

Problem

문제상황 : 가중치 포함 그래프의 각 정점에서 다른 모든 정점까지의 최단거리를 계산하라.

• 입력
  : 가중치 포함, 방향성 그래프 W와 그 그래프에서의 정점의 수 n
• 출력
  : 최단거리의 길이가 포함된 배열 D

Pseudo Code

void floyd(int n, const number W[][], number D[][])
{
	int i, j, k;
    D = W;
    for(k = 1 ; k <= n ; k++)
    	for(i = 1 ; i <= n ; i++)
        	for(j = 1 ; j <= n ; j++)
            	D[i][j] = minimum(D[i][j], D[i][k]+D[k][j]);
}
//강의 교안에서 참조한 pseudo code 입니다. 

Floyd Algorithm은 Dynamic Programming에 의거합니다.

Code Review

W배열의 인덱스 중 하나를 W[a][b]를 보았을 때 (a<n && b<n), 이 인덱스에는 출발지 정점 Va에서 정점 Vb까지의 가중치가 초기화되어 있는 상태입니다.
(단, 간선이 없는 경우에는 무한대의 값(혹은 임의의 큰 수)가 저장되어 있습니다.)

이를 D배열에 초기화 해주고 3중 for문 루프를 돕니다.

초기 W배열의 값은 현 상황에서의 최단거리라고 볼 수 있습니다.
(경유지 없이 바로 직행하는 (혹은 경유지 없이는 갈 수가 없는) 상태)

이 최단거리의 값과 어느 정점을 경유해서 가는 거리를 비교해가며 최단거리를 계속해서 최신화하게 되는데, 이 때 Dynamic Programming 기술을 활용하게 됩니다.

최단거리를 구하는 방법은 1) 경유지가 있는 경우, 2) 경유지가 없는 경우 총 두 가지로 나눌 수 있습니다.
다음과 같이 전자와 후자를 계속 비교했을 때 비로소 최단거리가 나오게 됩니다.

Va->Vb 기존 최단거리 vs Va->Vc 최단거리 + Vc->Vb 최단거리
(단, a <= c <= b)

정점c를 1~n까지 늘려가며 하나씩 비교를 해주면
최단거리 값을 저장하는 배열 D배열은 기존 최단거리 값을 유지하거나 새로운 최단거리 값으로 계속 초기화 됩니다.

Example

강의 교안의 예시를 참고하여 이해를 돕도록 하겠습니다.

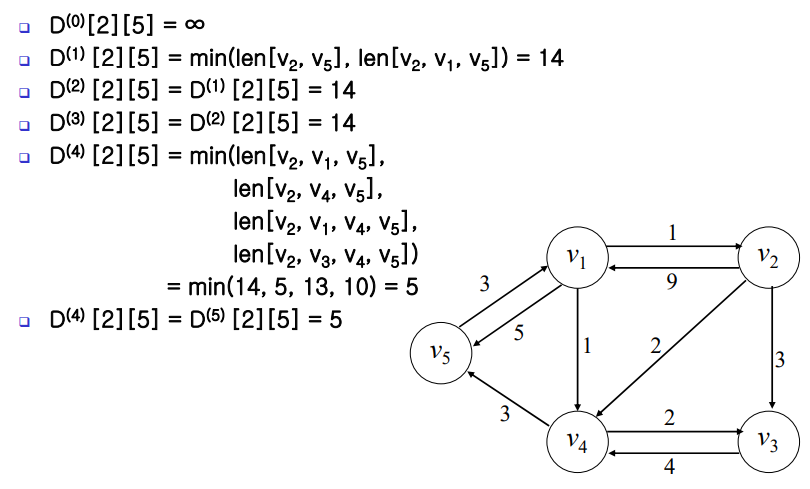
V2->V5 간선이 없는 상황에서 V1~Vn 까지의 정점을 경유하는 경로를 매번 비교하며 최신화 합니다. 새로운 정점을 경유해서 가는 경로가 최단경로가 아니여서 최신화되지 않을 경우, k번째 값을 구하기 위해 k-1번째 값을 참조하는 Dynamic Programming 특성을 이용했습니다.
(단, 1 < k <= n)

Advanced Code

최단거리와 최단경로를 모두 구할 수 있도록 floyd를 다시 구현해보았습니다.

void floyd2(int n, const number W[][], number D[][], index P[][])
{
	index i, j, k;
	for(i=1; i <= n; i++)
		for(j=1; j <= n; j++)
		P[i][j] = 0;
	D = W;
	for(k=1; k<= n; k++)
		for(i=1; i <= n; i++)
			for(j=1; j<=n; j++)
				if (D[i][k] + D[k][j] < D[i][j]) {
					P[i][j] = k;
					D[i][j] = D[i][k] + D[k][j];
				}
}

P배열이 새로 등장하였습니다.
P[a][b]d에는 Va->Vb 최단거리 경로 중 가장 값이 가장 큰 정점의 인덱스가 저장됩니다.

저장된 값들을 Path함수의 재귀적 호출을 이용하여 Va->Vb 최단경로의 경유 정점들을 출력할 수 있습니다.

void path(index q,r)
{
	if (P[q][r] != 0)
    {
		path(q,P[q][r]);
		cout << “ v” << P[q][r];
		path(P[q][r],r);
	}
}

Test Case

pseudo code에 충실하여 code를 구현해보았습니다.

Test Code

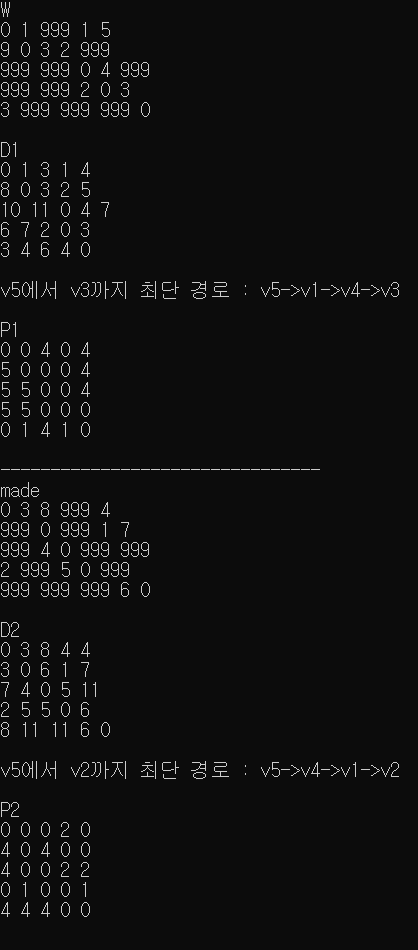
W배열
: 교안에 주어진 test case
made배열
: 임의의 자작 데이터

#include <iostream>
#include <vector>
using namespace std;

void print(const vector<vector<int>> arr)
{//vector 전체출력 함수. W,P1,D2,made,P2,D2 출력 보조  
	for(int i = 1 ; i < arr.size() ; i++)
	{
		for(int j = 1 ; j < arr.at(i).size() ; j++)
		{
			cout << arr.at(i).at(j) << " ";
		}
		cout << endl;
	}
	cout << endl;
	return;
}

void floyd2(int n, const vector<vector<int>> W, vector<vector<int>> &D, vector<vector<int>> &P) 
{//교안의 pseudo code에 충실히 작성. 본인은 c++ library vector를 이용하여 최단경로 알고리즘 구현  
	int i, j, k;
	for(i = 1 ; i < n ; i++)
	{
		for(j = 1 ; j < n ; j++)
		{
			P[i][j] = 0;
		}
	}
	D = W;
	for(k = 1 ; k < n ; k++)
	{
		for(i = 1 ; i < n ; i++)
		{
			for(j = 1 ; j < n ; j++)
			{
				if(D[i][k] + D[k][j] < D[i][j])
				{
					P[i][j] = k;
					D[i][j] = D[i][k] + D[k][j];
				}
			}
		}
	}
}

void path(const int q, const int r, const vector<vector<int>> P)
{//최단경로 출력 알고리즘  
	if(P[q][r] != 0)
	{
		path(q,P[q][r],P);
		cout << "v" << P[q][r] << "->";
		path(P[q][r],r,P);
	}
}

void pathPrinter(const int q, const int r, const vector<vector<int>> P)
{//교안 pseudo code에 충실하게 작성한 path() 의 출력을 간결하게 해줄 pathPrinter 함수  
	cout << "v" << q << "에서 v" << r << "까지 최단 경로 : v" << q << "->";
	path(q, r, P);
	cout << "v" << r << endl<<endl;
}

int main()
{
	//교재 데이터 
	vector<vector<int>> W = { {0,},{0,0,1,999,1,5},{0,9,0,3,2,999},{0,999,999,0,4,999},{0,999,999,2,0,3},{0,3,999,999,999,0} };
	//자작 데이터 
	vector<vector<int>> made = { {0,},{0,0,3,8,999,4},{0,999,0,999,1,7},{0,999,4,0,999,999},{0,2,999,5,0,999},{0,999,999,999,6,0} };
	//pseudo code에 최대한 충실하게 floyd2를 작성하기 위해 0행0열을 비워두고 사용하지 않음.
	//간선이 없음(INF)을 999로 표현
	 
	//빈 배열을 만들어서 D1,P1,D2,P2 초기화에 이용 
	vector<int> empty(W.size());
	
	vector<vector<int>> D1(W.size(), empty);
	vector<vector<int>> P1(W.size(), empty);
	vector<vector<int>> D2(made.size(), empty);
	vector<vector<int>> P2(made.size(), empty);
	
	cout << "W\n";
	print(W);
	floyd2(W.size() , W , D1 , P1);
	
	cout << "D1\n";
	print(D1);
	
	pathPrinter(5,3,P1); //교안에서 test했던 v5 -> v3 최단경로 출력.  
	
	cout << "P1\n";
	print(P1);
	
	cout << "--------------------------------\n";
	
	cout << "made\n";
	print(made);
	floyd2(made.size() , made , D2 , P2);
	
	cout << "D2\n";
	print(D2);
	
	pathPrinter(5,2,P2); //v5 에서 v2까지의 최단경로를 출력하라.  
	cout << "P2\n";
	print(P2);
	
	return 0;
}

Output

출력 결과는 다음과 같습니다.

감사합니다.