오늘 리뷰할 논문은 HOG를 이용한 초기 object detection 알고리즘인 deformable part model (DPM)이다.
논문을 읽었는데 이해는 거의 못해서 리뷰 퀄이 많이 낮다.
아래 포스트를 먼저 읽으면 도움이 될 것이다.

논문은 deformable part, discriminative training, latent SVM을 사용하여 static image에서 generic category의 사물들을 detect하고 localize하는 것을 목표로 한다.
기존에도 사물을 deformable configuration의 부분으로 model하려는 시도가 있었는데 실사용하기는 어려웠다. 어려운 dataset에서 deformable models가 rigid templates나 bag-of-features처럼 “conceptually weaker” models에게 종종 성능이 밀렸기 때문이다.
DPM은 사물 전체를 덮는 하나의 coarse global template와 여러개의 higher resolution part templates를 포함한다. template은 HOG feature를 나타낸다.
models는 discriminatively하게 train하고 semi-supervised이며 feature detection에 의존하지 않고 maxmargin framework로 train된다. 그리고 weakly-labeled data에서 parts를 배우는 간단하고 효과적인 전략을 사용했다.
또 논문은 discriminative training에서 새로운 방법론을 제시한다. part positions 같은 latent variables를 handling하는 SVM을 일반화하고 training 도중 “hard negative” examples를 data mining하는 새로운 방법을 소개한다. 이는 partially labeled data라는 중요한 문제에 도움이 될 것으로 생각한다.
latent SVM은 hidden CRF [19]처럼 nonconvex training problem을 야기하지만 hidden CRF와 달리 latent SVM은 semi-convex이며 latent information이 positive training examples에 대해 specified됐을 때야 training problem이 convex가 된다. 이는 latent SVM이 general coordinate descent algorithm가 되게 한다.
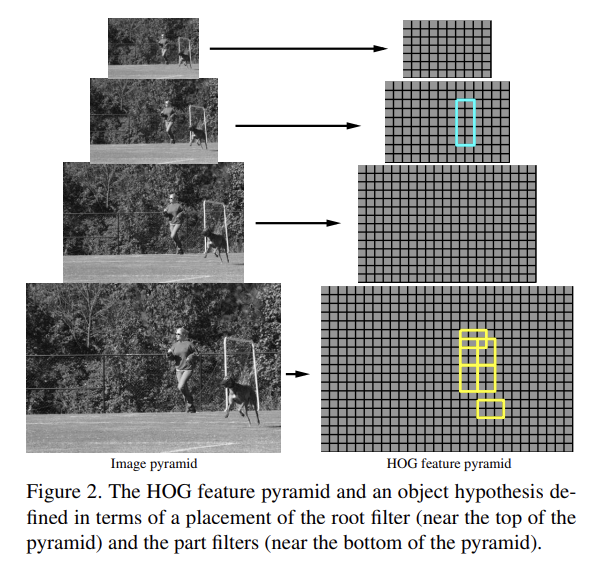
DPM은 scanning window 방식을 사용하며, 하나의 global “root” filter와 여러 part model로 이루어진다. 각 part model은 spatial model과 part filter을 명시한다. spatial model은 detection window에 상대적인 part의 allowed placements의 집합과 각 placement의 deformation cost를 정의한다.
detection window의 score은 window에서 root filter의 점수와 part의 점수의 합이며, 그 part의 placements 중에서 최대값이며, resulting subwindow의 part filter score 빼기 deformation cost를 한 값이다.(뭔소리야?) root filter와 part filters의 score은 window 내의 set of weights와 histogram of gradient (HOG)
features를 dot product하여 구한다. root filter은 Dalal-Triggs model와 동일하다. part filter를 위한 feature은 root filter의 spatial resolution의 2배로 계산된다. 모델은 fixed scale에 정의되며 image pyramid를 따라 검색하는 것으로 사물을 감지한다.
training에서 detection problem을 binary classification problem으로 reduce한다. 각 example x는 다음과 같은 식으로 score된다. beta는 model parameter의 vector이고 z는 part placements 같은 latent values이다.
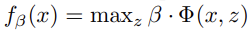
논문은 SVM의 generalization인 latent variable SVM (LSVM)을 고안하는데, positive examples의 latent values를 고정(fix)하면 training problem이 convex가 된다. 이는 coordinate descent algorithm에 사용될 수 있다.
모델은 HOG를 2가지 scale에서 사용한다. 전체 detection window를 덮는 rigid template은 coarse feature을 포착하고 detection window에 관하여 움직일 수 있는 part templates는 finer scale feature를 포착한다. part locations을 위한 spatial model은 coarse template을 reference position으로 삼는 star graph or 1-fan [3]와 동일하다.
특정 resolution에서 이미지의 dense representation를 정의하기 위해 먼저 이미지를 cell이라고 이름붙인 8x8 non-overlapping pixel regions으로 구분한다. 각 cell마다 1D HOG를 구한다. 이 histogram들은 local shape properties를 포착하며 작은 deformation에 대해 invariant하다.
각 cell의 histogram은 인근 2 × 2 blocks의 total gradient energy에 대해 normalize된다. 결과적으로 cell 내의 local gradient information를 나타내는 9 x 4 길이의 vector를 얻게 된다.
Fig 2처럼 standard image pyramid의 각 층의 HOG feature를 계산함으로써 HOG feature pyramid를 정의한다. 피라미드 꼭대기의 feature은 넓은 영역에 걸친 coarse gradients를 포착하고 바닥층은 좁은 영역의 finer gradients를 포착한다.
filter는 HOG pyramid의 subwindows의 weights를 명시하는 rectangular template이다. w x h filter F는 w × h × 9 × 4 weights인 vector다. filter의 score은 weight vector와 HOG pyramid의 w × h subwindow 내의 features를 dot product하여 구한다.
(2.3~3은 세세한 detail과 증명이 너무 많아서 생략하겠다)
논문을 읽었는데 이해는 거의 못해서 리뷰 퀄이 많이 낮다. 옛날 논문이라 그런가 용어도 모르는 게 많고 architecture가 handmade다보니 너무 복잡했다. 중간부터 흥미가 뚝 떨어져서 그냥 skim 리딩했다. 어차피 다시 읽어도 이해 못할 것 같다...

별개로 중간에 여백이 부족해 증명을 생략한다는 문장을 보고 논문인데 이래도 되나 싶어서 벙쪘다. 페르마를 패러디한 걸지도.