오늘 리뷰할 논문은 LSGAN 논문이다.
아래 포스트를 먼저 보면 도움이 될 것이다.
- [LSGAN] Least Squares Generative Adversarial Netorks 논문 정리
- LSGAN 논문 리뷰 - Least Squares Generative Adversarial Networks (ICCV2017)
Summary
기존의 일반적인 GANs는 discriminator에 sigmoid cross entropy loss function를 사용한다. 하지만 이 loss function은 generator을 (real data에서 여전히 멀지만 decision boundary의 correct side에 위치한) fake samples를 이용해 update할 때 vanishing gradients 문제를 일으킨다.
따라서 논문은 discriminator에 least squares loss function를 사용하는 Least Squares Generative Adversarial Networks (LSGANs)를 제안한다. 이는 간단하지만 강력한 방법인데, leasut squares loss는 fake samples를 penalize해서 decision boundary를 향해 이동시킬 수 있기 때문이다. 이 특성에서 기인해 LSGANs는 더 real data에 가까운 samples을 생성할 수 있다.
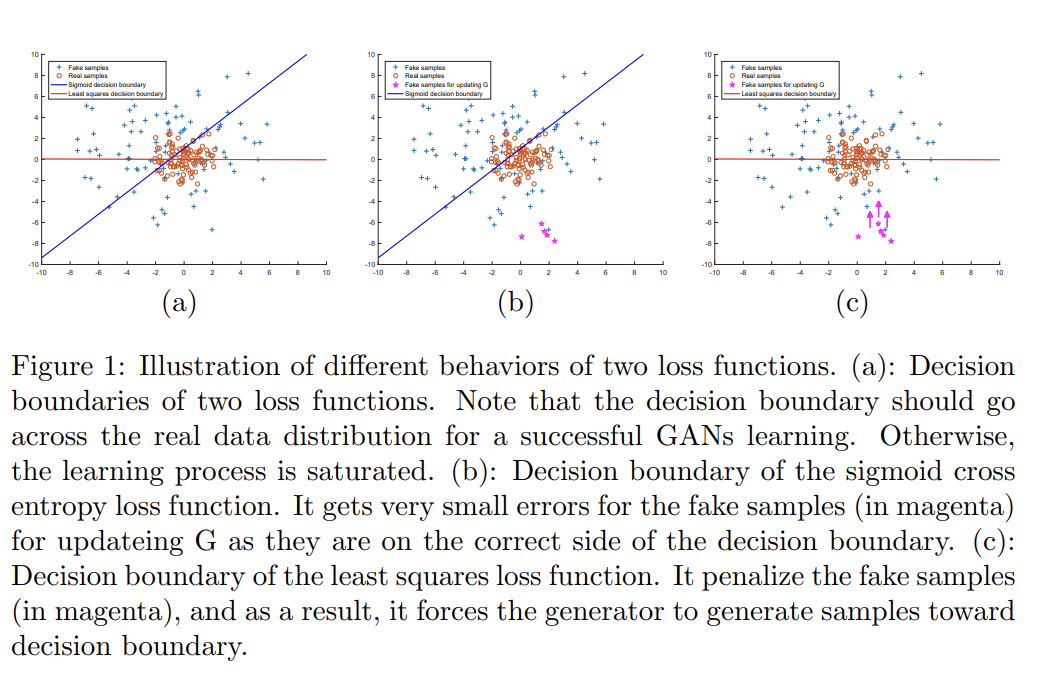
LSGANs의 또 다른 장점은 학습의 향상된 안정성이다. 기존의 GANs는 learning instability에 시달렸고 여러 논문이 objective function을 문제의 원인으로 꼽았다. vanishing gradients이 generator의 update를 어렵게 하기 때문이다. 반면 LSGANs는 이 문제를 완화할 수 있는데, decision boundary까지의 거리를 바탕으로 samples을 penalize하기 때문이다.
논문의 기여는 다음과 같다.
- LSGANs의 objective function을 최소화하는 것이 Pearson divergence를 최소화하는 것과 같음을 보인다. 실험 결과 LSGANs가 더 realistic한 image를 생성할 수 있음을 보인다. LSGANs의 안정성을 증명하는 여러 실험을 수행한다.
- 두 network architecture을 설계했다. 첫째는 여러 scene datasets에 평가되는 112 × 112 resolution image generation이다. 실험 결과 현재(당시) SOTA보다 higher quality images를 생성할 수 있다. 둘째는 많은 classes를 가진 task를 위한 architecture다. 3470 classes를 가진 handwritten Chinese character dataset에 평가하여 모델이 readable characters를 생성할 수 있음을 보였다.
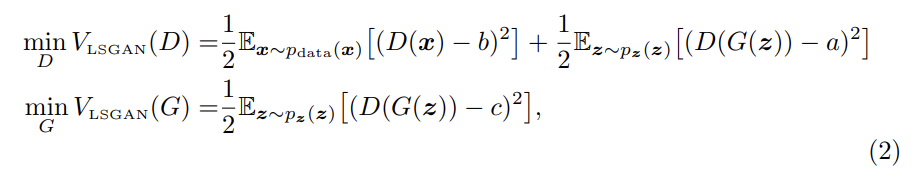
LSGANs의 objective은 위와 같다. discriminator에 a-b coding scheme을 사용했다. a, b는 각각 fake data와 real data에 대한 label이고 c는 G 입장에서 D가 진짜라고 믿게 하고 싶은 fake data다.
LSGANs는 두 가지 장점이 있다. 첫째로 decision boundary의 correct side에 위치한(lie in a long way) samples에 loss를 거의 생산하지 않는 기존의 GANs와 달리 LSGANs는 (심지어 correctly classify되었더라도) 그 samples를 penalize한다. generator을 update할 때 discriminator의 parameters가 수정되서, 즉 decision boundary가 수정되서 generator가 decision boundary를 향해(toward) samples을 생성하게 한다. 한편 성공적인 학습을 위해서 decision boundary가 real data의 manifold에 걸쳐야(go across) 하는데, 그렇지 않으면 learning process가 saturate하기 때문이다. 따라서 generated samples를 decision boundary로 향하게 하는 것이 sample들이 real data manifold에 가깝게 한다.
둘째로 decision boundary의 긴 방향에 놓인(lying a long way to) samples를 penalize하는 것은 generator을 update할 때 더 많은 gradients를 생성할 수 있어 vanishing gradients 문제를 완화하여 learning process를 안정시킨다.
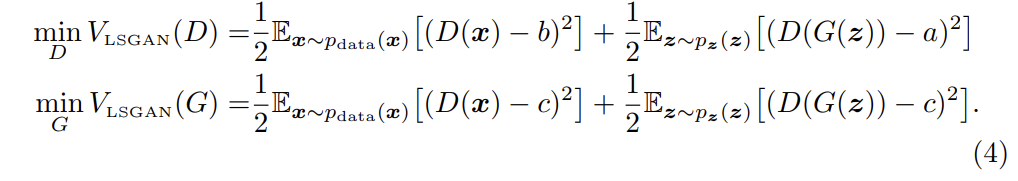
원본 GANs 논문에서는 objective을 최소화하는 것이 Jensen-Shannon divergence를 최소화하는 것과 동일함을 보였는데, 이 논문에선 LSGANs objective와 f-divergence의 관계를 탐구한다.
식 (4)는 식 (2)에서 항 하나를 추가한 것이다. 이때 항이 G의 parameters를 포함하지 않기 때문에 항을 추가해도 optimal values이 바뀌지 않는다.
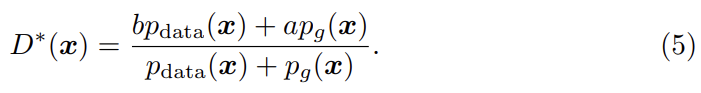
fixed G에 대해 optimal discriminator D를 얻으면 위와 같다. 식 (4)를 다음과 같이 재구성할 수 있다. (표기 편의 상 )
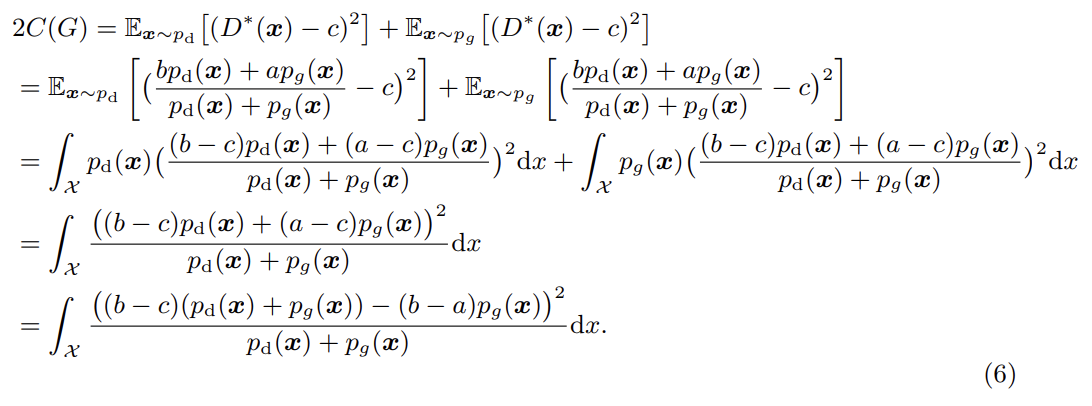
b-c=1, b-a=2로 두면 다음과 같다.
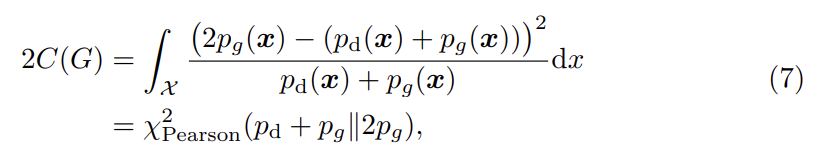
따라서 b-c=1, b-a=2라는 조건 하에 식 (4)를 최소화하는 것이 와 사이 Pearson divergence를 최소화하는 것과 같다.
parameter selection의 경우, 위의 조건을 만족하도록 a = −1, b = 1, c = 0로 두어 아래와 같은 objective function을 사용할 수 있다.
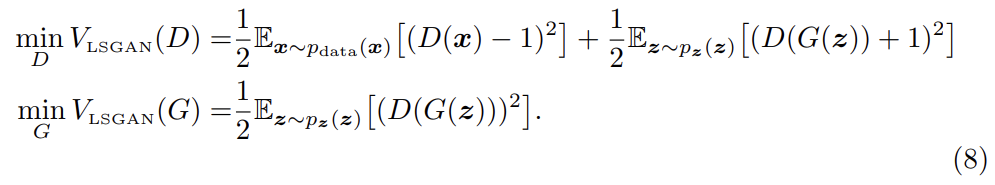
아니면 c=b로 두어 G가 생성하는 sample이 최대한 실제와 가깝게 만들 수도 있다. 예를 들어 0-1 binary coding scheme을 사용해서 다음과 같이 objective function을 사용할 수 있다.
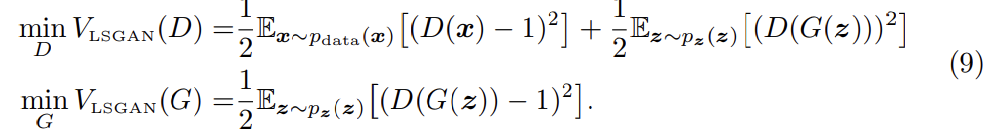
실제로는 식 (8), 식 (9)가 비슷한 성능을 보였다고 한다. 논문에서는 식 (9)를 사용해 학습했다.
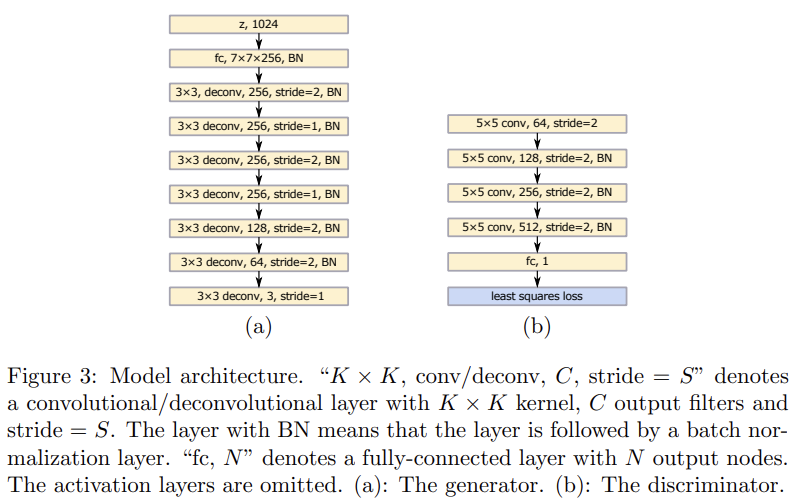
architecture은 Fig 3과 같으며 VGG model에서 영감을 받았다. DCGANs와 비교해 두 stride=1 deconvolutional layers가 꼭대기 두 deconvolutional layers 이후에 추가되었다. discriminator은 least squares loss function을 사용하는 것만 빼면 DCGANs의 architecture과 동일하다. DCGANs처럼 generator, discriminator에 각각 ReLU activations와 LeakyReLU activations을 사용한다.

두번째 모델은 많은 classes를 가진 task를 위한 모델이다. 논문은 먼저 large label vectors를 small vectors로 map하는 linear mapping layer를 사용하고 이후에 small vectors를 layers로 concatenate하는 방식을 이용한다. Fig 4에 architecture가 나타나 있으며 어떤 layer에 concatenate할지는 경험적으로 선택했다. objective function은 아래와 같으며 는 linear mapping function, y는 label vectors다.
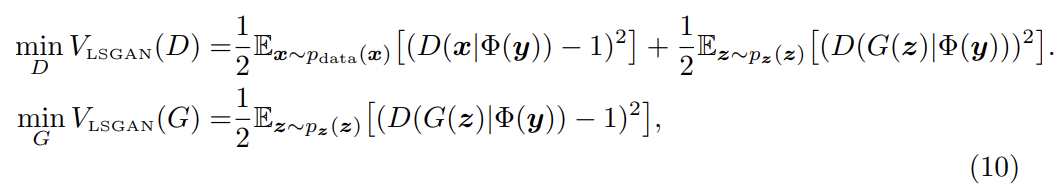
실험은 두 데이터셋 LSUN, HWDB1.0을 이용했다.
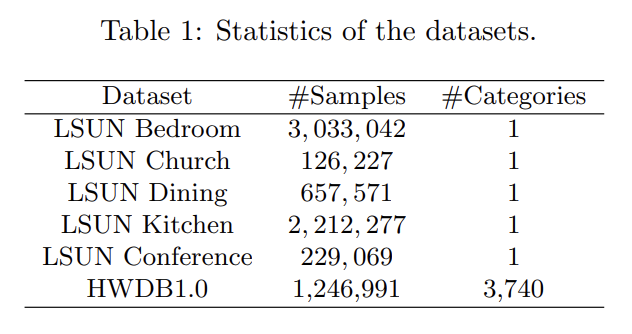


Fig 3의 LSGANs을 LSUN의 다섯 scene datasets인 bedroom, kitchen, church, dining room, conference room에 학습시켰다. Fig 5는 bedroom에 대해 LSGANs과 baseline인 DCGANs, EBGANs의 결과를 보여준다. LSGANs의 퀄리티가 다른 두 baseline보다 좋음을 볼 수 있다.

또 LSGANs의 향상된 stability를 보이기 위해 두 가지 비교 실험을 한다. 비교를 위해 DCGANs에 기반한 두 가지 architecture을 디자인한다. 첫째는 generator에서 batch normalization를 제외한 모델이고 둘째는 generator과 discriminator 모두 batch normalization을 제외한 모델이다. model performance에 optimizer 선택이 몹시 중요하기 때문에 두 architecture을 두 optimizer, Adam과 RMSProp에 실험한다. 이 네가지 세팅을 가지고 LSUN bedroom dataset에 regular GANs과 LSGANs를 각각 학습한다.
실험 결과 네 가지를 알 수 있었다. 1. + Adam 조합은 10번 중 5번 좋은 quality image를 생성했다. 하지만 regular GANs은 상당한 수준의 mode collapse에 시달리고 successful learning이 불가능했다. 2. + RMSProp 조합은 LSGANs이 (약간의 mode collapse를 보이는) regular GANs보다 higher quality images를 생성했다. 3. + RMSProp과 + Adam은 LSGANs과 regular GANs의 성능이 비슷했다. + RMSProp은 LSGANs과 regular GANs 모두 data distribution을 성공적으로 학습했고 + Adam은 둘 다 약간의 mode collapse를 보였다. 4. RMSProp이 Adam보다 더 안정적으로 작동했다. 에서 regular GANs은 RMSProp로는 data distribution 학습에 성공했지만 Adam으로는 실패했기 때문이다.
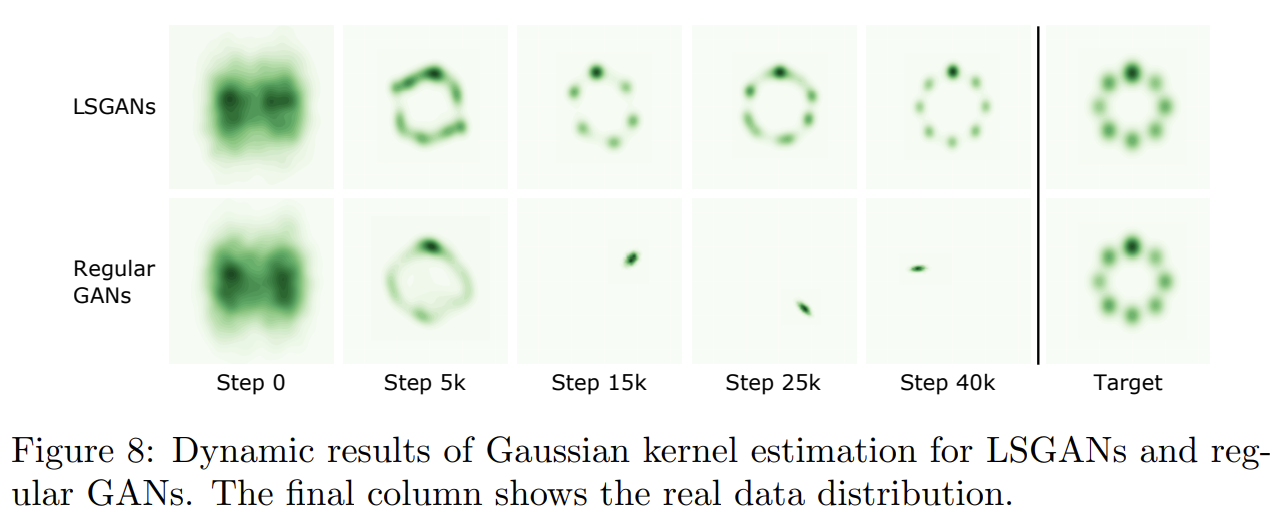
두 번째 실험은 Gaussian mixture distribution dataset에 평가한 것이다. generator와 discriminator가 모두 3 fully-connected layers를 포함하는 간단한 architecture를 사용해서 2D mixture of 8 Gaussian dataset에 LSGANs와 regular GANs를 학습한다. Fig 8은 Gaussian kernel density estimation의 dynamic results를 보여준다. regular GANs가 step 15k부터 mode collapse를 겪어 data distribution의 single valid mode 주위로 sample을 생성함을 알 수 있다. 반면 LSGANs은 Gaussian mixture distribution을 성공적으로 학습한다.

Fig 4의 conditional LSGAN model을 3470 classes를 가진 handwritten Chinese character dataset에 학습한다. LSGANs는 readable Chinese characters를 성공적으로 생성했다. label vectors로 생성된 이미지의 correct label을 얻을 수 있으므로 이후에 data augmentation에 적용될 수도 있다.
Strengths
- 기존의 Sigmoid cross entropy loss가 아니라 least squares를 사용한 점이 인상적이었다.
Weaknesses
- 실험에 정성 평가 밖에 하지 못했다. baseline보다 좋다는 것을 정량적으로 증명할 수 없었다.