오늘 리뷰할 논문은 SNGAN 논문이다. 논문이 거의 수학이라 이해도가 많이 낮다.
아래 포스트를 먼저 읽으면 도움이 될 것이다.
- [논문 Summary] SNGAN (2018 ICLR) "Spectral Normalization for Generative Adversarial Networks"
- Spectral Normalization for Generative Adversarial Networks(SN-GAN) - (1)
Summary
GAN의 고질적인 문제는 discriminator의 performance control이다. high dimensional space에서 training 중 discriminator에 의한 density ratio estimation은 종종 부정확하고 unstable하며 generator은 target distribution의 multimodal structure을 배우는데 실패한다. 심지어 더 나쁜 경우는 model distribution의 support와 target distribution의 support가 disjoint할 때 model distribution과 target을 완벽히 구분할 수 있는 discriminator가 존재한다는 것이다. 이 경우 discriminaot에 의한 기울기가 0이 되기 때문에 generator의 학습이 완전히 멈춰 버린다.
따라서 논문은 discriminator의 학습을 안정화하는, spectral normalization이라고 이름 붙인 새로운 weight normalization을 제안한다. 이 normalization은 두 특징을 만족한다.
- Lipschitz constant가 tune할 유일한 parameter고 알고리즘이 intensive tuning를 필요로 하지 않는다.
- 구현이 간단하고 추가 연산 비용이 적다.
논문은 spectral normalization의 효과를 다른 regularization 기술인 weight normalization, weight clipping, gradient penalty과 비교한다. 또한 complimentary regularization techniques(batch normalization, weight decay, feature matching on the discriminator)가 없는 상황에서 spectral normalization이 weight normalization과 gradient penalty보다 생성된 이미지의 퀄리티를 향상시킴을 보인다.
최근 연구들은 discriminator가 선택된 function space가 GAN의 성능에 중요하다는 것에 집중한다. 여러 연구가 boundedness of statistics를 보장하는 Lipschitz continuity의 중요성을 지지한다. 예를 들어 일반적인 GAN에서 optimal discriminator의 식과 도함수는 아래와 같은데, 도함수는 unbounded거나 심지어 incomputable일 수도 있다.
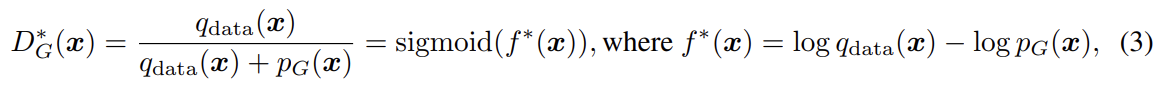
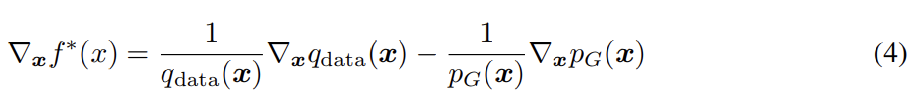
이는 f의 도함수에 어떤 regularity condition을 도입하도록 촉구한다. 그런 맥락에서 성공적이었던 한 연구는 input에 대한 regularization terms을 추가해 discriminator의 Lipschitz constant을 조절했다. 논문도 그들처럼 set of K-Lipschitz continuous functions에서 discriminator D를 찾는다.

는 임의의 x, x'와 L2 norm에 대해 을 만족하는 최소의 M이다. (기존 연구의) input에 기반한 regularization은 generator와 data distribution의 support의 바깥 space에 regularization을 부과할 수 없다는 단점이 있다. 이 논문에서 제안하는 spectral normlization은 Yoshida & Miyato (2017)가 고안한 기술을 통해 weight matrice를 normalize해서 이 문제를 회피한다.
spectral normlization은 각 layer g : 의 spectral norm을 제한하는 것으로 discriminator function f의 Lipschitz constant를 조절한다. 정의에 따라 Lipschitz norm 는 와 동일한데 여기서 σ(A)는 matrix A의 spectral norm이다(L2 matrix norm of A).
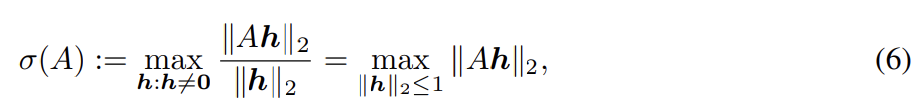
이는 A의 largest singular value와 동일하다. 따라서 linear layer g(h) = Wh에 대해 norm은 로 주어진다. activation function 의 Lipschitz norm이 1과 같다면 부등식 를 사용해서 다음과 같이 의 bound를 찾을 수 있다.
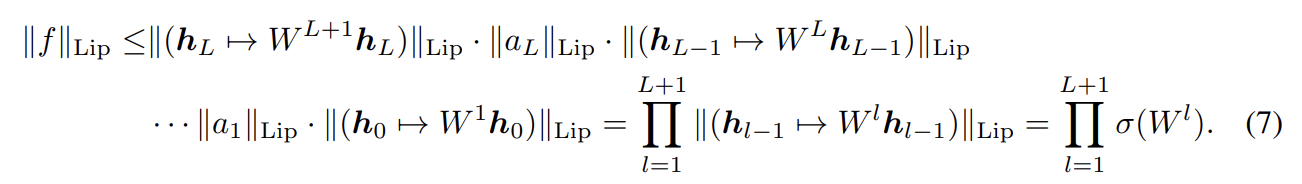
spectral normlization은 weight matrix W의 spectral norm을 normalize하여 Lipschitz constraint σ(W) = 1을 만족하게 한다.

식 (8)로 각 을 normalize하면 부등식 (7)과 라는 사실에 의해 가 1로 bound됨을 알 수 있다.
discriminator의 각 layer을 regularize하기 위해 사용한 spectral norm σ(W)는 W의 largest singular value이다. 그런데 이를 계산하기 위해 SVD를 적용하면 알고리즘이 너무 연산 비용이 많이 든다. 따라서 σ(W)를 추정하기 위해 power iteration method(Golub & Van der Vorst, 2000; Yoshida & Miyato, 2017)를 사용한다. 이를 통해 적은 추가 연산 비용으로 spectral norm을 추정할 수 있다.
에 대한 의 gradient는 다음과 같다.
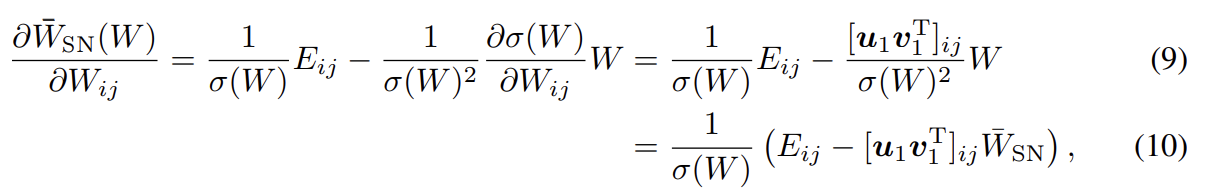
이때 는 (i,j)-th entry가 1이고 나머지는 0인 행렬이며 u1, v1은 각각 W의 first left, right singular vector이다. h가 에 의해 변환될 hidden layer이라면 mini-batc에서 V(G, D)의 미분은 다음과 같이 주어진다.
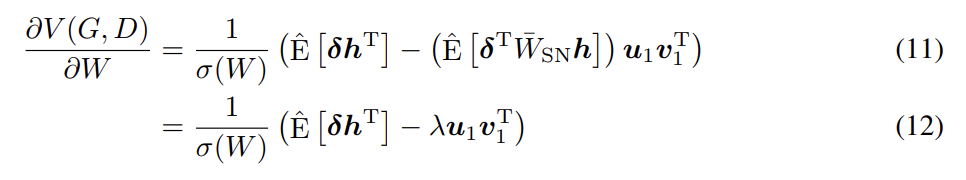
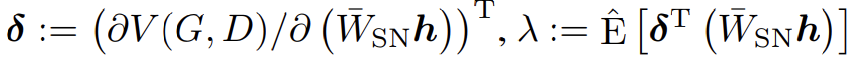
는 mini-batch에서 empirical expectation이고 어떤 에 대해 일 때 이 된다. 식 (12)의 첫번째 항 는 normalization 없는 weights의 derivative과 같다. 두 번째 항은 adaptive regularization coefficient λ를 가지고 first singular components를 penalizing하는 regularization term으로 생각할 수 있다. δ와 가 비슷한 방향을 가리킬 때 λ는 양수고 이는 training 도중 W의 column space가 한 방향으로 집중되는 것을 예방한다. 다시 말해 spectral normalization은 각 layer이 한 방향으로 민감해지는 변형을 방지한다. 또 model에 새로운 parameterization을 고안하기 위해 spectral normalization을 사용할 수 있다. 즉 layer map을 두 trainable component인 spectrally normalized map와 spectral norm constant로 구분할 수 있다.
(3 SPECTRAL NORMALIZATION VS OTHER REGULARIZATION TECHNIQUES 생략)
실험은 CIFAR-10과 STL-10에 unsupervised image generation을 한다. 큰 dataset에도 잘 작동하는지 확인하고자 ILSVRC2012 dataset (ImageNet)에도 적용한다.
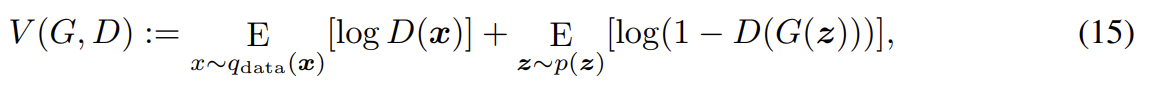
adversarial loss는 식 (15)를 사용했다. 또 discriminator과 generator 각각에 다음과 같이 hinge loss를 이용해 알고리즘의 성능을 평가했다.
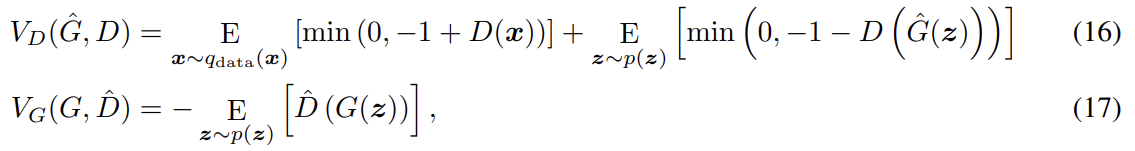
이 objectives를 최적화하는 것은 reverse KL divergence : 를 최소화하는 것과 같다. 생성된 이미지의 양적 평가를 위해 inception score와 Frechet inception distance (FID)를 사용했다. hinge loss에 기반한 알고리즘은 inception score와 FID로 평가할 때도 좋은 성능을 보였다.
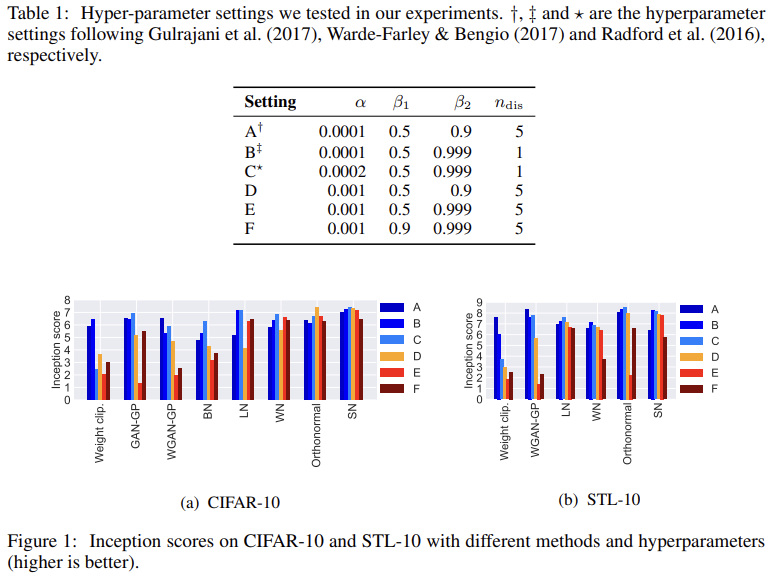
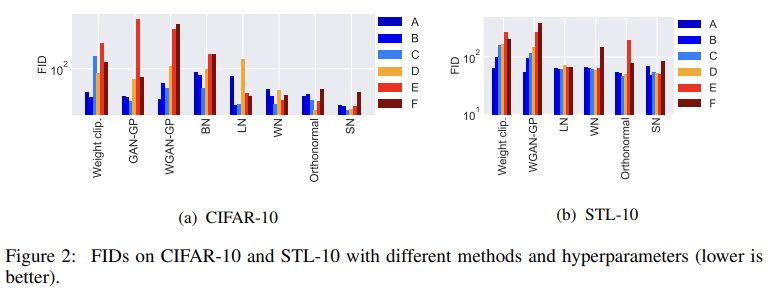
Fig 1, 2는 세팅 A~F에서 각 방법의 inception score와 FID를 보여준다. spectral normalization이 aggressive learning rates와 momentum parameters에 robust함을 볼 수 있다.
(이하 실험 생략)