링크텍스트
마을을 두 개의 분리된 마을로 분할하고(각 마을에는 1개 이상의 집이 있어야 함) 분리된 두 마을 안에서의 길의 유지비의 합은 최소화한다. 이때 유지비가 얼마인지 구하는 문제이다.
결국 최소 신장 트리를 구하고 이 안에서의 가중치의 합을 구하면 된다.
프림 알고리즘을 통해서도 구할 수 있지만 나는 크루스칼 알고리즘을 통해 구해보았다. 크루스칼 알고리즘을 외워버렸더니 쉽게 풀 수 있는 문제였다.
최소 신장 트리를 구한 후, 가장 마지막에 추가된 간선(트리의 간선 중 가장 가중치가 큼)을 지워준 다음, 간선들의 가중치 합을 구하면 된다.
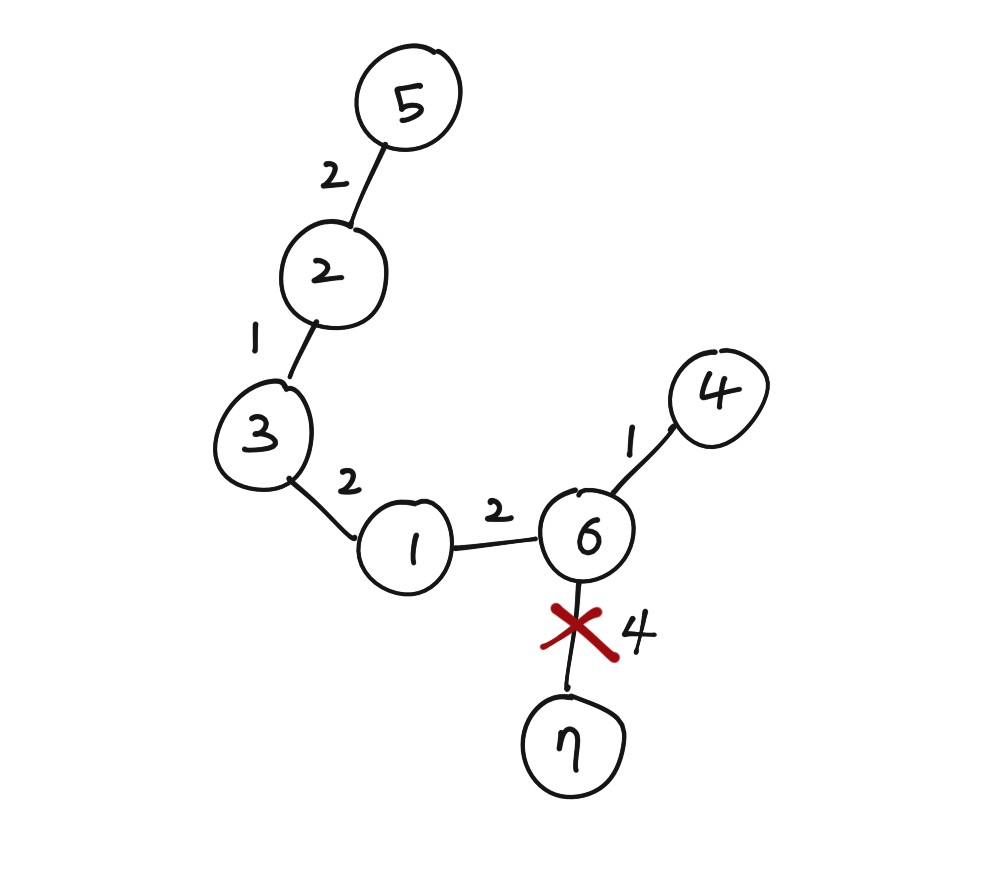
예를 들어 최종 최소 신장 트리가 이렇게 만들어졌다면, 여기서 가장 큰 가중치의 간선을 없애야 모든 가중치의 합이 최소가 될 수 있다.
집 5, 2, 3, 1, 6, 4로 이루어져 있는 마을 하나와 집 7 한 채로 이루어져 있는 마을 하나로 분리되게 되는 것이다.
n, m = map(int, input().split()) # n: 집의 개수
edges = []
for _ in range(m):
a, b, cost = map(int, input().split())
edges.append((cost, a, b))
parent = [i for i in range(n+1)]
def find_parent(x):
if parent[x] != x:
parent[x] = find_parent(parent[x])
return parent[x]
def union_parent(a, b):
a = find_parent(a)
b = find_parent(b)
if a < b:
parent[b] = a
else:
parent[a] = b
def kruskal(n, edges):
edges.sort() # 오름차순 정렬
used_edges = 0
for cost, idx, adj in edges:
if find_parent(idx) != find_parent(adj):
if used_edges == n-1: break
union_parent(idx, adj)
temp.append((cost, idx, adj)) # 트리에 연결된 간선 추가
used_edges += 1
return result
print(kruskal(n, edges) - temp[-1][0]) # 트리 중 가중치가 가장 큰 값의 간선 제거
