모든 행성을 연결했을 때, 최소 플로우의 관리비용을 출력하는 문제이다.
즉, 트리의 모든 노드를 연결했을 때, 간선들의 가중치의 합이 최소가 되도록 해야 한다.
결국 최소 신장 트리의 가중치의 합을 구하면 되고 이는 프림 알고리즘이나 크루스칼 알고리즘을 적용해 해결할 수 있다.
주어진 입력값인 인접 행렬(Adjacency Matrix) 형태에서
간선의 정보 형태: (가중치, 노드1, 노드2)의 형태로 만들어준다.
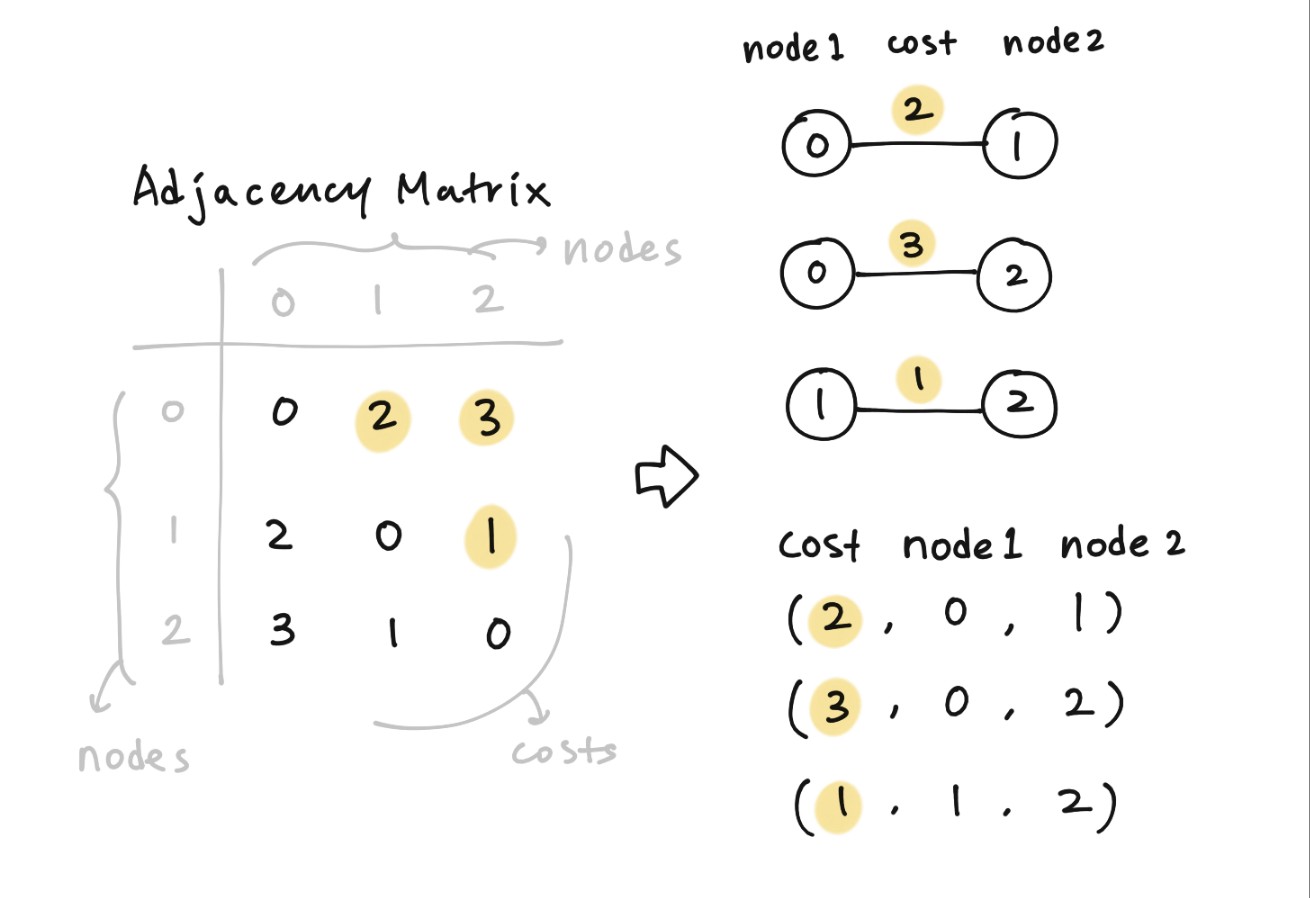
3 # n: 행성(노드)의 수
0 2 3 # 인접 행렬
2 0 1
3 1 0
-> edges: [(2, 0, 1), (3, 0, 2), (1, 1, 2)]
n = int(input())
input_list = [list(map(int, input().split())) for _ in range(n)]
# [[0, 2, 3], [2, 0, 1], [3, 1, 0]]
edges = []
for a in range(n):
for b in range(a+1, n):
edges.append((input_list[a][b], a, b))
# input_list[0][1], 0, 1
# input_list[0][2], 0, 2
# input_list[1][2], 1, 2이렇게 만들어진 간선의 정보들(edges)을 가지고 최소 신장 트리를 만들면 된다.
1. 프림 알고리즘
* 힙을 사용한다.
[작동 순서]
1. 임의의 노드를 시작으로 선택한다.
2. 해당 노드와 연결된 간선을 탐색 대상에 추가한다.
3. 탐색 대상에서 가장 가중치가 낮은 간선을 뽑는다. (힙)
간선의 끝 점이 아직 방문하지 않았다면, 그 간선을 추가한다.
방문했다면, 방문하지 않은 간선이 나올 때까지 간선을 뽑는다.
4. 새로 추가된 노드와 연결된 간선을 탐색 대상에 추가한다.
5. 3~4번 과정을 (전체 노드 수-1)개의 간선이 트리에 추가될 때까지 반복한다.
import heapq
def prim(n, edges):
# n: 노드의 개수
# edges (가중치, 현재 노드, 연결되어 있는 노드)의 리스트
# edges (cost, idx, adj)의 리스트
# 최소 신장 트리의 가중치를 반환한다.
# 방향이 없는 인접 리스트를 만든다.
graph = [[] for _ in range(n+1)]
for cost, node1, node2 in edges:
graph[idx].append((cost, adj))
graph[adj].append((cost, idx))
# [[(2, 1), (3, 2)], [(2, 0), (1, 2)], [(3, 0), (1, 1)], []]
# 노드를 추가했다는 것을 표시
visited = [False] * (n+1)
# 임의의 노드를 시작으로 선택한다. (1로 선택)
visited[1] = True
heap = []
# 해당 노드와 연결되어 있는 노드들 힙에 push.
for cost, adj in graph[1]:
heapq.heappush(heap, (cost, adj))
result = 0 # 최소 신장 트리의 가중치의 합
used_edges = 0
while used_edges < n-1: # 트리가 완성될 때까지 (n-1개의 간선을 다 사용할때까지)
cost, idx = heapq.heappop(heap) # 가중치가 낮은 간선을 선택
if visited[idx]:
continue
visited[idx] = True
result += cost
used_edges += 1
# 선택한 노드와 연결된 간선들을 큐에 넣는다.
for idx_cost, adj in graph[idx]:
if not visited[adj]:
heapq.heappush(heap, (idx_cost, adj))
return result
print(prim(n, edges))2. 크루스칼 알고리즘
작동 순서
1. 모든 간선들을 가중치에 대해 오름차순으로 정렬한다.
2. 앞에서부터, 간선을 트리에 추가했을 때, 사이클이 생기지 않는다면 그 간선을 트리에 추가한다.
사이클이 생긴다면 간선을 트리에 추가하지 않고 넘어간다.
사이클이 생겼는지 알 수 있는 방법: 부모의 노드를 찾는 find 함수와 서로 다른 부모 노드를 가지는 집합들을 합치는 union 함수를 통해 판단한다.
3. 2번 과정을 (전체 노드 수-1)개의 간선이 트리에 추가될 때까지 반복한다.
parent = [i for i in range(n+1)] # 부모 노드들을 각자 노드들로 초기화
# 부모 노드를 찾는 함수
def find_parent(x):
if parent[x] != x:
parent[x] = find_parent(parent[x])
return parent[x]
# 부모 노드를 합치는 함수
def union_parent(a, b):
a = find_parent(a)
b = find_parent(b)
if a < b: # 더 작은 쪽으로 부모를 합침
parent[b] = a
else:
parent[a] = b
def kruskal(n, edges):
# n: 노드의 개수
# edges (가중치, 현재 노드, 연결되어 있는 노드)의 리스트
# edges (cost, idx, adj)의 리스트
# 최소 신장 트리의 가중치를 반환한다.
edges.sort() # 오름차순(가중치가 작은 순서) 으로 정렬
result = 0 # 가중치의 합
used_edges = 0
for cost, idx, adj in edges:
if find_parent(idx) != find_parent(adj): # 부모가 같지 않으면(사이클이 생기지 않는다면)
if used_edges == n-1: break
union_parent(idx, adj) # 간선을 트리에 추가
result += cost
used_edges += 1
return result
print(kruskal(n, edges))