수강해야 하는 강의 수와 전제 조건 리스트가 주어졌을 때, 모든 강의를 수강할 수 있는 상태인지 알아보는 문제이다.
전제 조건이란,
예를 들어, [0, 1] 로 표시되어 있다면 강의 0을 수강하기 위해서는 반드시 강의 1을 수강해야 함을 의미한다.
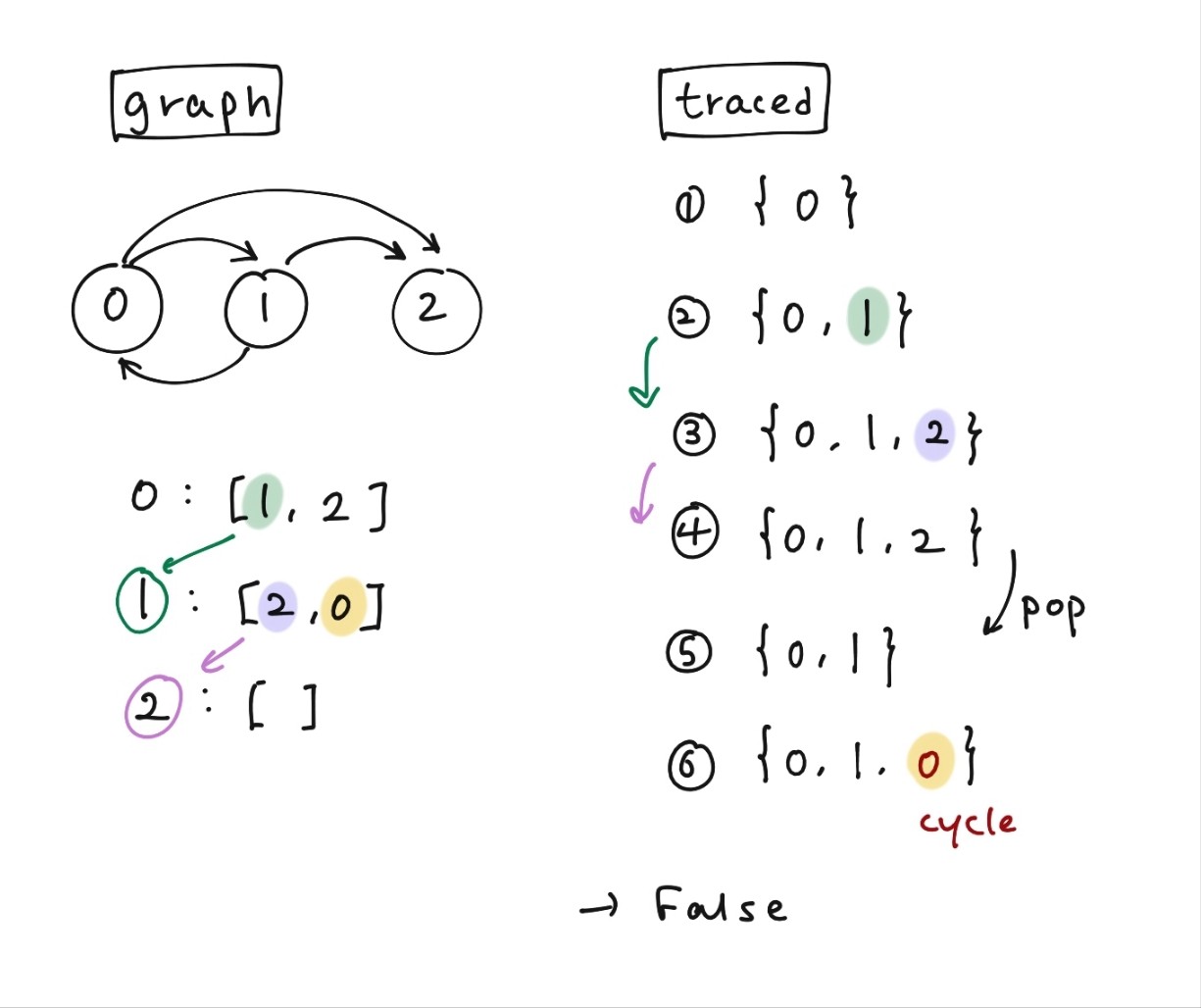
만약 2개의 강의를 들어야 하며 전제 조건이 [1, 0], [0, 1]라면, 강의 1을 수강하기 위해서는 강의 0을 먼저 수강해야 하는데, 강의 0을 수강하기 위해서는 강의 1을 수강해야 하므로 불가능한 코스 스케줄이다.
이를 그래프로 나타내보면 다음과 같고 이 그래프에서는 사이클이 존재하는 것을 알 수 있다.
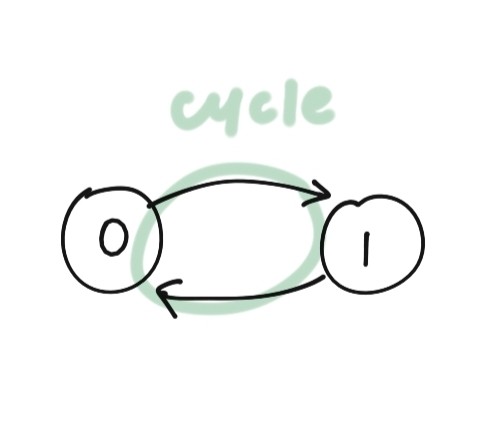
그러므로, 이 문제를 풀기 위해서는 그래프에서 사이클의 존재 여부를 확인하면 된다.
# numCourses = 3 # 강의 수
# prerequisites = [[0, 1],[0, 2],[1, 0], [1, 2]] # 전제 조건
# 1. directed graph 만들기 (방향이 있는 그래프)
graph = defaultdict(list)
for a, b in prerequisties:
graph[a].append(b)
# graph: {a: [b1, b2], ... }
# ex) {0: [1, 2], 1: [0, 2], 2: []}
# 2. graph에 사이클이 존재하는지 확인하기
# 사이클이 존재하는지 판별하기 위해 앞서 방문했던 노드를 traced에 저장
# 이미 방문한 곳을 또 방문하게 된다면 사이클이 존재한다고 판별
traced = set()
visited = set()
# dfs를 통해 graph 탐색
def dfs(i):
if i in traced: # 현재 노드가 traced에 이미 있다면 사이클이 있다고 판정
return False # False 반환
if i in visited: # 이미 방문했던 노드라면
return True # 더 이상 진행하지 않고 True 반환
traced.add(i) # 현재 노드 방문
for b in graph[i]: # 현재 노드(a)에 연결된 노드들(b1, b2, ...) 중에
if not dfs(b): # 사이클이 있다고 판정되면
return False # False 반환
traced.remove(i) # 방문 후 현재 노드 삭제
return True # 사이클이 없는 경우 True 반환
그림 예시)
1. 사이클이 없는 경우
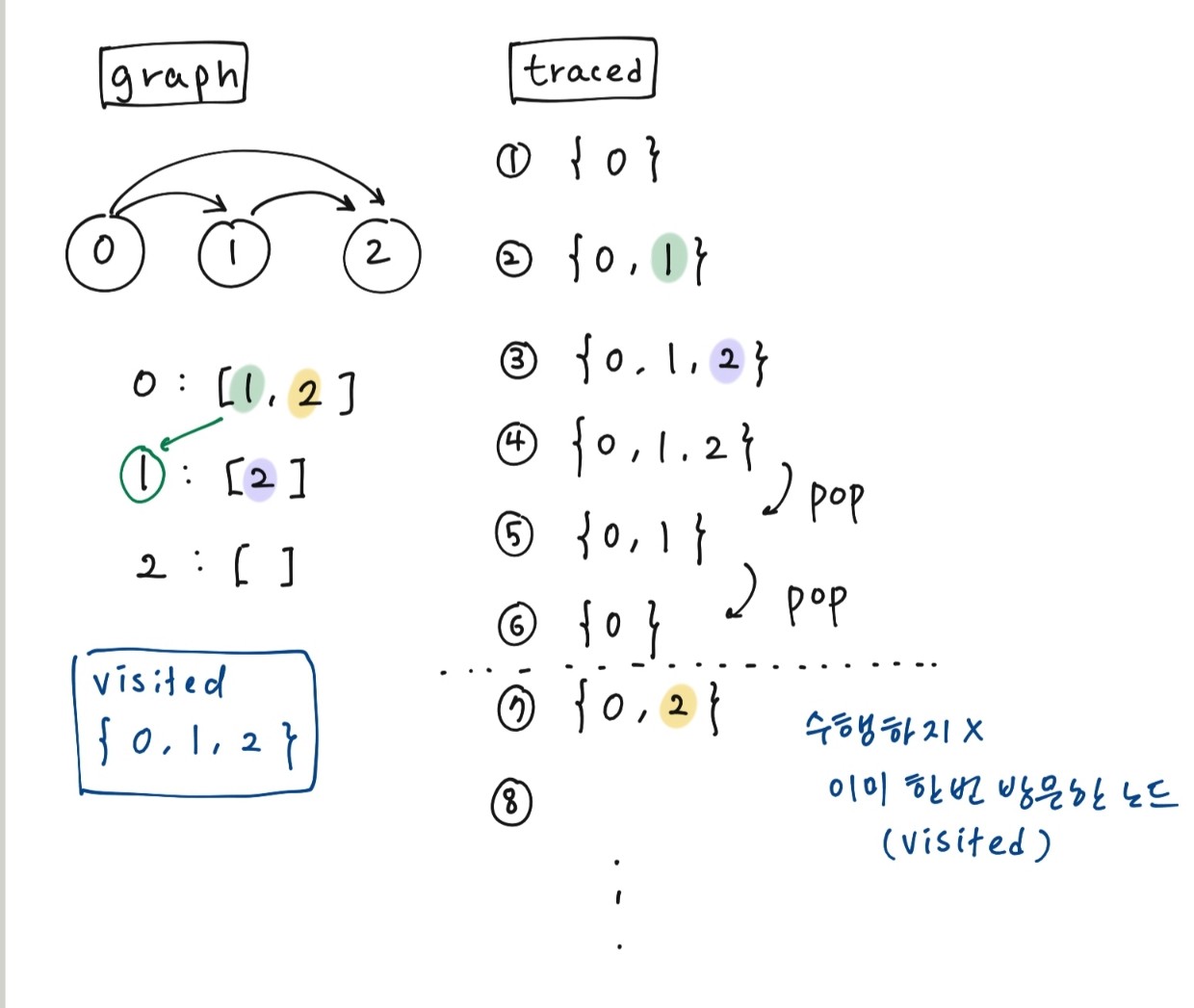
- 사이클이 있는 경우