Facility Locations C++ - 백준 10412

https://acmicpc.net/problem/10412

거의 10개월 정도를 알고 지냈던 문제이다.

에디토리얼을 보고도 이해가 잘 되지 않아

풀다 안풀다 했던 문제이다.

문제 접근

처음에는 $n,m$ 범위가 낮아 백트래킹을 시도해봤지만 당연히 TLE를 맞이했다.

이 문제의 핵심은 $c_{ij}\leq c_{ij'}+c_{i'j}+c_{i'j'}$을 사용하는 것이다.

이 부등식으로 얻을 수 있는 정보는 다음과 같다.

1. location i와 j가 연결된 경우$(c_{ij}=0)$

$0\leq c_{ij'}+c_{i'j}+c_{i'j'}$

이기 때문에 (연결된 경우는 $i-j$로 표현한다.)

1. $i-j',i'-j,i'-j'$
2. $i-j',i'-j$
3. $i-j',i'-j'$
4. $i'-j,i'-j'$
5. $i'-j$
6. $i'-j'$
7. $i-j'$
8. 연결 없음

사실 위 경우는 직관적으로 와닿지 않는다.

그냥 그저 $i-j$일 경우 모든 경우가 가능하구나를 알 수 있다.

2. location i와 j가 연결되지 않은 경우

$0<c_{ij}$이기 때문에

$c_{ij'}$나 $c_{i'j}$, $c_{i'j'}$ 셋 중 하나는 항상 0보다 커야한다.

즉 연결되어있지 않아야한다.

만약 세 개 모두 연결되어 있다면

$i,j$는 무조건 연결되어 있다는 사실을 알 수 있다.

따라서 Location 쌍 $i,i'$ Client 쌍 $j,j'$에 대하여

$i$와 $i'$이 한 connected component(연결 요소)에 속한다면

무조건 Location-Client 부분 이분 그래프는 완전 이분 그래프이다.

예를 들어 다음과 같은 그래프일때 (왼쪽이 Location, 오른쪽이 Client이다.)

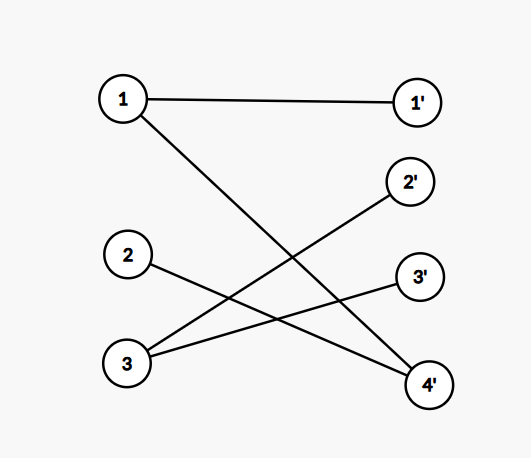
위 부등식에 의해 우리는 당연히 2와 1'이 연결되있다는 사실을 알 수 있고,

위 부등식에 의해 모든 connected component는 complete bipartite graph

인 것을 알 수 있다.

완전 이분 그래프의 $E(V,U)$ 특징은 한 노드 집합 $V$에 대해 $v\in V$

$\forall\;u\in U$ $v$와 $u$가 연결되어 있다는 것이고

이는 하나의 Location에 대해 그 Location connected component에 속한

모든 Client들에게 cost 0으로 서비스를 제공할 수 있다는 뜻이다.

따라서 모든 Client가 서비스를 제공 받고 있으면서

connected component의 개수가 $k$개 이하이면 $n$명의 Client에게

서비스를 제공할 수 있다.

connected component를 관리하기 위해 유니온 파인드 알고리즘을

사용했다.

코드는 다음과 같다.

#include <bits/stdc++.h>
typedef long long ll;
using namespace std;

int parent[200];
int cnt[200];
bool vis[200];

int getParent(int x){
    if(x==parent[x]) return x;
    return parent[x]=getParent(parent[x]);
}

void unionParent(int a, int b){
    a=getParent(a);
    b=getParent(b);
    if(a>b){
        parent[a]=b;
        cnt[b]+=cnt[a];
    }
    else{
        parent[b]=a;
        cnt[a]+=cnt[b];
    }
}

int main(){
    ios_base::sync_with_stdio(false); cin.tie(NULL);
    int m,n,k;
    cin >> m >> n >> k;
    for(int i=0;i<200;i++){
        parent[i]=i;
        cnt[i]=1;
    }
    for(int i=0;i<m;i++){
        for(int j=0;j<n;j++){
            int cost;
            cin >> cost;
            if(cost) continue;
            unionParent(i,j+100);
        }
    }
    int res=0;
    for(int i=0;i<n;i++){
        int p=getParent(i+100);
        if(cnt[p]==1){
            cout << "no";
            return 0;
        }
        if(vis[p]) continue;
        res++;
        vis[p]=1;
    }
    cout << (res>k?"no":"yes");
    return 0;
}