오민식의 고민 C++ - 백준 1219

https://www.acmicpc.net/problem/1219

벨만 포드 문제.

중요한 반례가 발목 잡았던 문제이다.

문제 접근

버스 이용료는 양수로, 벌 수 있는 돈은 음수로 처리해

최단 거리를 구하면 되는 문제이다.

음수 사이클 판별을 위해 벨만 포드 알고리즘을 사용해야 했다.

$N$번째 간선 연결 때 도착 지점이나 시작 지점의 최단 거리가

갱신되면 무조건 음수 사이클이 있다고 생각하고 제출했다.

그리고 틀렸다.

왜냐하면 $N$번째 간선 연결 때 시작 지점, 도착 지점의

최단 거리가 갱신되지 않을 수도 있기 때문이다.

예를 들어 아래 그래프를 보자.

출처 : 백준 게시판

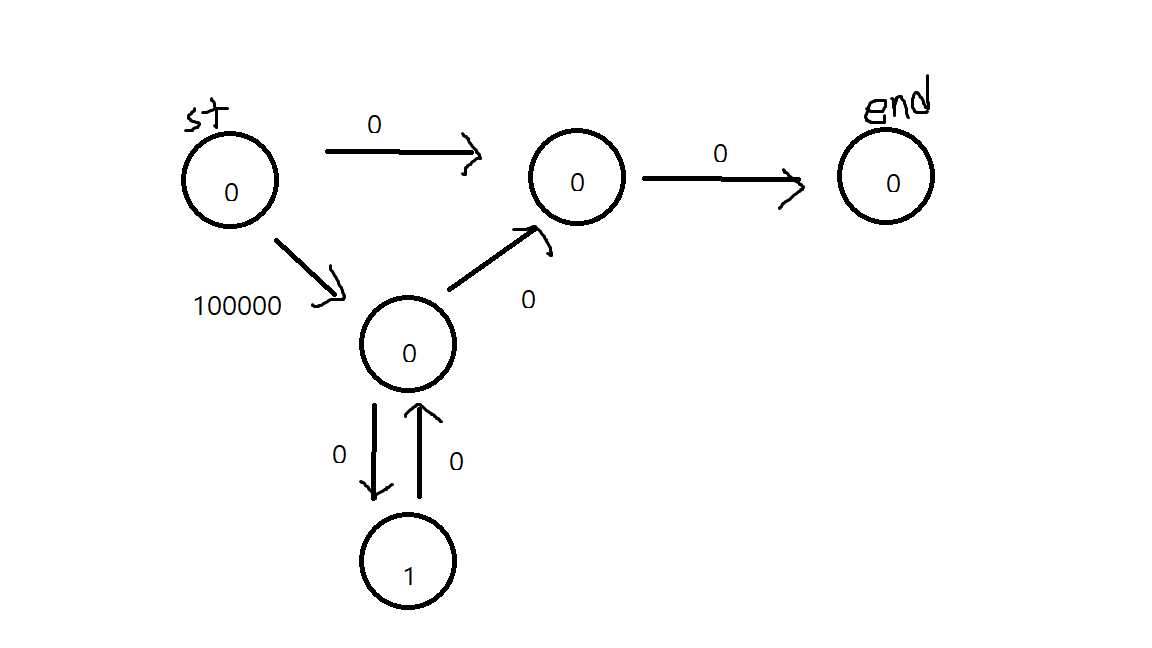
이 경우 가중치가 10만인 간선의 도착 지점에서 음수 사이클이 생기는데

$N=5$이기 때문에 시작 지점이나 도착 지점의 최단 거리 테이블은 갱신되지

않는다. (물론 반복을 간선 가중치+1 만큼 하면 갱신될 것이다.)

이 경우는 도착지점이나 시작지점이 갱신되지 않더라도 어떤 지점에서

최단거리 테이블이 갱신되면 그 곳에서

도착지점으로 갈 수 있는지를 확인해야 된다는 것을 알려주는 반례이다.

이를 종합적으로 구현한 코드는 다음과 같다.

#include <bits/stdc++.h>
#define INF INT32_MAX
#define FI first
#define SE second
typedef long long ll;
using namespace std;

int n,s,e,m;
vector<pair<int,ll>> graph[50];
ll earn[50];
ll d[50];
queue<int> q;
bool vis[50];

int main(){
    ios_base::sync_with_stdio(false); cin.tie(NULL);
    cin >> n >> s >> e >> m;
    fill(d,d+50,INF);
    for(int i=0;i<m;i++){
        int a,b,c;
        cin >> a >> b >> c;
        graph[a].push_back({b,c});
    }
    for(int i=0;i<n;i++) cin >> earn[i];
    d[s]=-earn[s];
    for(int i=0;i<n;i++){
        for(int j=0;j<n;j++){
            for(int k=0;k<graph[j].size();k++){
                int a=j;
                int b=graph[j][k].FI;
                ll c=graph[j][k].SE;
                if(d[a]!=INF && d[a]+c-earn[b]<d[b]){
                    if(i==n-1){
                        q.push(b);
                        vis[b]=1;
                    }
                    d[b]=d[a]+c-earn[b];
                }
            }
        }
    }
    while(!q.empty()){
        int x=q.front();
        q.pop();
        for(int i=0;i<graph[x].size();i++){
            int nx=graph[x][i].FI;
            if(vis[nx]) continue;
            vis[nx]=1;
            q.push(nx);
        }
    }
    if(vis[e]) cout << "Gee";
    else if(d[e]==INF) cout << "gg";
    else cout << -d[e];
    return 0;
}