소수(Prime Number)

• 소수란 1보다 큰 자연수 중에서 1과 자기 자신을 제외한 자연수로는 나누어 떨어지지 않는 자연수

# 소수 판별 함수
def is_prime_number(x):
    # 2부터 (x-1)까지의 모든 수를 확인하며
    for i in range(2,x):
        # x가 해당 수로 나누어 떨어진다면
        if x % i == 0:
            return False # 소수가 아님
    return True # 소수임

print(is_prime_number(4))
print(is_prime_number(7))

소수의 판별: 기본적인 알고리즘 성능 분석

약수의 성질

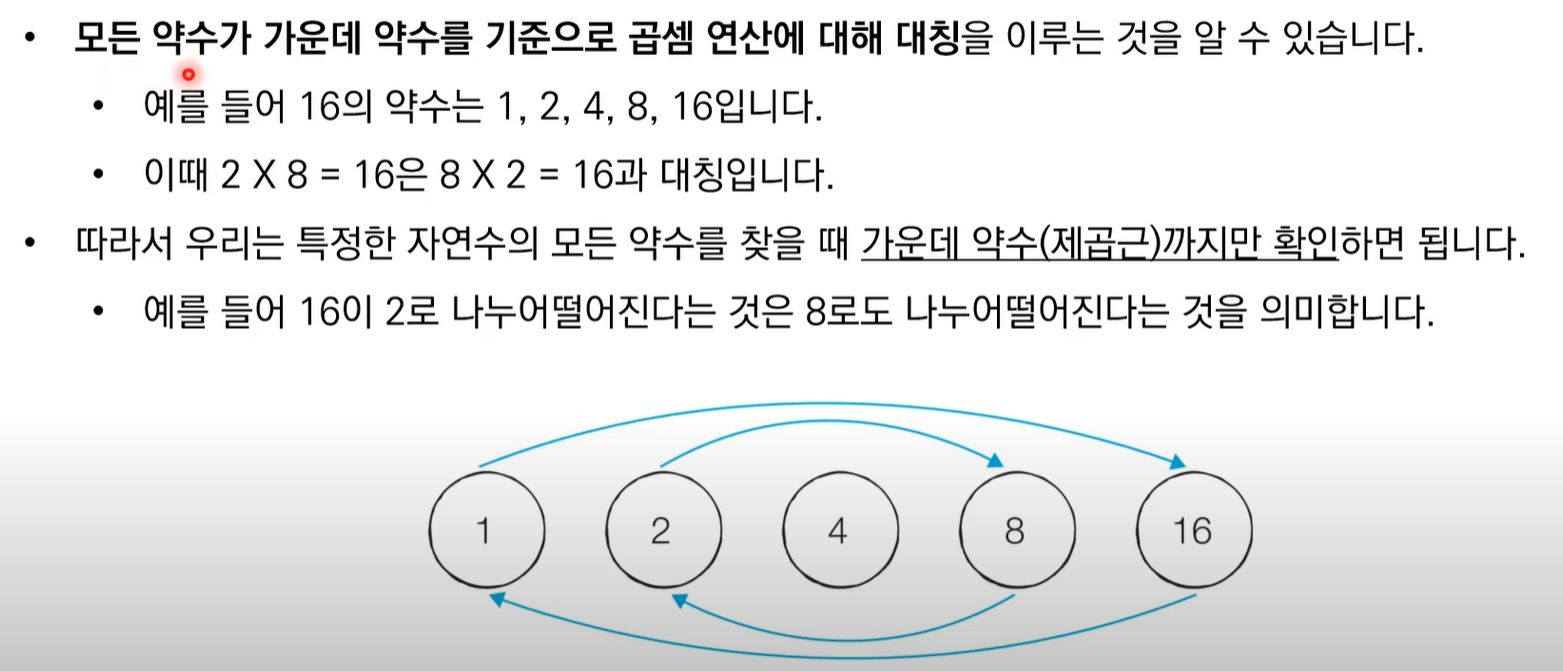
개선된 알고리즘

import math

# 소수 판별 함수
def is_prime_number(x):
    # 2부터 x의 제곱근까지의 모든 수를 확인하며
    for i in range(2,int(math.sqrt(x))+1):
        if x % i == 0:
            return False
    return True

print(is_prime_number(4))
print(is_prime_number(7))

개선된 알고리즘 성능 분석

다수의 소수 판별

에라토스테네스의 체 알고리즘

• 다수의 자연수에 대하여 소수 여부를 판별
• N보다 작거나 같은 모든 소수를 찾을 때 사용 가능
• 구체적인 동작 과정은 다음과 같음

에라토스테네스의 체 알고리즘 동작 예시

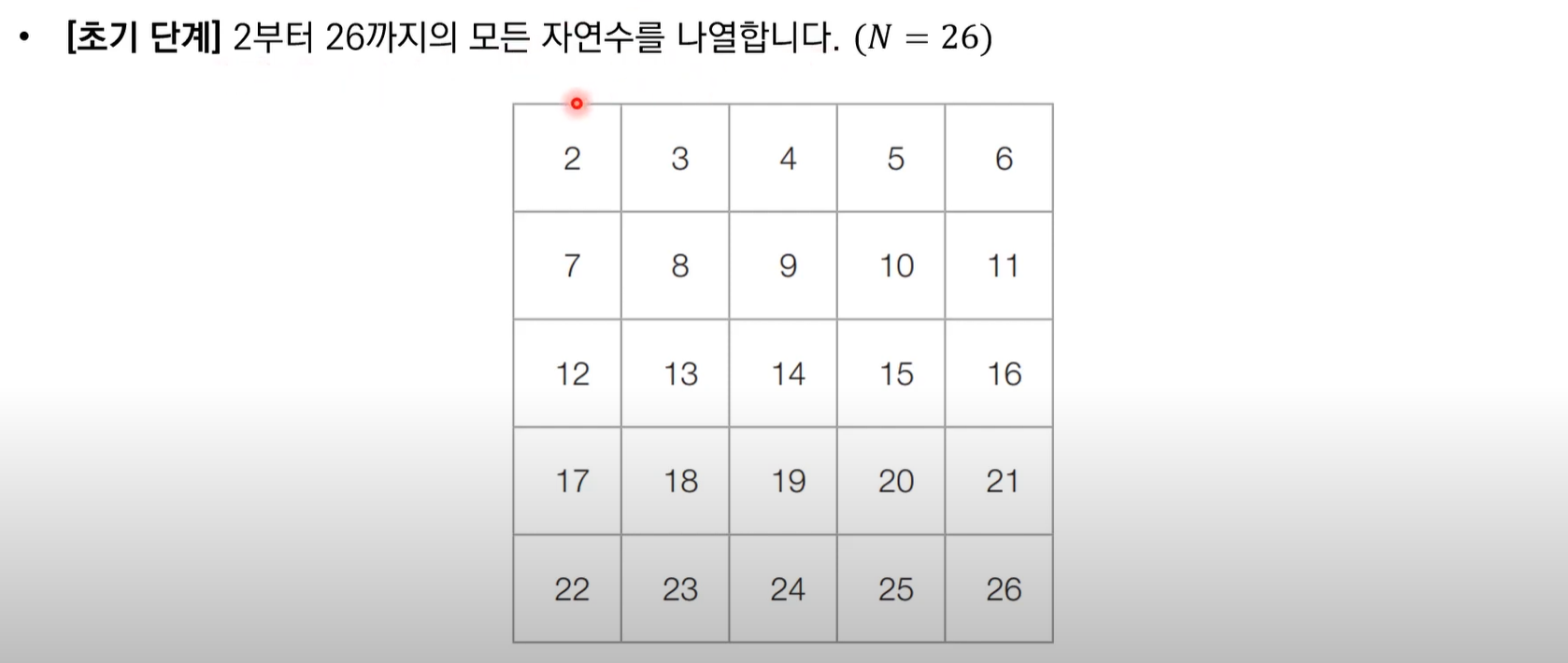
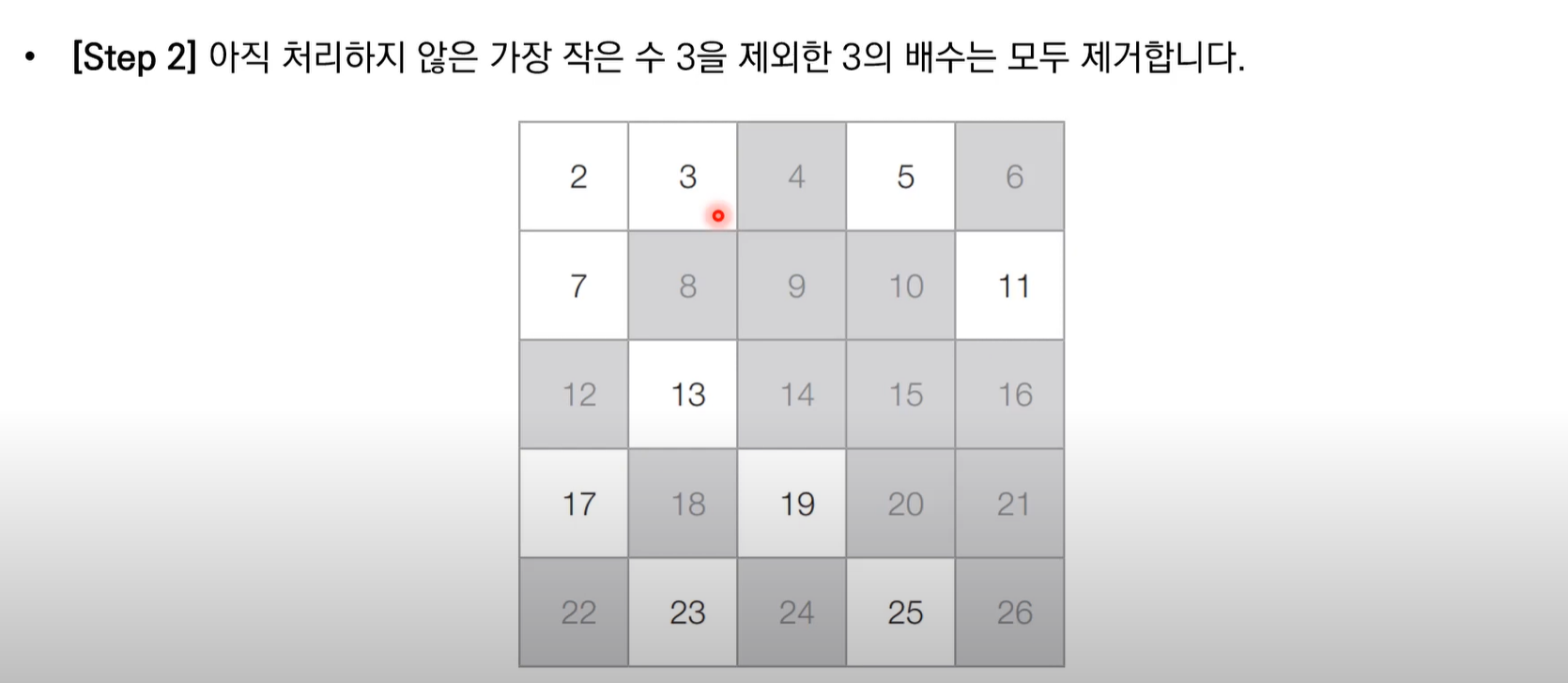
에라토스테네스의 체 알고리즘 구현

import math

n = 1000 # 2부터 1000까지의 모든 수에 대하여 소수 판별
# 처음에 모든 수가 소수(True)인 것으로 초기화(0과 1은 제외)
arr = [True for i in range(n+1)]

# 에라토스테네스의 체 알고리즘 수행
# 2부터 n의 제곱근까지의 모든 수를 확인하며
for i in range(2,int(math.sqrt(n))+1):
    if arr[i] == True: # i가 소수인 경우(남은 수인 경우)
        # i를 제외한 i의 모든 배수를 징기
        j = 2
        while i * j <= n:
            arr[i*j] = False
            j += 1

# 모든 소수 출력
for i in range(2,n+1):
    if arr[i]:
        print(i,end = ' ')

에라토스테네스의 체 알고리즘 성능 분석