Constraint-based Algorithm_basic

Note : Basis of Constraint-based Algorithm

Pseudo Code

[Assumption]

• No hidden confounder Assumption
• Markov Causal Assumption
• Faithfulness Assumption

Problem : Given a set IND of d-separations, determine the DAG pattern faithful
to IND if there is one

Input : a set V of nodes and a set IND of d-separations among subsets of the
nodes

Outputs : If IND admits a faithful DAG representation, the DAG pattern gp
containing the d-separations in this set

def basic(V, IND, Empty Graph G) -> Graph G:
	S[(x,y)] <- A list containing the set Sxy 
							that render X and Y are conditional independent

	for each pair of nodes (X, Y) in V:
		# step 0
		for subset S_ in V/{X, Y}:
			if I({X},{Y}|S_) in IND: 
				S[(X,Y)].append(S_)
		
		if S[(X,Y)] is empty:
			# step 1
			create the link X - Y in G
	
	for each uncoupled meeting X - Z - Y in V:
		# step 2
		if Z not in every S in S[(X, Y)]:
			orient X - Z - Y as X -> Z <- Y
	
	while more edges can be oriented:
		# step 3
		for each uncoupled meeting X -> Z - Y:
			orient Z - Y  as Z -> Y
		# step 4
		for each link X - Y such that there is a path from X to Y:
			orient X - Y as X -> Y
		# step 5
		for each uncoupled meeting X - Z - Y such that X -> W, Y -> W, and Z - W:
			orient Z - W as Z -> W
	
	return G

❗ The original code is C-style, so I modify the code to be similar to Python style

It effectively illustrates the primary framework of Constraint-based algorithms :

Find Skeleton by relation of adjacency and d-separation (step 0 & 1)
→ Find V-structure by lemma 1 (Verma and Pearl, 1991) [4] (step 2)
→ Apply Meek rules [5] (step 3~5)
→ Proof Soundness and Completeness with DAG pattern by the theorem of Meek [5]

Soundness & Completeness of basic algorithm

If the set of d-separations, which are the input to the basic algorithm, admit a faithful DAG representation, the algorithm creates this DAG pattern containing the d-separations in this set. In the other word, every link and directed edge in the DAG pattern created by the basic algorithm is sound and complete with link and directed edge in DAG pattern containing the d-separations in this set.

This fact is important. Because we can indirectly prove the soundness and completeness of our new constraint-based algorithm through this basic algorithm. For example, PC algorithm modifies step 0 & 1 in the basic algorithm to improve efficiency. Also, conservative PC algorithm additionally modifies step 3 in PC algorithm. This is the reason why the name of this algorithm is 'basic'.

Implementation

STEP 0 & 1 : Find Skeleton by relation of adjacency and d-separation ( = p-independence in practice)

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from collections import deque
from itertools import combinations, chain
from collections import defaultdict

# STEP 0
def identify_skeleton_from_empty_graph(self, data, test_kwarg):
    self.ptn = pattern()
    self.ptn.add_vertex(list(data.columns))

    self.p_independence_set = defaultdict(lambda: defaultdict(set))
    
    pairs = combinations(self.ptn.vertex, 2)
    for x, y in pairs:
        v_not_x_y = list(self.ptn.vertex - {x, y})
        power_set_of_v_not_x_y = chain(*[combinations(v_not_x_y, n) for n in range(len(v_not_x_y) + 1)])
        for subset in power_set_of_v_not_x_y:
            if self.test(data, {x}, {y}, set(subset), **test_kwarg):
                self.p_independence_set[x][y]
                self.p_independence_set[y][x] = self.p_independence_set[x][y]
                self.p_independence_set[x][y].add(subset)
                break

    self.identify_skeleton_by_ind(self.p_independence_set)

# STEP 1
def identify_skeleton_by_ind(self, ind, vertex:set = None):
    self.ptn.add_vertex(list(ind.keys()))
    if vertex is not None: self.ptn.add_vertex(vertex)

    self.p_independence_set = ind

    pairs = combinations(self.ptn.vertex, 2)

    for x, y in pairs:
        if len(self.p_independence_set[x][y]) == 0:
            self.ptn.add_link(x, y)

STEP 2 : Find V-structure with adjacency orient faithfulness

def identify_v_structure_with_adjacency_orient_faithfulness(self):
    uncoupled_triple = deque()
    for x in self.ptn.link.keys():
        for z in self.ptn.link[x].keys():
            for y in self.ptn.link[z].keys():
                # Check whether x-z-y is uncoulped meeting
                if x != y and not self.ptn.is_adjacent(x, y): 
                    # Check whether Z not in every S in S[(X, Y)]:
                    if all(z not in subset for subset in self.p_independence_set[x][y]) : uncoupled_triple.append((x, y, z))
    
    while uncoupled_triple:
        x, y, z = uncoupled_triple.popleft()
        #if Z not in every S in S[(X, Y)]:
        # orient X - Z - Y as X -> Z <- Y
        self.ptn.remove_links([(x,z), (y,z)])
        self.ptn.add_edges([(x,z), (y,z)])

STEP 3

def identify_meeks_rule_2(self):
    uncoupled_triple = deque()
    for x in self.ptn.child.keys():
        for z in self.ptn.child[x].keys():
            for y in self.ptn.link[z].keys():
                # Check whether x-z-y is uncoulped meeting
                if x != y and not self.ptn.is_adjacent(x, y): uncoupled_triple.append((x, y, z))

    if len(uncoupled_triple) == 0: return False

    while uncoupled_triple:
        x, y, z = uncoupled_triple.popleft()
        # X -> Z - Y is not v-structure, therefore 
        # orient Z - Y  as Z -> Y
        self.ptn.remove_links([(y,z)])
        self.ptn.add_edges([(z,y)])

    return True

STEP 4

def identify_meeks_rule_3(self):
    pairs = deque()
    for x in self.ptn.link.keys():
        for y in self.ptn.link[x].keys(): 
            # Check there is a path X->Y
            if len(self.ptn.get_path(x, y, directed=True)) > 0: pairs.append((x, y))
    
    if len(pairs) == 0: return False

    while pairs:
        x, y = pairs.popleft()
        #Given graph G is DAG, therefore there is not cyclic path between X and Y
        #However, if Y -> X, then there is cyclic path : X -> ... -> Y -> X
        # thus orient X - Y as X -> Y
        self.ptn.remove_links([(x,y)])
        self.ptn.add_edges([(x,y)])
    
    return True

STEP 5

def identify_meeks_rule_4(self):
    pairs = deque()
    for w in self.ptn.parent.keys():
        # Find W which has more than two parents and at least one vertex linked with
        if len(self.ptn.parent[w].keys()) >= 2 and w in self.ptn.link.keys():
            linked_with_w = set(self.ptn.link[w].keys())

            # Find pair of parents of W (x, y) such that x is not adjacent with y
            # X   Y
            #  \ /
            #   ><
            #   W
            parent_of_w = list(self.ptn.parent[w].keys())
            xy = combinations(parent_of_w, 2)

            for x, y in xy:
                if not self.ptn.is_adjacent(x, y):
                    # Find Z such that X - Z, Y - Z, and W - Z
                    linked_with_x = set(self.ptn.link[x].keys())
                    linked_with_y = set(self.ptn.link[y].keys())
                    linked_with_x_y_w = linked_with_w & linked_with_x & linked_with_y

                    for z in linked_with_x_y_w: pairs.append((z, w))
    
    if len(pairs) == 0: return False
    while pairs:
        z, w = pairs.popleft()
        # Now, we know that 
        # X - Z - Y
        #  \  |  /
        #   > W <
        # X - Z - Y is not v-structure -> Z is parent of X or Y
        # if Z <- W, there is a cyclic path through X or Y 
        # thus orient Z - W as Z -> W

        self.ptn.remove_links([(z,w)])
        self.ptn.add_edges([(z,w)])

    return True

class basic

pip install cdpi --upgrade

Looking in indexes: https://pypi.org/simple, https://us-python.pkg.dev/colab-wheels/public/simple/
Requirement already satisfied: cdpi in /usr/local/lib/python3.9/dist-packages (0.0.9)
Requirement already satisfied: matplotlib in /usr/local/lib/python3.9/dist-packages (from cdpi) (3.7.1)
Requirement already satisfied: pandas in /usr/local/lib/python3.9/dist-packages (from cdpi) (1.4.4)
Requirement already satisfied: scipy in /usr/local/lib/python3.9/dist-packages (from cdpi) (1.10.1)
Requirement already satisfied: numpy in /usr/local/lib/python3.9/dist-packages (from cdpi) (1.22.4)
Requirement already satisfied: contourpy>=1.0.1 in /usr/local/lib/python3.9/dist-packages (from matplotlib->cdpi) (1.0.7)
Requirement already satisfied: pyparsing>=2.3.1 in /usr/local/lib/python3.9/dist-packages (from matplotlib->cdpi) (3.0.9)
Requirement already satisfied: importlib-resources>=3.2.0 in /usr/local/lib/python3.9/dist-packages (from matplotlib->cdpi) (5.12.0)
Requirement already satisfied: cycler>=0.10 in /usr/local/lib/python3.9/dist-packages (from matplotlib->cdpi) (0.11.0)
Requirement already satisfied: fonttools>=4.22.0 in /usr/local/lib/python3.9/dist-packages (from matplotlib->cdpi) (4.39.2)
Requirement already satisfied: kiwisolver>=1.0.1 in /usr/local/lib/python3.9/dist-packages (from matplotlib->cdpi) (1.4.4)
Requirement already satisfied: pillow>=6.2.0 in /usr/local/lib/python3.9/dist-packages (from matplotlib->cdpi) (8.4.0)
Requirement already satisfied: python-dateutil>=2.7 in /usr/local/lib/python3.9/dist-packages (from matplotlib->cdpi) (2.8.2)
Requirement already satisfied: packaging>=20.0 in /usr/local/lib/python3.9/dist-packages (from matplotlib->cdpi) (23.0)
Requirement already satisfied: pytz>=2020.1 in /usr/local/lib/python3.9/dist-packages (from pandas->cdpi) (2022.7.1)
Requirement already satisfied: zipp>=3.1.0 in /usr/local/lib/python3.9/dist-packages (from importlib-resources>=3.2.0->matplotlib->cdpi) (3.15.0)
Requirement already satisfied: six>=1.5 in /usr/local/lib/python3.9/dist-packages (from python-dateutil>=2.7->matplotlib->cdpi) (1.16.0)

from cdpi import pattern
from cdpi.causal_discovery.test import get_test

class basic:
    def __init__(self):
        self.ptn = pattern()
    
    def identify(self, data:pd.DataFrame = None, test:str = None, ind:dict = None, vertex = None, **test_kwarg) -> pattern: 
        # STEP 0 ~ 1 : Find skeleton
        if ind is not None:
            self.identify_skeleton_by_ind(ind, vertex)
        elif data is not None and test is not None:
            self.test = get_test(test)
            self.identify_skeleton_from_empty_graph(data, test_kwarg = test_kwarg)
        else:
            print("basic.identify : both ind and (data, test) are None!")

        # # STEP 2 : Find v-structure
        self.identify_v_structure_with_adjacency_orient_faithfulness()

        # STEP 3~5 : use Meek rules
        cnt = True
        while cnt:
          cnt2 = self.identify_meeks_rule_2()
          cnt3 = self.identify_meeks_rule_3()
          cnt4 = self.identify_meeks_rule_4()

          cnt = cnt2 or cnt3 or cnt4 # Check there are vertexs which could be changed

        return self.ptn

    def draw(self):
        self.ptn.draw()

    def draw_by_pos(self, pos):
        self.ptn.draw_by_pos(pos)
        
basic.identify_skeleton_from_empty_graph = identify_skeleton_from_empty_graph
basic.identify_v_structure_with_adjacency_orient_faithfulness = identify_v_structure_with_adjacency_orient_faithfulness
basic.identify_meeks_rule_2 = identify_meeks_rule_2
basic.identify_meeks_rule_3 = identify_meeks_rule_3
basic.identify_meeks_rule_4 = identify_meeks_rule_4
basic.identify_skeleton_by_ind = identify_skeleton_by_ind

Example

np.random.seed(seed=2022)

import scipy.stats as stats

size = 100

data = pd.DataFrame()
data['A'] =  stats.bernoulli(p = 0.5).rvs(size = size)
data['B'] =  stats.bernoulli(p = 0.5).rvs(size = size)
data['C'] =  stats.bernoulli(p = 0.5).rvs(size = size)
data['D'] =  data['A'] + data['B'] + data['C'] + stats.bernoulli(p = 0.5).rvs(size = size)
data['E'] =  data['A'] + data['B'] + stats.bernoulli(p = 0.5).rvs(size = size)

bsc = basic()
bsc.identify(data = data, test = 'conditional_mutual_information_test')
bsc.draw()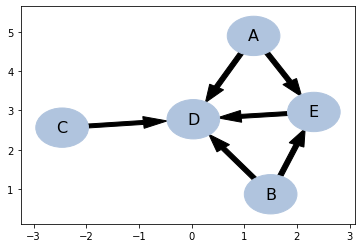

For given IND

ptn = pattern()
ptn.add_edges([
    ('A', 'D'),
    ('D', 'B'),
    ('B', 'E'),
    ('C', 'E'),
    ('C', 'F'),
    ('D', 'H'),
    ('E', 'I'),
    ('F', 'J'),
    ('H', 'K'),
    ('I', 'L'),
    ('J', 'L'),
    ('G', 'J'),
    ('K', 'M')
])
ptn.draw()
pos = ptn.pos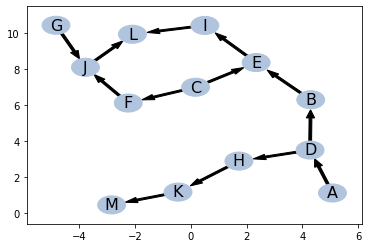

ind = ptn.get_all_d_separation()

bsc = basic()
bsc.identify(ind = ind)

bsc.ptn.draw_by_pos(pos)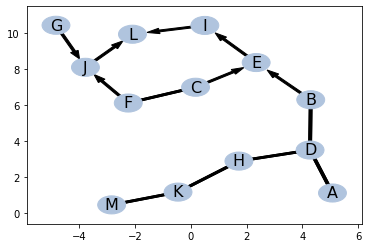

Reference

[3] Metropolitan. (2004). Learning Bayesian Networks. chapter 10.

[4] Verma, T., Pearl, J. (1990). On the Equivalence of Causal Models. Appears in Proceedings of the Sixth Conference on Uncertainty in Artificial Intelligence (UAI1990).

[5] Meek, C. (1995). Causal inference and causal explanation with background
knowledge. Conference on Uncertainty in Artificial Intelligence.