Constraint-based Algorithm_cpc

Note : Conservative PC Algorithm

Pseudo Code

[Assumption]

• No hidden confounder Assumption
• Markov Causal Assumption
• Adjacency-Faithfulness Assumption❗
  [6]

❓ What is 'Basic algorithm'? ⇒ See Constraint-based Algorithm_basic

Adjacency-Faithfulness and Orientation-Faithfulness

As you can see in the implementation of Basic algorithm and PC algorithm, p-independence information, IND, is used only to configure skeleton and to find v-structure in step 1 and 2. The remaining steps rely solely on the definition of the DAG and the fact that a given uncoupled triple is not a v-structure.

In this context, the faithfulness assumption can be seen as consisting of two distinct assumptions : one related to the construction of the skeleton and the other related to the identification of v-structure. Let call the former Adjacency-Faithfulness, because it is related to adjacency between vertexes :

Adjacency-Faithfulness
if $X$ and $Y$ are adjacent in DAG G, then $X$ and $Y$ are dependent conditional on any subset of $V/\{X, Y\}$

And let call the latter Orientation-Faithfulness, because it is related to orientation of uncoupled triple :

Orientation-Faithfulness
Let (X, Y, Z) be any uncoupled triple in DAG G.
(1) if $X$ → $Z$ ← $Y$, then $X$ and $Y$ are dependent given any subset of $V\{X,Y\}$ that contains $Z$.
(2) Otherwise, $X$ and $Y$ are dependent conditional on any subset of $V\{X,Y\}$ that does not contains $Z$.

The Basic and PC algorithms assume both of these faithfulness. However, these two assumptions do not always hold, and even if Adjacency-Faithfulness holds, Orientation-Faithfulness may not holds. For example, consider the following cases.

$G:X\rightarrow Y→ Z \\IND : X \perp_pZ\ \&\ X\perp_pZ|Y$

In this case, Adjacency-Faithfulness holds, but Orientation-Faithfulness is not satisfied, because Y is not only included in some conditions that render X and Z are conditional independent and but also excluded in other conditions. Therefore, the skeleton of (X, Y, Z) can be indentified, but the orientation is not determined.

The problem is that Basic algorithm and PC algorithm only check $X \perp_pZ$ and do not further check the conditonal independence between X and Z. So they orient the triple X-Y-Z as X → Y ← Z. In order to prevent error when Orientation-Faithfulness is not satisfied, (orientation) unfaithful triple must be dealt with separately. It is the main idea of Conservative PC Algorithm. [6]

Soundness & Completeness of Conservative PC algorithm

If both faithfulness assumption holds, Conservative PC algorithm is same with PC algorithm. Therefore the result is sound and complete.

If Orientation-Faithfulness is not satisfied, the link in the result is sound and complete but the edge is only sound.

Implementation

❗ We do not need to change step 4, because it uses only the definition of DAG.

❗ In step 1, We only need to delete the code break

❗ In step 3 and 5, We only need to add the code if (x,z,y) in self.unfaithful_triple : continue

STEP 0 & 1 : Find Skeleton by relation of adjacency and d-separation ( = p-independence in practice)

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from collections import deque
from itertools import combinations, chain
from collections import defaultdict

def identify_skeleton_from_full_link_graph_in_cpc(self, data, test_kwarg):
    self.ptn = pattern()
    self.ptn.add_vertex(list(data.columns))

    self.p_independence_set = defaultdict(set)
    self.p_independence_set = defaultdict(lambda: defaultdict(set))
    self.ptn.full_link()

    adj = {x : self.ptn.adjacent(x) for x in self.ptn.vertex}
    
    i = 0
    while any(i < len(adj[x]) for x in adj.keys()):
        for x in self.ptn.vertex:
            adj_x = adj[x]

            for y in adj_x:
                adj_x_not_y = list(adj_x - {y})
                power_set = combinations(adj_x_not_y, i)
                for subset in power_set:
                    if self.test(data, {x}, {y}, set(subset), **test_kwarg):
                        self.p_independence_set[x][y]
                        self.p_independence_set[y][x] = self.p_independence_set[x][y]
                        self.p_independence_set[x][y].add(subset)

                        self.ptn.remove_links([(x, y)])
                        # Do NOT break
            
            adj[x] = self.ptn.adjacent(x)

        i += 1

STEP 2 : Find V-structure with checking Orientation-faithfulness

def identify_v_structure_with_adjacency_faithfulness(self):
    uncoupled_triple = deque()
    self.unfaithful_triple = set()

    for x in self.ptn.link.keys():
        for z in self.ptn.link[x].keys():
            for y in self.ptn.link[z].keys():
                if x != y and not self.ptn.is_adjacent(x, y): 
                    # Check Orientation-faithfulness
                    if all(z not in subset for subset in self.p_independence_set[x][y]) : uncoupled_triple.append((x, y, z))
                    elif all(z in subset for subset in self.p_independence_set[x][y]) : continue
                    
                    # If Orientation-faithfulness is not satisfied, 
                    # label the triple as 'unfaithful' triple
                    else: self.unfaithful_triple.add((x,z,y))
                    
    while uncoupled_triple:
        x, y, z = uncoupled_triple.popleft()
        self.ptn.remove_links([(x,z), (y,z)])
        self.ptn.add_edges([(x,z), (y,z)])

STEP 3

def identify_meeks_rule_2_in_cpc(self):
    uncoupled_triple = deque()
    for x in self.ptn.child.keys():
        for z in self.ptn.child[x].keys():
            for y in self.ptn.link[z].keys():
                # Check whether the triple x->z-y is unfaithful or not
                # If unfaithful, pass
                if (x,z,y) in self.unfaithful_triple : continue
                if x != y and not self.ptn.is_adjacent(x, y): uncoupled_triple.append((x, y, z))

    if len(uncoupled_triple) == 0: return False

    while uncoupled_triple:
        x, y, z = uncoupled_triple.popleft()
        self.ptn.remove_links([(y,z)])
        self.ptn.add_edges([(z,y)])

    return True

STEP 5

def identify_meeks_rule_4_in_cpc(self):
    pairs = deque()
    for w in self.ptn.parent.keys():
        if len(self.ptn.parent[w].keys()) >= 2 and w in self.ptn.link.keys():
            linked_with_w = set(self.ptn.link[w].keys())
            parent_of_w = list(self.ptn.parent[w].keys())
            xy = combinations(parent_of_w, 2)

            for x, y in xy:
                if not self.ptn.is_adjacent(x, y):
                    linked_with_x = set(self.ptn.link[x].keys())
                    linked_with_y = set(self.ptn.link[y].keys())
                    linked_with_x_y_w = linked_with_w & linked_with_x & linked_with_y
                    
                    for z in linked_with_x_y_w: 
                        # Check whether the triple x-z-y is unfaithful or not
                        # If unfaithful, pass
                        if (x,z,y) in self.unfaithful_triple : continue
                        pairs.append((z, w))
    
    if len(pairs) == 0: return False
    while pairs:
        z, w = pairs.popleft()
        self.ptn.remove_links([(z,w)])
        self.ptn.add_edges([(z,w)])

    return True

class cpc

pip install cdpi -q

from cdpi import pattern
from cdpi.causal_discovery.test import get_test
from cdpi.causal_discovery.util import (identify_skeleton_by_ind,
                                        identify_meeks_rule_3)

class cpc:
    def __init__(self):
        self.ptn = pattern()
    
    def identify(self, data:pd.DataFrame = None, test:str = None, ind:dict = None, vertex = None, **test_kwarg) -> pattern: 
        # STEP 0 ~ 1 : Find skeleton
        if ind is not None:
            self.identify_skeleton_by_ind(ind, vertex)
        elif data is not None and test is not None:
            self.test = get_test(test)
            self.identify_skeleton_from_full_link_graph_in_cpc(data, test_kwarg = test_kwarg)
        else:
            print("cpc.identify : both ind and (data, test) are None!")


        # # STEP 2 : Find v-structure and unfaithful triple
        self.identify_v_structure_with_adjacency_faithfulness()

        # STEP 3~5 : use Meek's rules
        cnt = True
        while cnt:
            cnt2 = self.identify_meeks_rule_2_in_cpc()
            # STEP 3 is not related with orient faithfulness assumption.
            # Because it uses only the definition of DAG
            cnt3 = self.identify_meeks_rule_3() 
            cnt4 = self.identify_meeks_rule_4_in_cpc()

            cnt = cnt2 or cnt3 or cnt4 # Check there are vertexs which could be changed

        return self.ptn
    
    def draw(self):
        self.ptn.draw()
        pos = self.ptn.pos
        self.draw_unfaithful_triple(pos)
    
    def draw_by_pos(self, pos):
        self.ptn.draw_by_pos(pos)
        self.draw_unfaithful_triple(pos)

    # Draw unfaithful triple
    def draw_unfaithful_triple(self, pos):
        for triple in self.unfaithful_triple:
            x, z, y = triple
            
            delta = pos[x] - pos[y]
            l = np.linalg.norm(delta) * 30 / 100
            unit = delta/np.linalg.norm(delta)

            cent = (pos[x] + pos[y]) / 2
            cent = 3 * pos[z]/4 + cent/4
            x, y = cent - unit * l / 2
            dx, dy = unit * l
            plt.arrow(x, y, dx, dy, width = 0.05, color = 'gray', linestyle = '-.')


cpc.identify_skeleton_from_full_link_graph_in_cpc = identify_skeleton_from_full_link_graph_in_cpc
cpc.identify_v_structure_with_adjacency_faithfulness = identify_v_structure_with_adjacency_faithfulness
cpc.identify_meeks_rule_2_in_cpc = identify_meeks_rule_2_in_cpc
cpc.identify_meeks_rule_3 = identify_meeks_rule_3
cpc.identify_meeks_rule_4_in_cpc = identify_meeks_rule_4_in_cpc
cpc.identify_skeleton_by_ind = identify_skeleton_by_ind

Example

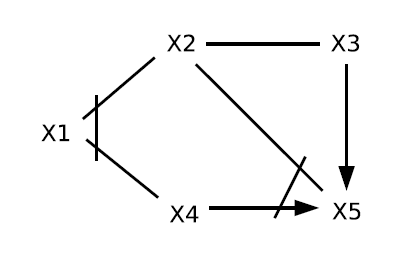[6]

Generating the independence set which satisfies only Adjacency-Faithfulness

ptn = pattern()
ptn.add_edges([
    ('X2', 'X1'),
    ('X4', 'X1'),
    ('X4', 'X5'),
    ('X2', 'X5'),
    ('X4', 'X5'),
    ('X3', 'X2'),
    ('X3', 'X5')
])
pos = {
    'X1' : np.array([0, 2]),
    'X2' : np.array([2, 4]),
    'X4' : np.array([2, 0]),
    'X3' : np.array([4, 4]),
    'X5' : np.array([4, 0])
}
ptn.draw_by_pos(pos)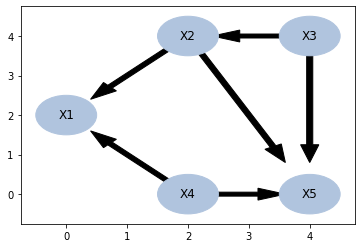

ds = ptn.get_all_d_separation()

ds['X2']['X4'].add(tuple(['X1']))
ds['X2']['X4'].add(tuple(['X5']))
ds['X2']['X4']

{(), ('X1',), ('X3',), ('X5',)}

CPC

cpc_al = cpc()
cpc_al.identify(ind = ds)

<cdpi._pattern.pattern at 0x7f5ef3edb9d0>

cpc_al.unfaithful_triple

{('X2', 'X1', 'X4'),
 ('X2', 'X5', 'X4'),
 ('X4', 'X1', 'X2'),
 ('X4', 'X5', 'X2')}

cpc_al.draw_by_pos(pos)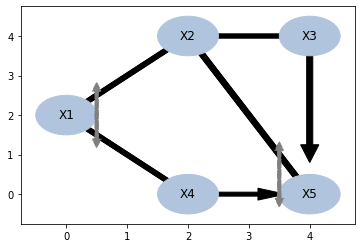

Reference

[6] Ramsey, J., Spirtes, P., & Zhang, J. (2006). Adjacency-faithfulness and conservative causal inference. Proceedings of the 22nd Conference on Uncertainty in Artificial Intelligence, UAI 2006.