DAG Pattern_d_separation

class pattern

Methods related with d-separation

get_d_separation

Return

• a set of every vertex v such that v and X are d-separated by Z. (i.e. $\{v: \newcommand{\indep}{\perp \!\!\! \perp} v\indep_{D} X\ |\ Z,\ v\in V \}$)

The algorithm for finding the d-segmentation set is as follows. [1]

pip install cdpi 

Looking in indexes: https://pypi.org/simple, https://us-python.pkg.dev/colab-wheels/public/simple/
Collecting cdpi
  Downloading cdpi-0.1.0-py3-none-any.whl (14 kB)
Requirement already satisfied: pandas in /usr/local/lib/python3.9/dist-packages (from cdpi) (1.4.4)
Requirement already satisfied: matplotlib in /usr/local/lib/python3.9/dist-packages (from cdpi) (3.7.1)
Requirement already satisfied: scipy in /usr/local/lib/python3.9/dist-packages (from cdpi) (1.10.1)
Requirement already satisfied: numpy in /usr/local/lib/python3.9/dist-packages (from cdpi) (1.22.4)
Requirement already satisfied: packaging>=20.0 in /usr/local/lib/python3.9/dist-packages (from matplotlib->cdpi) (23.0)
Requirement already satisfied: pillow>=6.2.0 in /usr/local/lib/python3.9/dist-packages (from matplotlib->cdpi) (8.4.0)
Requirement already satisfied: python-dateutil>=2.7 in /usr/local/lib/python3.9/dist-packages (from matplotlib->cdpi) (2.8.2)
Requirement already satisfied: pyparsing>=2.3.1 in /usr/local/lib/python3.9/dist-packages (from matplotlib->cdpi) (3.0.9)
Requirement already satisfied: fonttools>=4.22.0 in /usr/local/lib/python3.9/dist-packages (from matplotlib->cdpi) (4.39.2)
Requirement already satisfied: cycler>=0.10 in /usr/local/lib/python3.9/dist-packages (from matplotlib->cdpi) (0.11.0)
Requirement already satisfied: importlib-resources>=3.2.0 in /usr/local/lib/python3.9/dist-packages (from matplotlib->cdpi) (5.12.0)
Requirement already satisfied: contourpy>=1.0.1 in /usr/local/lib/python3.9/dist-packages (from matplotlib->cdpi) (1.0.7)
Requirement already satisfied: kiwisolver>=1.0.1 in /usr/local/lib/python3.9/dist-packages (from matplotlib->cdpi) (1.4.4)
Requirement already satisfied: pytz>=2020.1 in /usr/local/lib/python3.9/dist-packages (from pandas->cdpi) (2022.7.1)
Requirement already satisfied: zipp>=3.1.0 in /usr/local/lib/python3.9/dist-packages (from importlib-resources>=3.2.0->matplotlib->cdpi) (3.15.0)
Requirement already satisfied: six>=1.5 in /usr/local/lib/python3.9/dist-packages (from python-dateutil>=2.7->matplotlib->cdpi) (1.16.0)
Installing collected packages: cdpi
Successfully installed cdpi-0.1.0

from cdpi import pattern

from collections import deque
from itertools import combinations, chain
from collections import defaultdict

def get_d_separation(self, X, Z) -> set:
    # Test X and Z are disjoint
    if X & Z:
        print('get_d_separation : given two vertex sets are not disjoint!')
        return

    # 1) make descendent list 
    descendent = {v:0 for v in self.vertex}
    for i in self.vertex:
        descendent_of_i = self.get_descendant(i)
        if descendent_of_i&Z or i in Z:
            descendent[i] = 1
    
    # 2) make undirected version of this DAG
    sym_graph = {v: [] for v in self.vertex}
    for pa in list(self.child.keys()) + list(self.link.keys()):
        for ch in self.child[pa].keys():
            sym_graph[pa].append([ch, 0]) # [vertex, label]
            sym_graph[ch].append([pa, 0])

        for ch in self.link[pa].keys():
            sym_graph[pa].append([ch, 0])
    
    # 3) for each x in X, find vertex v such that v and x are d-separated by Z 
    # ez explanation  1) do BFS from 's' in undirected graph we create above
    #                 2) whenever you meet another vertex v in V/X, 
    #                    check the trail 'previous-current-v' is 'active' or not
    #                 3) If the trail is active, v and x are not d-separated by Z.
    #                    Save this fact and append edges v ->its neiborhood to queue
    #                 4) If the trail is not active, stop searching along the trail
    reachable = set()
    queue = deque()
    for v in X:
        queue.append(('', v))
    
    while queue:
        #v1 -> v2
        v1, v2 = queue.popleft()

        for i, v3 in enumerate(sym_graph[v2]):
            v3, label = v3
            if not label and v1 != v3:
                # test whether the trail 'v1-v2-v3' is active
                # first, check : given triple (v1, v2, v3) are v-structure & descendent[v2] = 1
                if v1 in self.parent[v2].keys() and v3 in self.parent[v2].keys(): 
                    if descendent[v2]:
                        reachable.add(v3)
                        sym_graph[v2][i][1] = 1 # labeling
                        queue.append((v2, v3))

                # second, check : given triple (v1, v2, v3) are NOT v-structure & v2 NOT in Z
                elif v2 not in Z:
                    reachable.add(v3)
                    sym_graph[v2][i][1] = 1 # labeling
                    queue.append((v2, v3))

    Ys = self.vertex - (reachable|X|Z)

    return (X, Ys, Z)

pattern.get_d_separation = get_d_separation

d_separated

Return

• True if $\newcommand{\indep}{\perp \!\!\! \perp} X\indep_{D} Y\ |\ Z$, else False

def d_separated(self, X, Y, Z) -> bool:
    # Warning : This method is terribly inefficient
    return Y <= self.get_d_separation(X, Z)[1]

pattern.d_separated = d_separated

add_d_separation

Parameter

• dseparation_set : the set of (X, Y, Z) such that $I{D}(X,Y,Z)$. (ex : { ({ 'A' }, { 'B' }, { 'C' }), ...)

def add_d_separations(self, d_separation_set):
    for ds in d_separation_set:
        x, y, z = ds
        x, y= x.pop(), y.pop()
        z = tuple(z)

        self.d_separation_set[x][y]
        self.d_separation_set[y][x] = self.d_separation_set[x][y]
        self.d_separation_set[x][y].add(z)

pattern.add_d_separations = add_d_separations

get_all_d_separation

Return

• all d-separation in the DAG pattern

def get_all_d_separation(self) -> dict:
    pairs = combinations(self.vertex, 2)
    for x, _ in pairs:
        v_not_x_and_some_v = list(self.vertex - {x, _})
        power_set = chain(*[combinations(v_not_x_and_some_v, n) for n in range(len(v_not_x_and_some_v) + 1)])

        for z in power_set:
            z = set(z)
            ys = self.get_d_separation({x}, z)[1]
            if len(ys) > 0:
                for y in ys:
                    self.add_d_separations([({x}, {y}, z)])

    return self.d_separation_set.copy()

pattern.get_all_d_separation = get_all_d_separation

Example

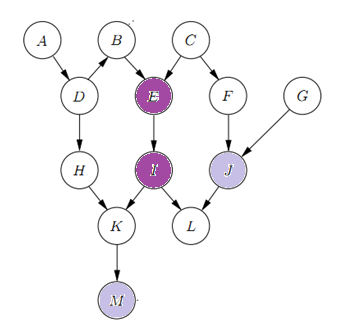
ptn = pattern()
ptn.add_edges([
    ('A', 'D'),
    ('D', 'B'),
    ('B', 'E'),
    ('C', 'E'),
    ('C', 'F'),
    ('D', 'H'),
    ('E', 'I'),
    ('F', 'J'),
    ('H', 'K'),
    ('I', 'K'),
    ('I', 'L'),
    ('J', 'L'),
    ('G', 'J'),
    ('K', 'M')
])

ptn.get_d_separation({'M'}, {'E', 'I'})

({'M'}, {'G'}, {'E', 'I'})

ptn.d_separated({'M'}, {'J'}, {'E', 'I'})

False

ptn = pattern()
ptn.add_edges([
    ('B', 'A'),
    ('C', 'A'),
    ('B', 'D'),
    ('C', 'D'),
    ('D', 'E')
])

ptn.get_all_d_separation()

defaultdict(<function cdpi._pattern.pattern.__init__.<locals>.<lambda>()>,
            {'E': defaultdict(set,
                         {'A': {('B', 'D'), ('C', 'B'), ('C', 'D'), ('D',)},
                          'C': {('B', 'D'), ('D',), ('D', 'A')},
                          'B': {('C', 'D'), ('D',), ('D', 'A')}}),
             'A': defaultdict(set,
                         {'E': {('B', 'D'), ('C', 'B'), ('C', 'D'), ('D',)},
                          'D': {('C', 'B')}}),
             'C': defaultdict(set,
                         {'E': {('B', 'D'), ('D',), ('D', 'A')}, 'B': {()}}),
             'B': defaultdict(set,
                         {'E': {('C', 'D'), ('D',), ('D', 'A')}, 'C': {()}}),
             'D': defaultdict(set, {'A': {('C', 'B')}})})

Reference

[1] Geiger, D., Verma, T., & Pearl, J. (1990). d-Separation: From Theorems to Algorithms. In Machine Intelligence and Pattern Recognition (Vol. 10, Issue C)