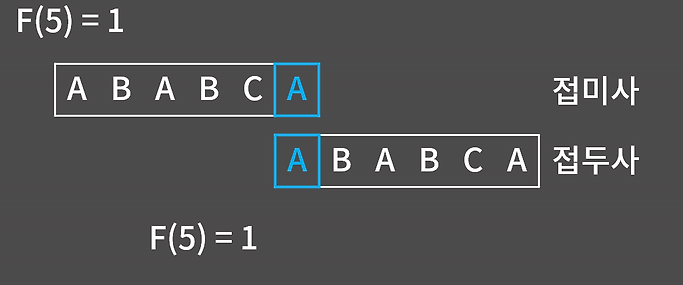KMP

KMP란?

KMP(Knuth-Morris-Pratt)는 문자열이 주어졌을 때 문자열 안에서 어떠한 패턴을 효율적으로 찾는 알고리즘으로 쉽게 말하면 문자열 탐색 알고리즘이다.

일반적으로 문자열 A에서 문자열 B를 찾기 위해서는 A의 처음부터 B의 길이만큼 일일이 비교하게 되어 시간 복잡도는 O(|A||B|)가 된다. 하지만 KMP 알고리즘을 사용하면 O(|A| + |B|) 로 줄일 수 있다.

실패 함수

KMP의 핵심은 바로 실패 함수(Failure Function)이다.
그러면 실패 함수란 무엇인가? 이 함수는 패턴 문자열의 각 위치에서 자기 자신을 제외한 접두사와 접미사가 일치하는 최대 길이를 저장합니다.

F(2)에서 보면

• 접두사: A, AB, ABA
• 접미사: A, BA, ABA
  이 중 자기 자신을 제외하고 접두사와 접미사가 일치하는 경우는 A이므로 F(2) = 1

위의 경우에선 F(5)의 값은 몇인지 확인해 보면 다음과 같다.

• 접미사 ABCA 와 접두사 ABAB -> 다름 F(5) != 4
• 접미사 BCA와 접두사 ABA -> 다름 F(5) != 3
• 접미사 CA와 접두사 AB -> 다름 F(5) != 2
• 접미사 A와 접두사 A -> 같음 F(5) = 1

이런 식으로 구하게 된다면 두 문자열을 비교해야 하니 O(|S|^2)과 F가 0부터 |S|까지의 길이를 다 이렇게 연산하므로 총 O(|S|^3)만큼의 시간 복잡도가 나온다.

그러나 KMP는 아까 말했듯 이러한 문자열 탐색의 비용을 확 줄인 알고리즘으로 이 실패 함수도 O(|S|^3)가 아닌 O(|S|)만큼의 시간 복잡도로 줄일 수 있다.

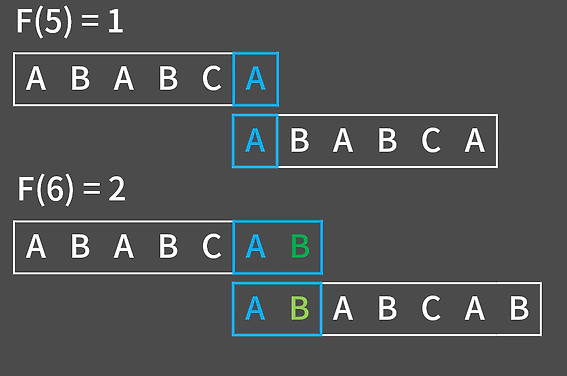
F(6)을 구할 때 어떻게 해야 할지를 생각해 보자. 먼저 시간 복잡도가 저만큼 줄어든다는 것은 DP처럼 값을 저장해가는 방식임을 유추할 수 있다.

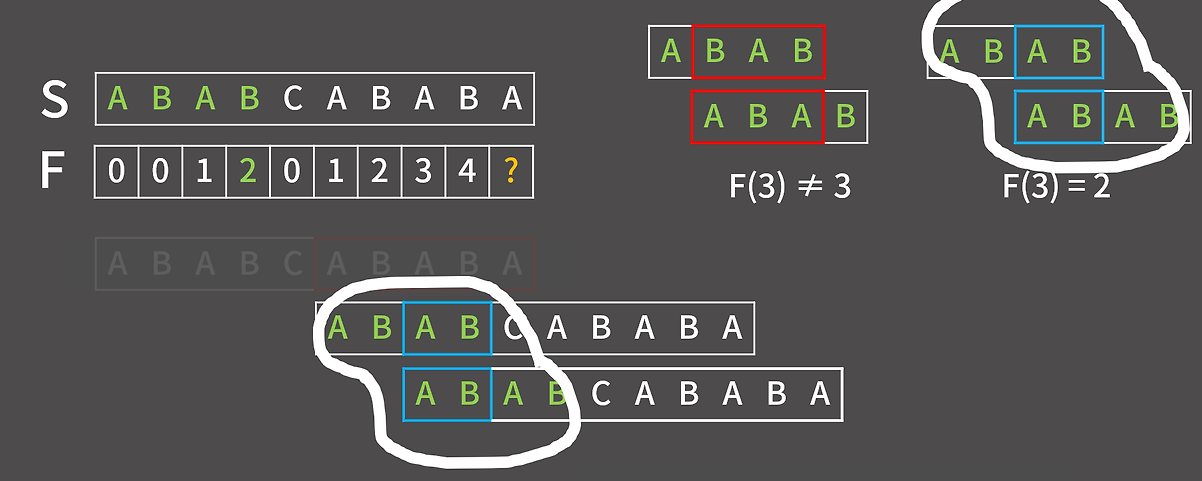
위 그림을 보면 F(6) = 2인데 전에 F(5)=1인 성질을 이용하여 구할 수 있다. F(5)가 1이므로 F(6)의 경우 접미사의 추가된 문자와 접두사를 F(5)에서 한 칸 뒤로 민 문자의 값과 동일한지만 비교하면 된다. 따라서 접미사의 추가된 문자와 현재 접두사의 다음 칸 문자가 동일하다면 F(N) = F(N-1)+1로 설정이 가능하다.

그런데 F(6)은 3이나 4처럼 크기를 늘려 비교할 필요는 없을까? 정답은 없다. 이는 귀류법으로 정리하여 설명할 수 있는데 만약 F(6)이 3이상일 경우 F(5)의 다음 F(6)에서 끝자리가 같을 때 F(6) = F(5)+1이므로 F(5)가 2 이상이여야 해서 모순이 발생함

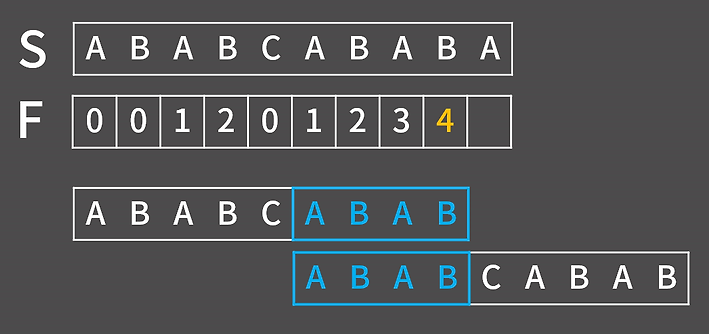
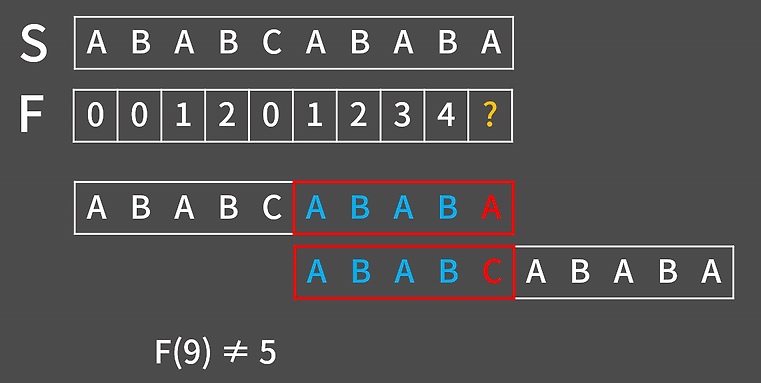
따라서 위와 같이 실패 함수를 채워가면 이러한 형태가 나오는데 위에서 설명한 방법과 다르게 F(9)의 경우 접미사 ABABA와 접두사 ABABC로 A와 C가 다른 상태여서 F(9)!=F(8)+1인 상태이다. 이럴 경우에 F(9)를 한 칸씩 밀면서 구하는 게 아닌 영리하게 구할 방법이 존재한다.

우선 F(8)의 경우 4개가 일치했던 사실은 이해가 됐을 것이다. 지금 마지막에 추가된 접미사와 접두사가 다른 상태이므로 F(9)를 구하기 위해선 접두사와 접미사의 위치를 조절해야 한다.

이 그림을 보면 어느 정도 감이 올 수 있는데 바로 인덱스의 위치를 이전 실패 함수의 위치로 변환하는 것이다.

• F(8) = 4 → 다시 F(4)로 점프
• F(4) = 2 → 접두사/접미사 "AB"가 다시 일치함을 확인
• 마지막 문자가 같으면 → F(9) = 2 + 1 = 3
• 마지막 문자가 다르면 F(4) = 2 → 다시 F(2)로 점프 ...
  결과적으로 F(9) = 3이 되는 것을 알 수 있다.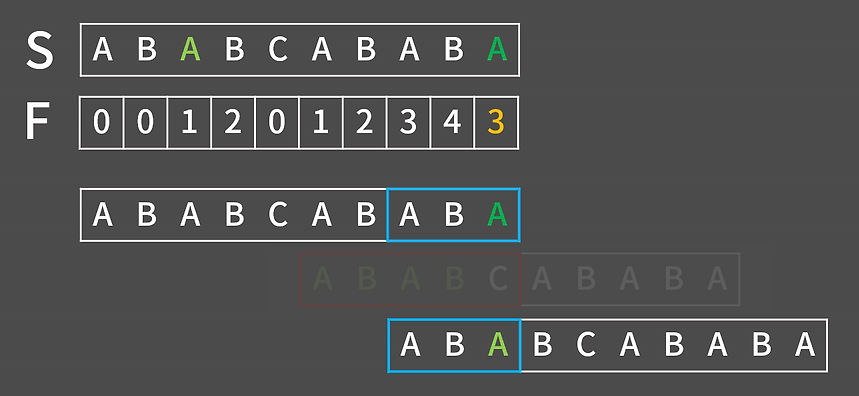

  

알고리즘

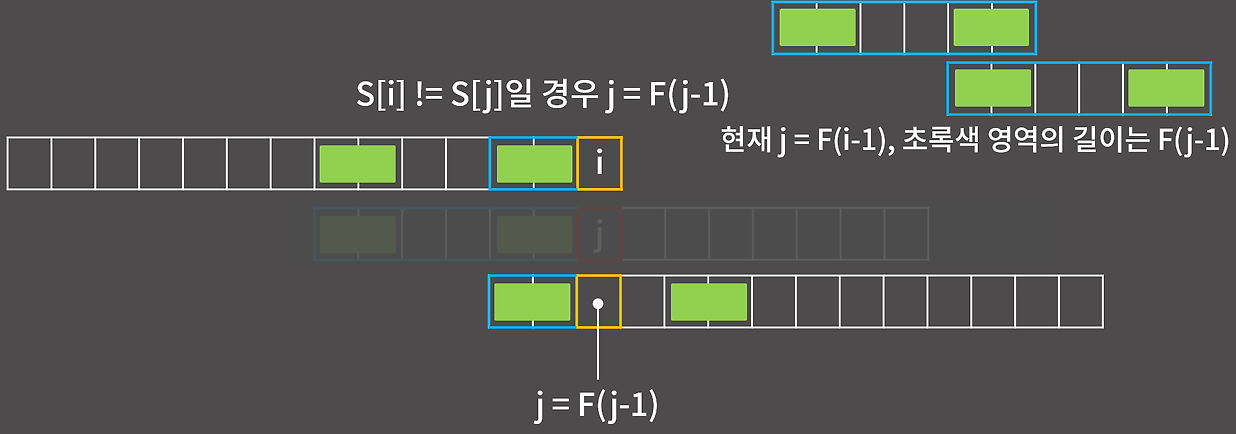
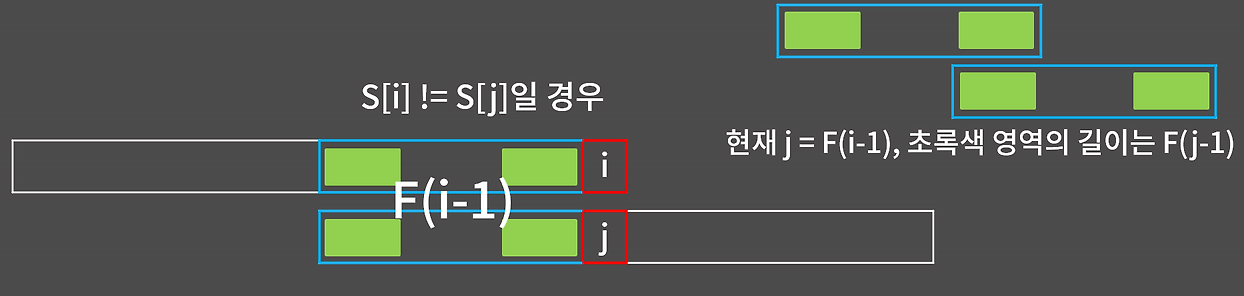
위와 같이 i,j라는 인덱스를 배치하여 같을 경우와 다를 경우를 생각하여 동작을 구현하면 다음과 같은 코드가 작성된다.

• 일치하는 경우: s[i] == s[j] → f[i] = ++j
• 불일치하는 경우: j > 0일 때 → j = f[j-1]로 점프해서 다시 비교

코드

vector<int> failure(string& s){
	vector<int> f(s.size());
    int j = 0;
    for(int i=1; i<s.size(); i++)
    {
    	while(j>0 && s[i] != s[j]) j = f[j-1];
        if(s[i] == s[j]) f[i] = ++j;
	}
    return f;
}

마무리

코드는 굉장히 간결하지만 이 작동 원리를 이해하기는 많이 어려웠다. 단순히 외우기보다는 원리를 그림으로 반복 학습하고 다양한 예제에 직접 적용해 보며 익혀가는 것이 핵심일 듯하다.

Reference
[실전 알고리즘] 0x1E강 KMP - BaaaaaaaarkingDog