다익스트라란?
1950년대에 에츠허르 다익스트라(Dijkstra)가 고안한 알고리즘으로 하나의 시작점에서 다른 모든 정점까지의 최단 경로를 구할 수 있는 방법이다.
Unity에서 AI가 플레이어를 쫓아올 때 장애물을 피하도록 설계하는 A* 알고리즘은 이 다익스트라 알고리즘을 기반으로 한 변형 알고리즘이다.
특히 다익스트라는 경로 탐색에도 매우 효과적인 알고리즘으로 널리 사용된다.
본론으로 돌아와 다익스트라 알고리즘을 구현하기 전에 알고리즘부터 설명하면 다음과 같다.
- 인접 리스트(vector)와 최단 거리 배열(d[])을 선언한다.
- 우선순위 큐(priority queue)에 시작 정점과 해당 코스트(거리)를 삽입한다.
- 큐가 빌 때까지 반복문을 실행한다.
3-1. 큐에 최상단(최소 코스트) 원소를 꺼내어 cur 변수에 추가하고 큐에서 삭제한다.
3-2. 만약 cur.cost가 현재 테이블에 저장된 d[cur 정점] 값과 다르면 이미 더 짧은 경로가 있다는 의미이므로 무시한다.(3-1로 다시 진행)
3-3. 현재 정점의 모든 인접 정점을 확인하여, d[cur] + 인접 cost < d[인접 정점] 조건을 만족하면 d배열을 갱신하고 큐에 {d[cur] + 인접 cost, 인접 정점}을 추가한다.
내용이 복잡하긴 하지만 핵심은 우선순위 큐를 통해 항상 최단 경로가 확정된 정점부터 처리한다는 점이다.
다만 주의할 점은 중복된 정점이 큐에 여러 번 들어갈 수 있기 때문에 3-2 조건을 반드시 넣어야 한다.
또한 3-3에서는 인접 cost만 넣는 게 아닌 현재까지의 최단 비용도 같이 넣어야 한다.
이제 동작 방식을 확인해 보자
1. 시작 정점 추가
우선순위 큐에 시작 정점을 삽입한다.
2. 인접 정점 추가
현재 정점의 모든 인접 정점을 탐색하여 거리를 계산해 큐에 추가한다.
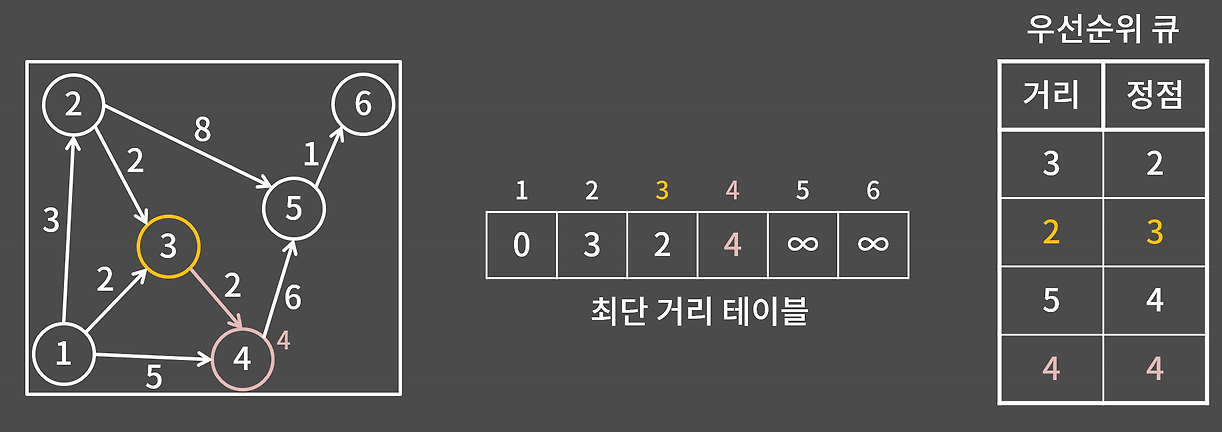
3. 최단 거리 선택
큐에서 가장 거리가 짧은 정점을 꺼내 인접 정점을 통해 더 짧은 경로가 있는지 확인한다.
4. 중복 정점 처리
같은 정점이 여러 번 큐에 들어가는 경우가 있다. 하지만 이미 더 짧은 경로로 처리된 경우 3-2 조건에 의해 무시된다.
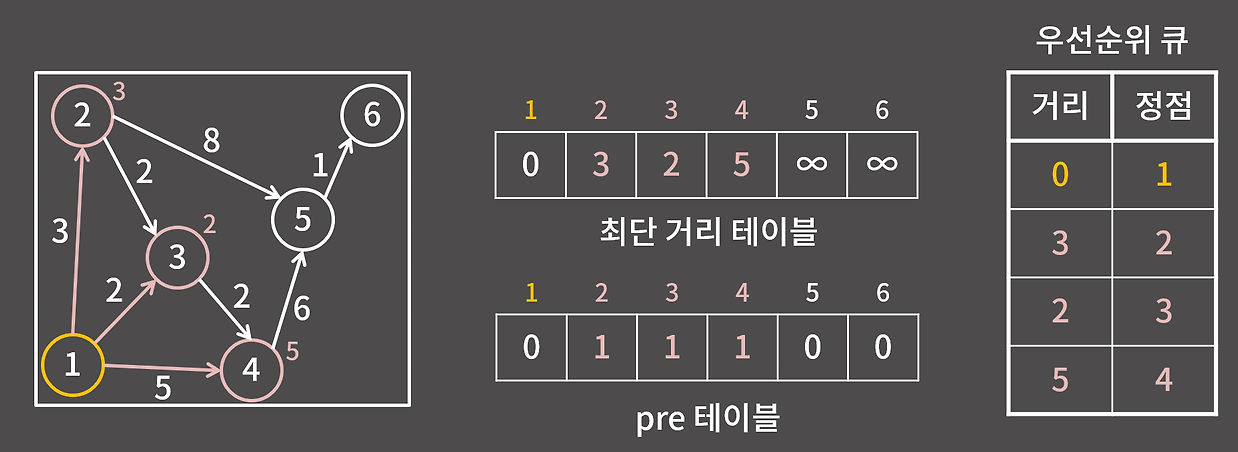
5. 완성된 최단 거리 테이블
모든 정점에 대해 최단 거리가 계산되면 다음과 같은 거리 테이블이 완성된다.
시간 복잡도
이렇게 우선순위 큐를 이용하여 다익스트라 알고리즘의 원리와 과정을 알아보았다.
시간복잡도의 경우 간선 1개당 1개의 원소가 추가되므로 O(ElgE)가 시간 복잡도이다.
경로 복원
다익스트라 알고리즘의 경우 시작 정점으로부터 모든 정점의 최단 거리를 구하는 알고리즘이다.
해당 알고리즘에서 시작 정점과 도착 정점이 주어질 때 경로를 구하는 방법이 존재한다.
이전 플로이드 알고리즘에서도 경로를 복원하기 위해 경로 테이블을 설정했던 것처럼 동일하게 경로 복원 테이블을 설정하여 값을 참조해 경로를 받아오는 것이다.
다익스트라의 경로 복원도 굉장히 간단하다. 알고리즘 자체는 다음과 같다.
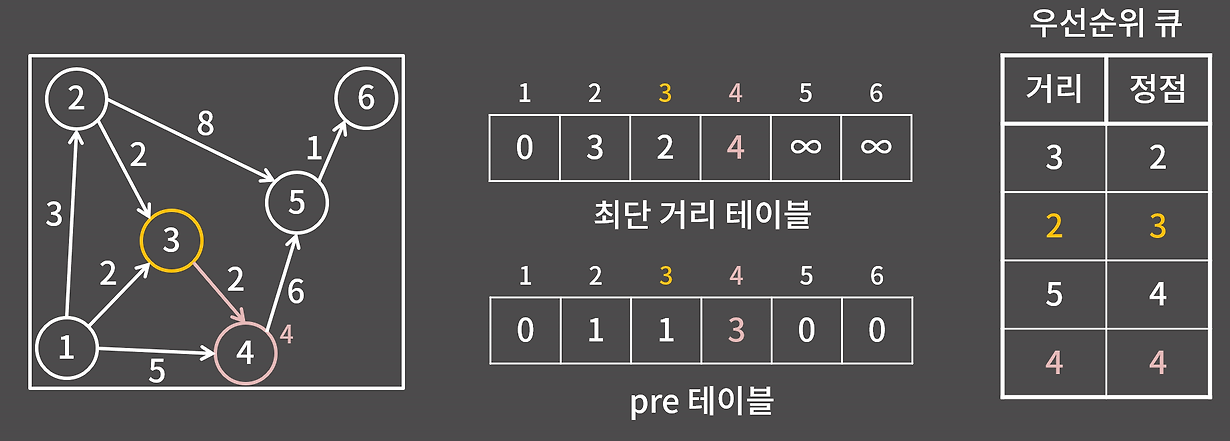
- 최단 거리 테이블을 갱신할 때마다 해당 정점으로 오기 직전 정점을 path[] 배열에 저장한다.
- 도착 정점에서 path[] 배열을 따라 시작 정점까지 경로를 추적한다.
이렇게 경로 복원 테이블의 경우 최단 거리 테이블이 갱신될 때마다 현재의 정점을 지정해 주면 쉽게 시작과 도착 지점의 경로를 알 수 있다.
위 그림과 최단 거리 테이블이 갱신됨에 따라 테이블을 같이 갱신해 주면 된다.
코드
#include <bits/stdc++.h>
using namespace std;
#define X first
#define Y second
#define pa pair<int,int>
priority_queue<pa, vector<pa>, greater<pa>> pq; // cost, vertex
vector<pa> adj[10002];
int d[10002];
int path[10002];
int v, e, st, en, inf=0x3fffffff;
void dijkstra()
{
while(!pq.empty())
{
auto cur = pq.top(); pq.pop();
if(cur.X != d[cur.Y]) continue;
for(auto c : adj[cur.Y])
{
if(d[cur.Y] + c.X < d[c.Y])
{
pq.push({d[cur.Y]+ c.X, c.Y});
d[c.Y] = d[cur.Y] + c.X;
path[c.Y] = cur.Y;
}
}
}
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cin >> v >> e;
fill(d, d+v+1, inf);
for(int i=0;i<e; i++)
{
int a, b, c;
cin >> a >> b >> c;
adj[a].push_back({c,b});
}
cin >> st >> en;
d[st] = 0;
pq.push({0,st});
dijkstra();
for(int i=1; i<=v; i++)
cout << d[i] << ' ';
cout << '\n';
int x = en;
vector<int> vec(1,x);
while(x != st)
{
x = path[x];
vec.push_back(x);
}
reverse(vec.begin(), vec.end());
for(auto c : vec)
cout << c << ' ';
return 0;
}
// Input
6 8
1 2 3
1 3 2
1 4 5
2 3 2
2 5 8
3 4 2
4 5 6
5 6 1
1 6
// Output
0 3 2 4 10 11
1 3 4 5 6 마무리
다익스트라 알고리즘은 전공 수업에서 자주 등장하지만 실제로 구현해 보면 생각보다 까다롭다.
특히, 우선순위 큐와 중복 조건을 처리하지 않으면 시간 초과가 발생할 수 있어 구현 세부 사항이 매우 중요하다.
이번에 직접 구현하면서 구조를 더 깊이 이해할 수 있었고 A* 알고리즘처럼 더욱 복잡했던 알고리즘도 어느 정도 흐름이 이해됐다.
앞으로도 다양한 알고리즘을 구현해 보며 실력을 키워나가야겠다고 느꼈다.
Reference
[실전 알고리즘] 0x1D강 다익스트라 알고리즘 - BaaaaaaaarkingDog