그래프

PKH·2025년 4월 27일

알고리즘

그래프란?

그래프란 정점(Vertex/Node)와 간선(Edge)으로 이루어진 자료구조이다.
그래프는 종류가 많고 개념도 다양하므로 하나씩 짚어 가보려 한다.

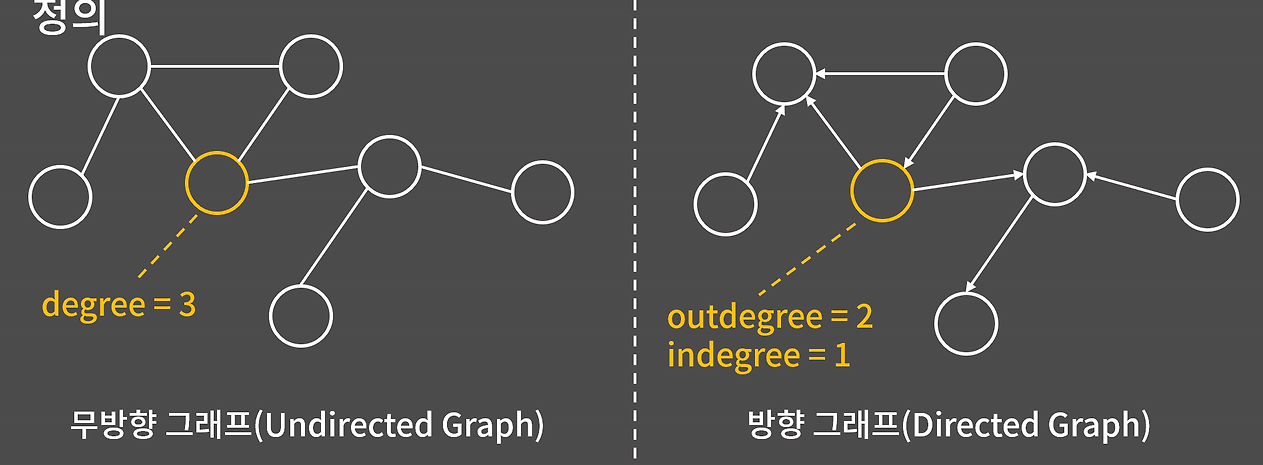
차수(Degree)

차수란 각 정점에 대해 간선으로 연결된 이웃 정점의 수를 의미한다.

무방향 그래프에서는 단순히 해당 노드에 연결된 간선의 수를 세면 된다.
방향 그래프에서는 정점으로 들어오는 간선의 수(In-degree)와 정점에서 나가는 간선의 수(Out-degree)를 구분한다.

그래프의 종류

그래프는 먼저 방향성 유무에 따라 구분할 수 있고 그 외에도 다양한 특성에 따라 여러 종류가 존재한다.

무방향 그래프(Undirected Graph) : 간선에 방향성이 없는 그래프

방향 그래프(Directed Graph) : 간선에 방향성이 존재하는 그래프

순환 그래프(Cyclic Graph) : 임의의 정점에서 출발해 다시 자기 자신으로 돌아올 수 있는 그래프

비순환 그래프(Acyclic Graph) : 순환 구조가 없는 그래프

완전 그래프(Complete Graph) : 모든 정점이 서로 연결된 그래프

연결 그래프(Connected Graph) : 임의의 두 정점 사이에 항상 경로가 존재하는 그래프
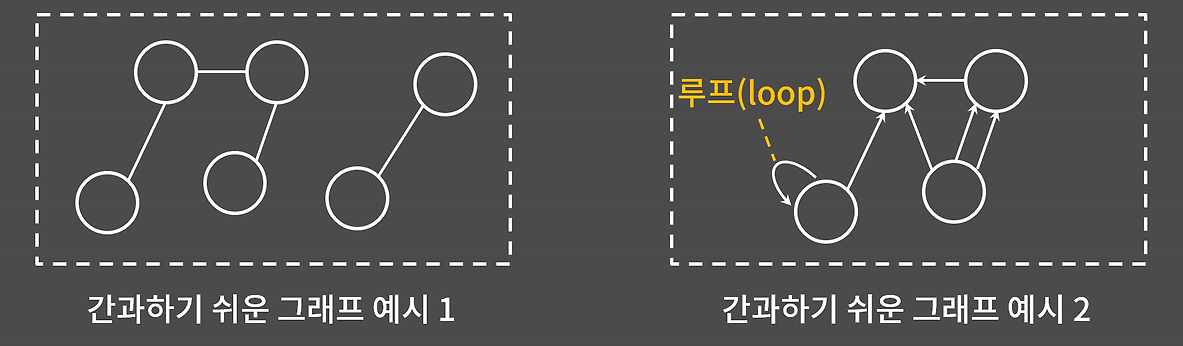
참고로 노드 사이에 연결이 끊어진 구간이 있거나 자기 자신을 향하는 간선이 있어도 그래프는 여전히 유효하다.

그래프의 표현법

그래프 개념을 이해하는 것도 중요하지만 이를 어떻게 코드로 구현할지를 아는 것도 매우 중요하다.
그래프를 표현하는 대표적인 방법은 다음 두 가지다.

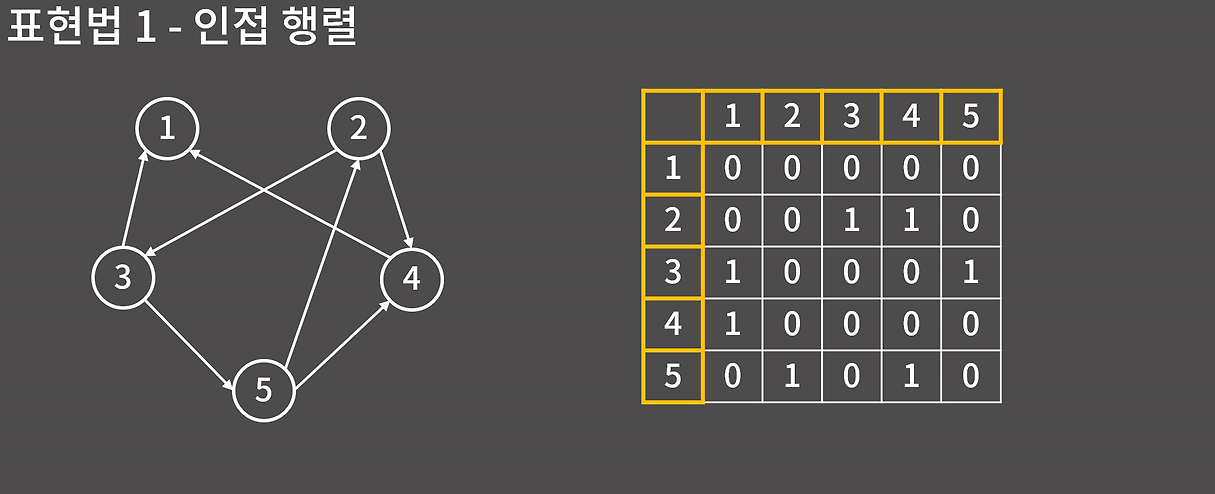
인접 행렬

인접 행렬은 각 노드에 대하여 2차원 배열 형태를 만들고 인접한 부분을 1로 변경하여 노드가 연결된 상태를 표현하는 방법이다.
만약 그래프가 방향 그래프라고 하면 양쪽 다 1로 만드는 형태가 아닌 한쪽만 1로 설정하면 된다.

코드

// 방향 그래프일 경우, 무방향이면 u와 v를 바꾼 배열도 1로 갱신
int adj_matrix[10][10];
int v, c;
cin >> v >> c;
for(int i=0; i<e; i++){
	int u, v;
    cin >> u >> v;
    adj_matrix[u][v];
}

인접 리스트

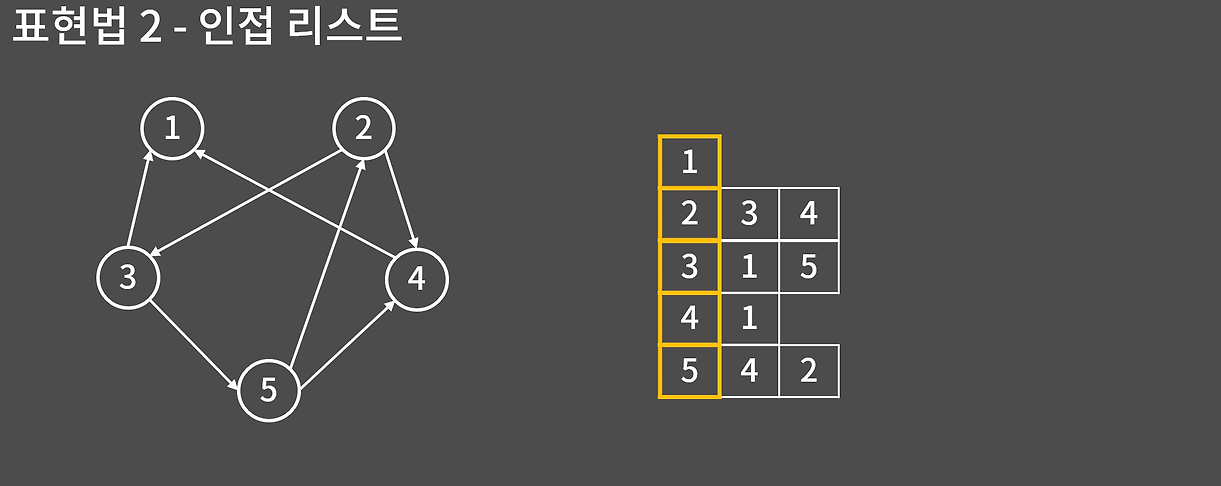
인접 리스트는 각 노드를 리스트 형태로 표현하고 해당 노드와 연결된 노드들을 저장하는 방식이다.
인접 리스트 같은 경우 인접 행렬과 비교하면 정점의 개수 2차원 배열로 갖는 O(V^2)가 아닌 각 정점에 대해 간선의 정보만큼 추가하는O(V*E) 공간을 가진다.

코드

// 방향 그래프일 경우, 무방향이면 u와 v를 바꾼 값도 벡터에 추가
vector<int> adj[10];
int v, e;
cin >> v >> e;
for(int i=0; i<e; i++){
	int u,v;
    cin >> u >> v;
    adj[u].push_back(v);
}

그래프 탐색

그래프에서 탐색은 크게 bfs와 dfs 2가지 방식을 사용한다.
bfs에서 4방향을 탐지했던 것과 다르게 queue에 시작할 노드를 추가하고 거기서부터 연결된 정점들을 탐지하면 된다.
dfs는 queue를 stack으로만 바꾸면 되지만 재귀를 써서 표현하는 경우가 더 쉽고 일반적으로 알고 있다. 다만 재귀는 매번 함수를 불러오며 스택 메모리를 생성하여 스택 메모리 초과를 유발할 경우도 많기 때문에 stack을 이용하여 구현하는 방법도 꼭 알아둬야 한다.

BFS

vector<int> adj;
bool vis[10];

void bfs(int st){
	queue<int> q;
    q.push(st);
    vis[st] = true;
    while(!q.empty()){
    	int v = q.front(); q.pop();
        for(auto av : adj[v]){
        	if(vis[av]) continue;
            q.push(av);
            vis[av] = true;
        }
    }
}

DFS

// 재귀를 안써는 경우
vector<int> adj;
bool vis[10];

void DFS(int st){
	stack<int> s;
    s.push(st);
    while(!s.empty()){
    	int v = s.top(); s.pop();
        if(vis[v]) continue;
        vis[v] = true;
        for(auto cv : adj[v])
        {
        	if(vis[cv]) continue;
            s.push(cv);
        }
    }
}

// 재귀
vector<int> adj;
bool vis[10];

void DFS(int st)
{
	if(vis[st]) return;
    vis[st] = true;
    for(auto cv : adj[st])
    {	
    	if(vis[cv]) continue;
        DFS(cv);
	}
}