트리란?
트리는 방향과 사이클이 없는 연결 그래프를 의미한다. 이 말이 직관적으로 와닿지 않을 수 있지만 일반적으로 우리가 떠올리는 트리 구조를 생각하면 이해하기 쉽다.
트리는 하나의 루트를 기준으로 부모-자식 관계가 형성되며 자식 노드끼리는 직접 연결되어 있지 않다. 이로 인해 사이클이 존재하지 않으며 트리 내의 어느 노드에서 다른 노드로 가는 경로가 항상 유일하게 존재한다.
다음은 트리의 특징이다.
- 방향과 사이클이 없는 연결 그래프이다.
- 임의의 간선을 제거하면 연결 그래프가 아니게 된다.
- 임의의 두 점을 연결하는 경로가 유일한 그래프
- V개 정점이면 간선은 V-1개
- 임의의 간선을 추가하면 반드시 사이클이 생김
아래는 동일한 트리 구조에서 서로 다른 정점을 루트로 삼아 표현한 예시이다.
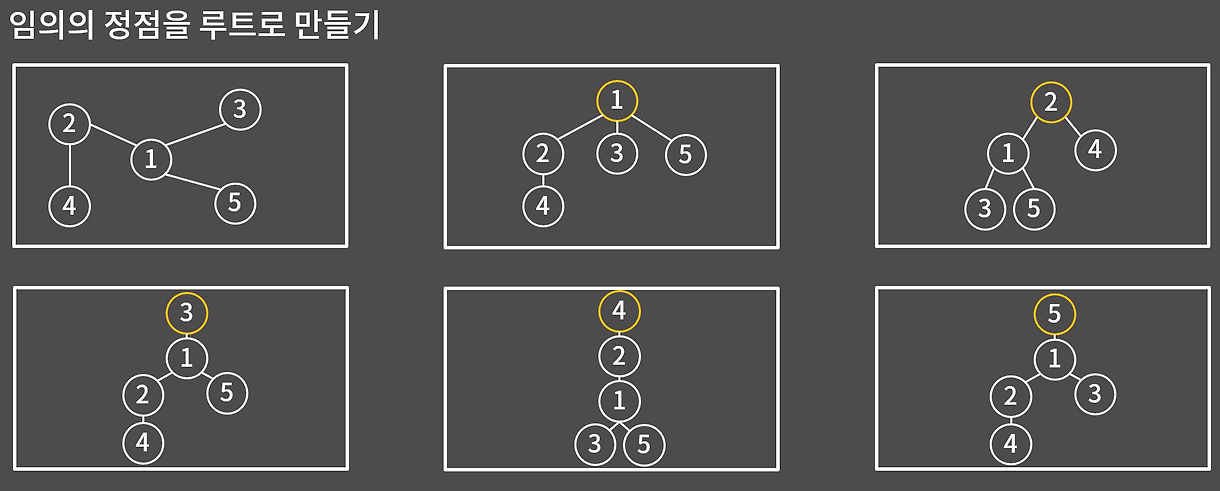
그림처럼 루트만 다를 뿐 모두 동일한 트리이며 어떤 정점을 루트로 삼아도 트리의 성립에는 문제가 없다.
순회
트리의 핵심은 순회이다. 트리 순회 방식은 크게 4가지로 나뉜다.
-레벨 순회 (Level-order)
-전위 순회 (Preorder)
-중위 순회 (Inorder
-후위 순회 (Postorder)
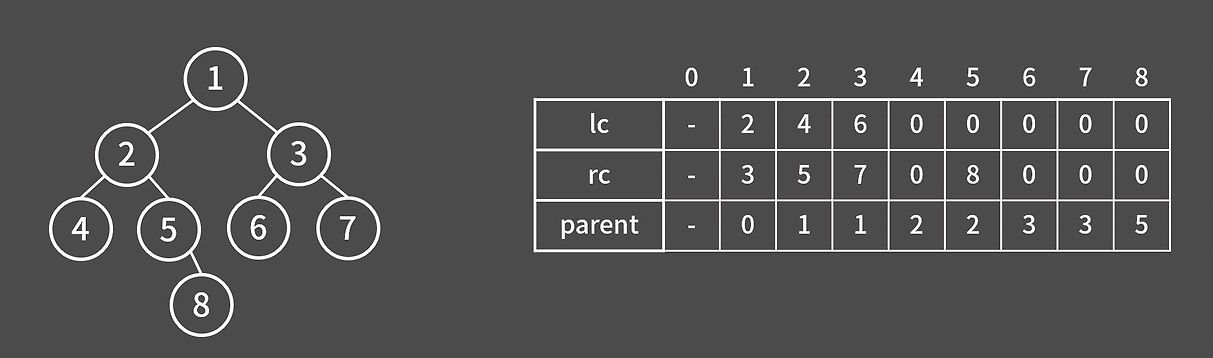
아래의 트리를 기준으로 각 순회 방법을 설명한다.
- 순회 예시 트리
그림처럼 자식과 부모는 주어진 상태로 코드를 작성
레벨 순회(Level-order Traversal)
루트부터 시작해 위에서 아래로 그리고 왼쪽에서 오른쪽으로 순회하는 방식이다. BFS 방식과 유사하며 Queue를 사용한다.
- BFS를 위해 Queue를 선언하고 루트를 집어넣는다.
- 큐에서 노드를 꺼내 출력
- 해당 노드의 왼쪽 자식, 오른쪽 자식을 Queue에 삽입
- Queue가 빌 때까지 위 작업을 반복
#include <bits/stdc++.h>
using namespace std;
int l[10] = {0,2,4,6,};
int r[10] = {0,3,5,7,0,8,};
int p[10] = {0,0,1,1,2,2,3,3,5,};
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
queue<int> q;
q.push(1);
while(!q.empty())
{
int cur = q.front(); q.pop();
cout << cur << ' ';
if(l[cur]) q.push(l[cur]);
if(r[cur]) q.push(r[cur]);
}
return 0;
}
// Output
// 1 2 3 4 5 6 7 8 전위 순회(Preorder Traversal)
전위 순회는 말 그대로 가장 앞에서부터 순회를 진행한다고 생각하면 된다.
즉 지금 가장 앞에라는 말은 지금 방문한 노드를 의미하는 것과 동일하여 DFS 방식과 동일하다.
- 현재 방문한 노드를 출력한다.
- 왼쪽 서브 트리를 방문한다.
- 오른쪽 서브 트리를 방문한다.
// stack 방식
#include <bits/stdc++.h>
using namespace std;
int l[10] = {0,2,4,6,};
int r[10] = {0,3,5,7,0,8,};
int p[10] = {0,0,1,1,2,2,3,3,5,};
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
stack<int> s;
s.push(1);
while(!s.empty())
{
int cur = s.top(); s.pop();
cout << cur << ' ';
if(r[cur]) s.push(r[cur]);
if(l[cur]) s.push(l[cur]);
}
return 0;
}
// Output
// 1 2 4 5 8 3 6 7 // 재귀 방식
#include <bits/stdc++.h>
using namespace std;
int l[10] = {0,2,4,6,};
int r[10] = {0,3,5,7,0,8,};
int p[10] = {0,0,1,1,2,2,3,3,5,};
void Preorder(int st)
{
cout << st << ' ';
if(l[st]) Preorder(l[st]);
if(r[st]) Preorder(r[st]);
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
Preorder(1);
return 0;
}
// Output
// 1 2 4 5 8 3 6 7 중위 순회(Inorder Traversal)
중위 순회 방식은 전위랑 다르게 왼쪽 서브 트리-현재 노드-오른쪽 서브 트리 순으로 가장 맨 왼쪽부터 방문한다고 생각하면 된다.
즉 전위 순회 방식에서 현재 노드 출력과 왼쪽 서브 트리의 방문 순서만 바꾸면 된다.
- 왼쪽 서브 트리 방문
- 현재 노드 출력
- 오른쪽 서브 트리 방문
#include <bits/stdc++.h>
using namespace std;
int l[10] = {0,2,4,6,};
int r[10] = {0,3,5,7,0,8,};
int p[10] = {0,0,1,1,2,2,3,3,5,};
void Inorder(int st)
{
if(l[st]) Inorder(l[st]);
cout << st << ' ';
if(r[st]) Inorder(r[st]);
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
Inorder(1);
return 0;
}
// Output
// 4 2 5 8 1 6 3 7 후위 순회(Postorder Traversal)
후위 순회는 전위와 중위의 동작 순서를 확인해 보면 후위는 어느 정도 감이 올 수 있다.
바로 현재 정점을 가장 마지막에 방문하는 것이 후위 순회이다.
- 왼쪽 서브 트리 방문
- 오른쪽 서브 트리 방문
- 현재 노드 출력
#include <bits/stdc++.h>
using namespace std;
int l[10] = {0,2,4,6,};
int r[10] = {0,3,5,7,0,8,};
int p[10] = {0,0,1,1,2,2,3,3,5,};
void Postorder(int st)
{
if(l[st]) Postorder(l[st]);
if(r[st]) Postorder(r[st]);
cout << st << ' ';
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
Postorder(1);
return 0;
}
// Output
4 8 5 2 6 7 3 1마무리
이번에 트리에 대해 공부하면서 기존에 알고 있던 내용을 다시 정리하는 좋은 기회가 되었다. 특히 트리 순회의 다양한 방식과 구현을 코드로 직접 확인해 보니 이해가 훨씬 더 잘 되었다.
아직 트리 관련 문제를 많이 풀어보진 못했지만 앞으로 다양한 문제를 접하면서 트리에 대한 응용력과 깊이를 더욱 키워나갈 예정이다.
Reference
[실전 알고리즘] 0x19강 트리 - BaaaaaaaarkingDog