소수

사실 수학 파트는 알고리즘으로 분류하기 조금 고민됐으나 가장 기본적이고 중요한 내용들을 정리하므로 이 또한 알고리즘 파트에 넣었다.

소수란?

소수는 1과 자기 자신 이외의 나누어떨어지는 수가 없는 수를 얘기한다. 대표적으로 2,3,5,7... 이렇게 쭉 이어지는데 컴퓨터는 소수인지 어떻게 판별할까?
가장 기초적인 방법으로는 n이 소수인지 판별하기 위해 2부터 n-1까지 n을 나눠보고 나누어지는지를 파악하여 소수를 판별한다.

bool isprime(int n)
{
	if(n==1) return 0;
    for(int i=2; i<n; i++)
    	if(n%i == 0) return 0;
    return 1;    
}

이 방법은 1을 제외한 n-2번의 나눗셈 연산을 수행하므로, 시간 복잡도는 O(n)이다. 하지만 이보다 더 효율적인 방법이 존재한다. 이를 설명하기 전에 소수와 합성수를 간단히 정리하자.

• 소수 : 1과 자기 자신 외에 나누어떨어지는 수가 없는 수
• 합성수 : 1과 자기 자신 외에 다른 약수를 가지는 수

합성수의 특징을 이용하면 소수를 더 빠르게 판별할 수 있다. 합성수의 가장 작은 약수는 항상 $\sqrt{n}$ 이하이다.

합성수에서 n에서 1을 제외한 가장 작은 약수는 $\sqrt{n}$이하이다.

증명

1. n에서 1을 제외한 가장 작은 약수를 x라고 가정
2. n/x도 n의 약수가 된다. (약수의 대칭성: x가 n의 약수이면, n/x도 n의 약수)
3. n/x >= x이고 이를 전개하면 n > x^2 따라서 x <= $\sqrt{n}$ 이라는 결론 도출

이 성질을 이용하면 소수를 O(n) 대신 O($\sqrt{n}$)의 시간 복잡도로 판별할 수 있다.

bool isprime(int n)
{
	if(n==1) return 0;
    for(int i=2; i*i<=n; i++){
    	if(n%i==0) return 0;
    }
    return 1;
}

해당 함수에 대한 설명을 조금 더 하자면 다음과 같이 정리할 수 있다.

• 먼저 컴퓨터의 실수 계산은 정확하지 않기 때문에 sqrt함수를 쓰지 않고 제곱하여 for문을 작성했다.
• 범위가 $\sqrt{n}$(i*i<=n)인 이유는 $\sqrt{n}$보다 큰 약수만으로는 n을 구성할 수 없으며, $\sqrt{n}$ 이하의 수로 나누어떨어지지 않는다면 소수임이 보장되기 때문이다.

에라토스테네스의 체

에에라토스테네스의 체는 소수를 빠르게 구하는 대표적인 방법 중 하나다. 원리는 간단하다. 소수인지 여부를 판단한 후 해당 수의 배수를 모두 제거하는 방식이다.

1은 소수가 아니므로 처음부터 제외한다.

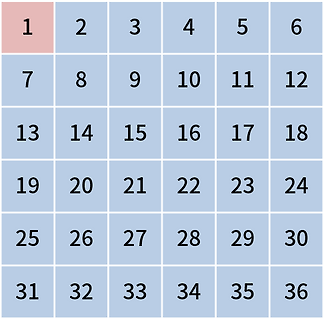
2는 소수이므로 남겨두고, 2의 배수를 모두 제거한다.

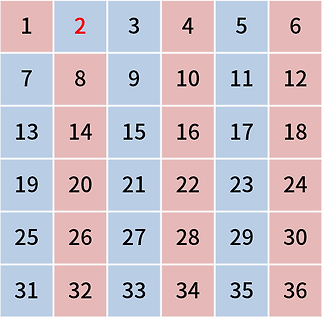
3도 마찬가지로 소수이므로 남겨두고, 3의 배수를 제거한다. 이미 소수가 아닌 것으로 판정된 수는 건너뛴다.
이 과정을 반복하면 n 이하의 모든 소수를 구할 수 있다.

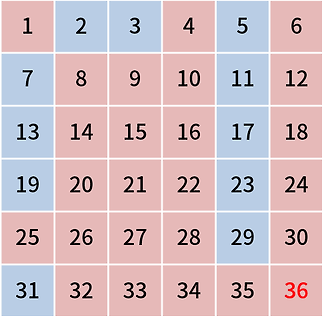
에라토스테네스의 체를 코드로 작성하면 다음과 같이 작성할 수 있다.

vector<int> isprime(int n)
{
	vector<int> primes;
    vector<bool> states(n+1, true); // 0~n까지 크기를 설정하고 초기값을 true로 설정
    states[1] = false;
    for(int i=2; i<=n; i++){
    	if(!states[i]) continue; // 이미 소수가 아니라면 다음 수로 넘어감
        for(int j=i*2; j<=n; j+=i) // i의 배수를 모두 소수가 아닌 수로 설정 
        	states[i*j] = false;
    }
    for(int i=2;i<=n;i++)
    	if(states[i]) primes.push_back(i);
    return primes;
}

에라토스테네스의 체를 구현했으나 5의 경우를 보면 10과 15는 이미 false가 돼 있는 상태에서 중복 계산을 진행하므로 효율적이지 않다. 따라서 이 코드 또한 더 개선하여 시간복잡도를 줄일 수 있다. 위에서 다루었던 합성수를 이용한 $\sqrt{n}$방법을 적용하는 것이다.

vector<int> isprime(int n)
{
	vector<int> primes;
    vector<bool> states(n+1,true);
    
    states[1] = 0
    for(int i=2; i*i<=n; i++)
    {
    	if(!states[i]) continue;
        for(int j=i*i; j<=n; j+=i)
        	states[i] = false;    
    }
    for(int i=2; i<=n;i++)
    	if(states[i]) primes.push_back(i);
    return primes;
}

소인수분해

소수하면 같이 빠지지 않는 소인수 분해가 존재한다. 소인수분해는 소수의 곱으로 나타내는 것을 의미한다.
위에서 공부했던 내용을 기반으로 1100이라는 수를 소인수분해하는 코드를 작성해 보려고 한다.
먼저 1100 = 2*2*5*5*11이다. 이 1100을 소인수 분해하는 과정을 잘 생각해 보면 이런 단계로 나누어 질 것이다.

1. 2 * 550
2. 2 * 2 * 275
3. 2 * 2 * 5 * 55
4. 2 * 2 * 5 * 5 * 11

위 과정을 보면 계속해서 소수의 크기를 늘려가며 나눈 것을 알 수 있다. 이를 바탕으로 소인수 분해 코드를 작성하면 다음과 같다.

vector<int> factorization(int n)
{
	vector<int> vec;
    
    for(int i=2; i*i<=n; i++)
    {
    	while(n%i !=0)
        {
        	vec.push_back(i);
            n /= i;
        }
    }
    
    if(n!=1) vec.push_back(i);
    
    return vec;
}

마무리

해당 파트는 실질적인 알고리즘보단 수학적인 개념을 이용하여 문제를 해결하는 알고리즘을 공부했다. 이 소수 파트는 그렇게 정리를 하였는데 앞으로도 수학적 개념을 이용하여 문제를 해결하는 문제들이 나온다면 이런 식으로 정리를 해보려고 한다.

Reference
[실전 알고리즘] 0x12강 수학 - BaaaaaaaarkingDog