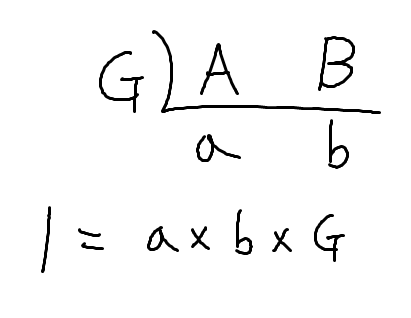약수

약수란?

약수는 어떤 수를 나누어떨어지게 하는 수를 의미한다. 예를 들자면 18의 경우 1,2,3,6,9,18이 약수가 된다.
이를 구하는 방법은 1부터 n까지 돌리는 방법이 있지만 지난번 소수를 공부할 때 합성수의 약수의 대칭성을 이용하여 1,2,3만 구하면 나머지 6,9,18은 18/(1,2,3)으로 구할 수 있다.
따라서 시간복잡도 또한 O($\sqrt{n}$)으로 설정이 가능하다.
해당 약수를 코드로 작성하면 다음과 같이 작성할 수 있다.

vector<int> divisor(int n){
	vector<int> vec;
    for(int i=1; i*i<=n; i++)
    {
		if(n%i==0) vec.push_back(i);
	}
    for(int i=(int)vec.size()-1; i>=0; i--) // (int)는 overflow방지
    {
    	if(vec[i]*vec[i] == n) continue; // 약수가 자기 자신을 쌍으로 이루는 경우
    	vec.push_back(n/vec[i]);
    }
    
    return vec;
}

GCD란?

GCD는 Greatest Common Divisor로 두 자연수의 공통된 약수 중 가장 큰 약수로
즉, 최대 공약수를 의미한다.

20과 12가 있다면
20의 약수 = 1,2,4,5,10,20
12의 약수 = 1,2,3,4,6,12
1,2,4의 공통된 약수중 최대인 4가 GCD(최대 공약수)가 된다.
이를 코드로 구현하기 전에 GCD는 아주 쉬운 공식이 있다 바로 A,B의 최대 공약수는
B와 A를 B로 나눈 나머지(= A%B)의 최대 공약수와 값이 동일하다는 것이다. 이 유명한 방법은 유클리드 호제법인데 증명은 다음과 같다.

GCD 증명

A와 B의 최대공약수를 x라고 지정하고 A>=B로 가정
A = ax
B = bx (a와 b는 x가 최대 공약수이므로 서로소임)
A = QB + R (Q : A를 B로 나눈 몫, R : A를 B로 나눈 나머지)
ax = Qbx + R
R = ax - Qbx = x(a-Qb)
즉 R과 B의 관계에서 a-Qb와 b가 서로소일 경우 x의 최대 공약수가 생김
이를 증명하기 위해 반대로 a-Qb와 b가 서로소가 아닐 경우에 생기는 모순을 증명
a-Qb와 b가 서로 최대공약수 m을 가진다고 가정
a-Qb = mk
b = mb1
a-Qmb1 = mk -> a = Qmb1 +mk = m(Qb1 + k)
여기서 a와 b는 서로소인데 현재 관계에 적용해 보면 다음과 같음
1) m != 1 일때, m이 1이상 수를 가지므로 a와 b의 공통된 약수 m이 생김 (a,b 서로소 모순)
2) m==1 일때, Qb1 + k와 b1이 서로소가 아니어야 함
a = Qb1 + k
b = b1
k가 위에서 mk = a -Qb였으나 m이 1이므로 k = a -Qb가 됨
a = Qb1 + k = Qb + a - Qb = a
즉 Qb1 + k와 b1은 각각 a와 b가 되며 이는 모순이 발생함(Qb1 + k , b1 서로소 모순(=a,b) a와b는 서로소라고 맨 위에서 정의한 것과 모순됨)
이로써 a-Qb와 b가 서로소가 아닐 경우엔 모순이 발생하므로 결국 a-Qb와 b는 서로소가 됨
따라서 B와 R의 최대공약수도 x이므로 유클리드 호제법 공식이 증명됨

증명이 생각보다 많이 길어졌지만 이로써 A와B의 최대공약수는 B와 A%B의 최대공약수와 동일함을 알 수 있다. 따라서 이는 20와 12을 GCD에 대입하면 GCD(20,12) = GCD(12,8) = GCD(8, 4) = GCD(4, 0)이므로 0과 최대 공약수를 구할 수 없으므로 마지막 나머지였던 4가 최대공약수가 된다.
이를 코드로 구현하면 간단하다

int GCD(int a, int b){
	if(b==0) return a;
    return GCD(b,a%b);
}

코드를 보면 알겠지만 만약 그러면 (12,20)으로 a<=b인 경우에는 알아서 자리가 바뀌며 (20,12)로 다시 설정되기 때문에 걱정할 필요가 없다.

LCM이란?

LCM은 Least Common Multiple로 두 수에서 서로 공통으로 존재하는 가장 작은 배수로 최소공배수를 의미한다.
LCM은 A와B의 최소 공배수는 A와 B를 곱한 수에서 최대 공약수를 나눈 것과 동일하다.
즉 LCM = A * B / GCD(A,B)이다. 이유는 A * B = GCD(A,B) * LCM(A,B)가 동일하기 때문이다.

증명
A와 B가 최대공약수 G를 가진다고 가정
A = Ga
B = Gb (a와 b는 서로소)
최소공배수 l이라고 가정
l = G * a *b
여기 까진 아마 최소 공배수공식을 생각하면 쉽게 구할 수 있을 것이다.

이제 이걸 식으로 정리하면 증명이 끝난다. 먼저 양변에 G를 곱한다
l * G = G * a * G * b = A * B
따라서 최소 공배수 l = A * B / G 라는 식이 나온다.
(즉, LCM(A,B) = A * B / GCD(A,B))

증명은 되게 간단했다. 이제 이를 코드로 작성하면 다음과 같다

int LCM(int a, int b){
	return A / GCD(A,B) * B; 
}

코드에서 중간에 GCD를 가운데로 옮긴 이유는 overflow를 방지하기 위해서이다
단순하게 a와 b가 서로 1억씩만 된다 하더라도 a * b값에서 overflow가 발생하므로 GCD를 먼저 나눈 것이다.

연립합동방정식

연립합동방정식은 방정식 중에서 복수의 방정식이 세트로 묶여 있는 것을 의미한다.
문제를 보면 더 쉽게 이해할 수 있다.

이러한 문제가 있다 만약 이 반 학생들의 수를 구하기 위해 우리가 코드로 작성하려고 한다.
아마 학생 수가 1일 때부터 30명 미만일 때까지 인원수를 늘리면서 다음 조건에 맞는 조건식을 설정하면 학생 수를 쉽게 구할 수 있을 것이다.

다음과 같이 작성할 수 있다.

int student(int n){
	for(int i=1; i<n; i++){
    	if(i%5==2 && i%6==3) return i;	
    }
    return -1;
}

그런데 이 코드에서 더 쉽고 빠르게 찾는 방법이 존재한다. 바로 나머지에 집중하는 것이다.
현재 1부터 30명 미만일 때까지 학생 수를 증가시키면서 찾는 방법이 아니라 6명씩 조를 형성했을 때 남은 학생 수가 3인 경우를 나열하고 그중에서 5명으로 나눴을 때 남은 학생 수가 2인 값을 찾으면 되는 것이다.

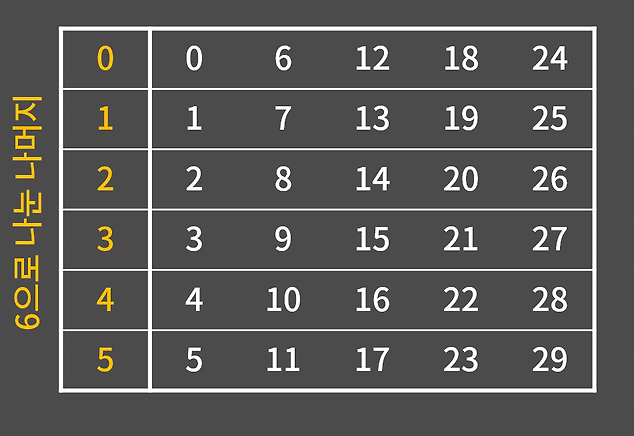
이를 코드로 작성하면 다음과 같다.

int student(int n){
	for(int i=3; i<n; i+=6){
		if(n%i==2) return i;
	}
    return -1;
}

마무리

수학적 증명을 오랜만에 딥하게하여 머리를 많이 쓴 것이 느껴진다. 아무래도 다른 사람들의 정보 없이는 쉽게 증명할 수 없었을 것이다. 또한 위 내용들은 코딩테스트에서 많이 나오는 유형은 아니지만 어찌 보면 기초로 여겨지는 만큼 중요한 개념이라 생각하여 까먹지 않도록 자주 복습을 해야겠다.

Reference
[실전 알고리즘] 0x12강 수학 - BaaaaaaaarkingDog