배달 (Dijkstra)

하루히즘·2021년 4월 28일

프로그래머스

목록 보기

2/17

설명

프로그래머스의 배달 문제다.

주어진 비방향 가중치 그래프에서 출발 노드로부터 일정 비용 이내로 도달할 수 있는 노드들의 갯수를 세는 것이 목적이다. 이전에 풀었던 그래프 문제들은 노드의 연결 정보만 주어졌기 때문에 하나의 사전 자료형을 이용하여 풀 수 있었지만 이번에는 가중치도 같이 주어지기 때문에 별도의 자료구조로 이를 유지해야 한다.
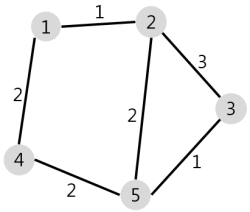예를 들어 위와 같은 그래프가 주어질 때 1번 노드에서 3의 비용으로 도달할 수 있는 노드는 1, 2, 4, 5가 될 것이다.

이는 결국 1번 노드부터 다른 노드까지의 최단거리를 구하는 것과 동일하다. 처음에는 DFS 탐색을 시도했지만 몇 개의 테스트 케이스가 계속 실패했기 때문에 조사해본 결과 다익스트라 알고리즘을 사용하여 풀어야 한다는 것을 알 수 있었다.

다익스트라는 아직 공부하지 않았기 때문에 이곳을 참조하여 풀 수 있었다.

풀이

DFS 탐색(실패)

처음으로 시도했던 DFS 탐색 방식이다. 1번 노드부터 일정 비용 이내로 도달할 수 있는 노드를 탐색한다는 것에서 착안하여 재귀 호출을 이용한 DFS 탐색으로 구현하였는데 아쉽게도 몇몇 테스트 케이스를 실패했다.

import collections


def solution(N, road, K):
    global costs, links, max_cost
    
    # 노드 i부터 노드 j까지 이동하는 비용을 저장하는 사전 자료형.
    # 키로 노드 i, 값으로 다른 노드까지 이동하는 비용의 리스트를 저장.
    # ex) costs[1][3]: 노드 1에서 노드 3까지 이동하는 비용.
    costs = {village: [10001]*(N+1) for village in range(1, N+1)}        
    # 노드 i에서 이동할 수 있는 이웃 노드들을 저장하는 사전 자료형.
    # 키로 노드 i, 값으로 이웃 노드를 담는 set을 저장.
    links = collections.defaultdict(set)
    # 한계 비용.
    max_cost = K
    
    # 주어진 그래프 정보를 읽어서 구축.
    for road_info in road:
        departure, destination, cost = road_info
        # 비방향이기 때문에 이웃 노드들을 양쪽 노드에 구축.
        links[departure].add(destination)
        links[destination].add(departure)
        # 마찬가지로 비용도 양쪽 노드에 구축.
        # 노드 간 비용은 여러번 주어질 수 있기 때문에 최소의 비용으로 설정.
        costs[departure][destination] = min(cost, costs[departure][destination])
        costs[destination][departure] = min(cost, costs[destination][departure])
    
    # 한계 비용을 넘지 않고 방문할 수 있는 노드들의 집합.
    availables = set()
    for neighbor in links[1]: # 1번 노드의 이웃 노드부터 탐색.
        # 각 이웃 노드마다 탐색한 결과를 방문할 수 있는 노드들의 집합에 합산.
        visited = set([1])
        find_available_villages(costs[1][neighbor], neighbor, visited)
        
        availables = availables.union(visited)
    
    # 방문할 수 있는 노드들의 갯수를 반환.
    return len(availables)


def find_available_villages(current_cost, current_village, visited_villages):
    # 현재 노드까지 도달한 비용이 한계 비용을 초과했거나 이미 방문한 노드일 경우 중단.
    if current_cost > max_cost or current_village in visited_villages:
        return
    
    # 방문한 노드 집합에 현재 노드를 추가.
    visited_villages.add(current_village)
    
    # 현재 노드의 이웃 노드에 다시 재귀 호출 탐색.
    for neighbor in links[current_village]:
        # 현재까지의 비용과 이웃 노드의 이동 비용의 합을 전달.
        find_available_villages(current_cost + costs[current_village][neighbor], neighbor, visited_villages)

프로그래머스는 따로 테스트 케이스를 보여주지 않기 때문에 무슨 반례가 있었는지는 영원히 알 수 없을 것이다.

Dijkstra 알고리즘

언급했듯이 이 풀이는 다른 블로그의 풀이를 그대로 작성한 것이다. 이해를 위해 한 줄씩 직접 작성하였고 위키피디아에 정의된 다익스트라 알고리즘과 비교하면서 학습하였다.

다익스트라 알고리즘은 다음과 같다.

모든 노드를 방문하지 않은 노드로 정의한다.
시작 노드에서 각 노드까지의 거리를 시작 노드(이 문제에서는 노드 1)는 최솟값으로, 나머지는 최댓값으로 저장한다.
초기 노드부터 시작하여 현재 노드의 이웃 노드를 다음과 같은 과정으로 탐색한다.
- 초기 노드에서 해당 이웃 노드까지의 거리를 tentative라 한다.
- 초기 노드에서 현재 노드까지의 거리와 현재 노드에서 이웃 노드까지의 거리의 합을 calculated라 한다.
- 즉 기존에 계산된 거리와 지금 상황에서 다시 계산한 거리를 비교하는 것이다.
- tentative가 calculated보다 크다면 해당 이웃 노드까지 이동할 수 있는 최단거리가 갱신되었다는 것이므로 초기 노드에서 해당 이웃 노드까지의 거리를 calculated로 갱신한다.
- 현재 노드를 방문한 노드에 추가한다.
- 이후 노드를 탐색하면서 방문한 노드거나 이웃 노드가 없다면 탐색을 종료한다.

이런 다익스트라 알고리즘을 위 문제에 어떻게 적용할 수 있을까? 이 문제에서는 배달 비용 제한이 주어진다. 즉 현재 노드가 방문했던 노드인 것 뿐 아니라 현재 노드까지 탐색 비용이 한계를 초과한다면 탐색을 종료하는 조건을 추가해주면 된다.

import collections


def solution(N, road, K):
    # 기준 노드부터 다른 노드까지 최종 비용을 저장하는 배열.
    # costs[i] = 1번 노드에서 i번 노드까지의 이동 비용.
    costs = [500001] * (N+1)
    costs[1] = 0
    
    # 현재 노드의 이웃 노드 목록을 저장하는 집합.
    # links[i] = i번 노드의 이웃 노드 집합.
    links = collections.defaultdict(set)
    
    # 한 노드에서 이웃 노드까지 이동하는 비용을 저장해 둔 배열.
    # fees[i][j] = i번 노드에서 j번 노드까지 이동하는 비용.
    fees = [[]]
    for _ in range(N):
        fees.append([10001] * (N+1))
    
    # 문제에서 주어진 그래프 정보를 파싱.
    for road_info in road:
        departure, destination, fee = road_info
        # 비방향이기 때문에 양쪽 노드 모두에 등록.
        links[departure].add(destination)
        links[destination].add(departure)
        
        # 노드 간 이동 거리는 복수가 주어질 수 있기 때문에 그중 최소값 사용.
        fees[departure][destination] = min(fee, fees[departure][destination])
        fees[destination][departure] = min(fee, fees[destination][departure])
    
    # 탐색을 위한 큐(데크) 구축.
    queue = collections.deque()
    queue.append(1)
    
    # 다익스트라 알고리즘 기반 탐색 진행.
    while queue:
        current_village = queue.popleft()
        # 현재 노드의 이웃 노드들에 대하여 탐색.
        for neighbor in links[current_village]:
            # 기존에 파악된 비용과 현재 노드에서 다시 계산된 비용 비교.
            cost = costs[current_village] + fees[current_village][neighbor]
            # 현재 노드에서 이웃 노드로 이동하는 비용: cost
            # 다른 노드에서 계산된 해당 노드로 이동하는 비용: costs[neighbor]
            # 다른 노드에서 이웃 노드로 이동하는게 더 적은 비용이라면 탐색하지 않음.
            # 또는 이동 비용이 문제에서 요구하는 한계를 초과하면 탐색하지 않음.
            if cost >= costs[neighbor] or cost > K:
                continue
            
            # 위의 조건에 해당되지 않는다면 이웃 노드로 이동하는 비용을 갱신.
            costs[neighbor] = cost
            # 탐색 대상 노드에 이웃 노드 추가.
            queue.append(neighbor)
    
    # 문제에서 요구하는 비용을 만족하는 노드의 갯수 반환.
    return len([cost for cost in costs if cost <= K])

위에서 언급한 다익스트라 알고리즘과는 조금 다르게 방문한 노드를 따로 기억하진 않았다. 그러나 [i][j]+[j][k]와 [i][k]를 비교한다는 느낌으로 알고리즘을 구축하고 문제에서 요구하는 비용의 한계도 조건에 추가하는 방식으로 구현한다는 것을 알 수 있었다.

기본적인 출처는 언급했듯이 이곳이다. 내가 스스로 구현한 코드가 아닐지라도 많은 도움이 되는 경험이었다.

얕은 복사, 깊은 복사

위 코드에서 특이한 점은 노드 간 이동 비용을 저장하는 fees 2차원 배열 코드다. 이는 파이썬에서도 얕은 복사, 깊은 복사가 일어나기 때문인데 원래는 다음처럼 작성했었다.

fees = [[100001] * (N+1)] * (N+1)

이는 [100001] * (N+1)로 생성한 리스트 객체를 다시 N+1개 만큼 생성해서 리스트로 저장한다. 이 경우 리스트 안의 리스트 구조를 띄게 되는데 내부의 리스트는 100001이라는 정수값이 N+1개 복사된 것이기 때문에 별 문제가 없지만 외부 리스트의 경우 모든 요소들이 같은 객체를 가리키는 문제가 발생한다.

>>> a=[0]*5
>>> a
[0, 0, 0, 0, 0]
>>> a[1]=12345
>>> a
[0, 12345, 0, 0, 0]

예를 들어 위처럼 정수값을 곱셈 연산자로 여러개 생성한 경우 각각의 요소는 원시 타입이기 때문에 한 요소에 변경이 일어나도 다른 요소에 반영되지 않는다.

>>> b=[[0]*5]*5
>>> pprint(b)
[[0, 0, 0, 0, 0],
 [0, 0, 0, 0, 0],
 [0, 0, 0, 0, 0],
 [0, 0, 0, 0, 0],
 [0, 0, 0, 0, 0]]
>>> b[0][1]=12345
>>> pprint(b)
[[0, 12345, 0, 0, 0],
 [0, 12345, 0, 0, 0],
 [0, 12345, 0, 0, 0],
 [0, 12345, 0, 0, 0],
 [0, 12345, 0, 0, 0]]
>>>

그러나 위처럼 리스트를 다시 여러개 생성한 경우 얕은 복사가 일어나기 때문에 한 요소가 변경되면 다른 요소까지 같이 변경된다.

>>> id(b[0])
2391005880512
>>> id(b[1])
2391005880512
>>> id(b[2])
2391005880512
>>> id(b[3])
2391005880512
>>> id(b[4])
2391005880512

이는 리스트의 각 요소가 전부 동일한 요소를 가리키고 있기 때문인데 실제로 확인해보면 전부 동일한 id 값을 갖는 것을 볼 수 있다. 그렇기 때문에 다음처럼 수동으로 별도의 리스트를 생성해줘야 한다.

b = []
for _ in range(5):
    b.append([0]*5)

이 경우 외부 리스트의 각 요소는 서로 다른 요소기 때문에 이전처럼 서로 간섭하지 않는 것을 볼 수 있다

>>> pprint(b)
[[0, 0, 0, 0, 0],
 [0, 0, 0, 0, 0],
 [0, 0, 0, 0, 0],
 [0, 0, 0, 0, 0],
 [0, 0, 0, 0, 0]]
>>> b[0][1]=12345
>>> pprint(b)
[[0, 12345, 0, 0, 0],
 [0, 0, 0, 0, 0],
 [0, 0, 0, 0, 0],
 [0, 0, 0, 0, 0],
 [0, 0, 0, 0, 0]]
>>> id(b[0])
2391005901440
>>> id(b[1])
2391007229696
>>> id(b[2])
2391007229632
>>> id(b[3])
2391007230336
>>> id(b[4])
2391007230080