설명
LeetCode의 Cheapest Flights Within K Stops 문제다.
이전 다익스트라 문제와 거의 동일한데 방향성 가중치 그래프로 나타낸 항공로에서 제한된 만큼 환승하고 목적지에 도달할 수 있는 최단 거리를 계산하는 문제다.
일반적인 다익스트라 문제와 조금 다른점은 환승, 즉 이동할 수 있는 노드 갯수가 제한되어 있다는 것이다.
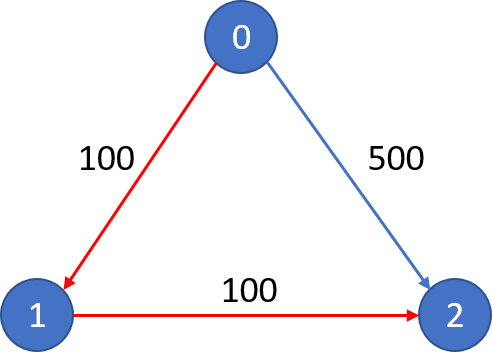 예를 들어 위와 같은 항공로가 있을 때 0번 공항에서 환승을 한번도 하지 않고 2번 공항에 도착하는 최단 거리는 얼마나 될까? 이 경우 0번 공항에서 2번 공항으로 가는 500짜리 경로를 이용할 수 밖에 없다.
예를 들어 위와 같은 항공로가 있을 때 0번 공항에서 환승을 한번도 하지 않고 2번 공항에 도착하는 최단 거리는 얼마나 될까? 이 경우 0번 공항에서 2번 공항으로 가는 500짜리 경로를 이용할 수 밖에 없다.
만약 환승을 한 번 허용한다면 0번, 1번, 2번 공항 순으로 이동하여 100 + 100 짜리 경로를 이용할 수 있다.
풀이
Dijkstra #1(실패)
첫번째로 시도한 풀이는 다익스트라 알고리즘을 다음처럼 변형하여 구현했다.
- 비용, 노드, 환승에 사용한 공항의 갯수를 우선순위 큐에 삽입한다.
- 현재까지 방문한 공항의 갯수가 환승 제한을 초과하면 탐색하지 않는다.
- 현재까지 누적된 비용이 기존에 계산된 비용보다 크다면 탐색하지 않는다.
특히 마지막 조건은 나름대로 최적화를 위해 넣었다고 생각했는데 이는 다음과 같은 반례에 막히고 말았다.
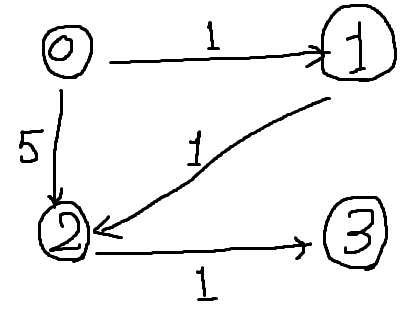 위의 그래프에서 0번 공항에서 3번 공항까지 한 번만 환승해서 도달해야 한다고 할 때 최적의 경로는 5 + 1 = 6이다. 1번 공항을 거쳐가면 1 + 1 + 1 = 3의 경로로 더 효율적이겠지만 한 번만 환승해야 한다는 제한이 있기 때문에 2번 공항으로 돌아갈 수밖에 없다.
위의 그래프에서 0번 공항에서 3번 공항까지 한 번만 환승해서 도달해야 한다고 할 때 최적의 경로는 5 + 1 = 6이다. 1번 공항을 거쳐가면 1 + 1 + 1 = 3의 경로로 더 효율적이겠지만 한 번만 환승해야 한다는 제한이 있기 때문에 2번 공항으로 돌아갈 수밖에 없다.
그런데 "누적된 비용이 기존에 계산된 비용보다 크다면 탐색하지 않는다"는 조건이 이 상황에서 문제가 되는 것이다. 왜냐면 다익스트라 알고리즘으로 탐색 시 0번 공항에서 1번 공항으로 가는 경로가 제일 비용이 낮기 때문에 1번 공항을 먼저 탐색하고 이후 2번 공항도 탐색하게 된다. 그리고 3번 공항까지는 환승 제한에 걸려서 탐색하지 못하지만 결과적으로 0번 공항에서 2번 공항까지 최단거리가 1 + 1 = 2로 확정지어진다.
그리고 큐에 남아있는 비용 5의 0번 공항에서 2번 공항으로 가는 경로를 탐색하게 될 때 위에서 탐색된 비용 2에 비교해서 현재 경로가 더 비효율적이기 때문에 더이상 탐색하지 않는다. 여기까지는 일반적인 다익스트라 문제였다면 옳은 방법이다.
하지만 고려해야 할 점은 이 문제에는 환승 제한이 있다는 것이다. 0번 공항에서 1번 공항으로 가는 경로는 2번 공항까지는 비용 2로 이동할 수 있어도 3번 공항까지는 이동할 수 없다. 문제에서는 어찌됐든 3번 공항까지 이동해야 하기 때문에 이 경로는 사실상 무용지물인 것이다.
이를 구현했던 코드는 다음과 같다.
import collections
import heapq
class Solution:
def findCheapestPrice(self, n: int, flights: List[List[int]], src: int, dst: int, K: int) -> int:
# 노드 간 연결관계, 가중치, 초기 노드에서 다른 노드까지의 거리.
graph = collections.defaultdict(list)
costs = [[10001]*(n+1) for _ in range(n+1)]
terminalCosts = [1000001]*(n+1)
# 그래프 초기화
for flight in flights:
departure, destination, cost = flight
graph[departure].append(destination)
costs[departure][destination] = cost
# 우선순위 큐에 (비용, 노드, 환승 횟수) 튜플 삽입.
queue = [(0, src, 0)]
while queue:
# 가장 적은 비용의 노드 추출.
cost, node, stop = heapq.heappop(queue)
# 환승 횟수를 초과했거나 기존보다 효율적이지 않은 경로 무시.
if stop > K+1 or terminalCosts[node] <= cost:
continue
# 현재 노드의 이웃 노드를 큐에 삽입.
for neighbor in graph[node]:
heapq.heappush(queue, (cost + costs[node][neighbor], neighbor, stop+1))
# 현재 노드까지의 이동 거리 갱신.
terminalCosts[node] = min(cost, terminalCosts[node])
# 목적지 노드까지 경로가 파악됐다면 거리값 반환.
return -1 if terminalCosts[dst] > 1000000 else terminalCosts[dst]Dijkstra #2(96 ms)
그럼 어떻게 해야 위의 문제를 해결할 수 있을까? 답은 이동 거리가 아닌 환승 횟수로 탐색 중단 여부를 확인하는 것이다. 위의 그래프에서도 0번 공항에서 2번 공항로 이동할 때 비용(5 > 1+1)이 아닌 환승 횟수(1 < 2)로 비교한다면 유효한 경로를 따라서 최단거리를 탐색할 수 있다.
하지만 그냥 구현했을 때는 시간초과가 발생했는데 알고리즘의 한계인지 구현이 잘못된 것인지 파악하지 못했다. 대신 현재 탐색한 노드는 최단거리를 가지게 된다라는 다익스트라 알고리즘의 특성을 활용하여 탐색 중 목적지 노드에 도달했을 때 바로 탐색을 종료하도록 구현하여 불필요한 연산을 무시할 수 있다.
import collections
import heapq
class Solution:
def findCheapestPrice(self, n: int, flights: List[List[int]], src: int, dst: int, K: int) -> int:
# 노드 간 연결관계, 가중치, 시작 노드와 다른 노드간 거리.
graph = collections.defaultdict(list)
costs = [[10001]*(n) for _ in range(n)]
terminalCosts = [1000001]*(n)
# 그래프 초기화.
for flight in flights:
departure, destination, cost = flight
graph[departure].append(destination)
costs[departure][destination] = cost
# src 노드부터 탐색 시작.
queue = [(0, src, 0)]
while queue:
# 제일 낮은 비용의 경로부터 탐색.
cost, node, stop = heapq.heappop(queue)
# 현재 방문한 노드의 거리값 갱신.
terminalCosts[node] = min(cost, terminalCosts[node])
# 문제에서 요구한 환승 횟수를 초과하게 되는 경우 탐색 종료.
if stop > K:
continue
# 현재 노드가 목적지 노드라면 탐색 종료.
if node == dst:
return terminalCosts[node]
# 현재 노드의 이웃 노드를 증가된 환승 횟수와 함께 탐색 대기열에 추가.
for neighbor in graph[node]:
calculatedCost = cost + costs[node][neighbor]
heapq.heappush(queue, (calculatedCost, neighbor, stop+1))
# 목적지 노드까지 도달할 수 있다면 최단거리 반환.
return -1 if terminalCosts[dst] > 1000000 else terminalCosts[dst]그런데 이 문제의 또다른 특징은 최단거리를 구하고자 하는 경로(시작 노드, 도착 노드)가 명확히 지정되어 있다는 것이다. 이 경우 terminalCosts 배열처럼 시작 노드부터 다른 모든 노드까지의 길이를 저장하고 있을 필요가 없다. 그래서 위의 코드를 좀 더 간략화하면 다음과 같다.
import collections
import heapq
class Solution:
def findCheapestPrice(self, n: int, flights: List[List[int]], src: int, dst: int, K: int) -> int:
# 노드 간 연결관계, 가중치.
graph = collections.defaultdict(list)
costs = [[10001]*(n) for _ in range(n)]
# 그래프 초기화.
for flight in flights:
departure, destination, cost = flight
graph[departure].append(destination)
costs[departure][destination] = cost
# src 노드부터 탐색 시작.
queue = [(0, src, 0)]
while queue:
# 제일 적은 비용의 탐색 경로 추출.
cost, node, stop = heapq.heappop(queue)
# 현재 경로가 목적지 노드라면 최단거리 반환.
if node == dst:
return cost
# 환승 횟수를 초과하게 된다면 더이상 탐색하지 않음.
if stop > K:
continue
# 현재 노드의 이웃 노드를 탐색 큐에 삽입.
for neighbor in graph[node]:
calculatedCost = cost + costs[node][neighbor]
heapq.heappush(queue, (calculatedCost, neighbor, stop+1))
# 목적지 노드의 최단거리를 발견하지 못했다면 -1 반환.
return -1시간 차이는 크지 않았지만 불필요한 변수가 없다는 점에서 더 간결하고 좋은 코드라고 생각한다.
후기
환승 횟수로 결정하는 부분까진 구현했지만 시간 초과 문제에서 고전하고 있었는데 현재 경로가 목적지 노드일 경우 바로 반환한다는 로직 덕분에 풀 수 있었다. 이는 처음 찾은 경로가 최단경로라는 다익스트라 알고리즘의 핵심 원리를 잘 알고 있었다면 생각해낼 수 있었던 부분이 아닐까 싶다. 어제 그렇게 나름대로 공부했지만 아직도 부족하다는 것을 확연히 느낄 수 있었다.
