rbTree 이론

레드블랙 트리

• 이진 검색트리로써 각 노드당 한 비트의 추가기억 공간을 가짐.
• 이 공간에 노드의 색깔을 나타내는데 red이거나 흑색이 됨
• 루트에서 리프까지의 경로에 나타내는 노드의 색깔을 제한함으로써 경로 중 어떠한 것도 다른 경로보다 2배이상 길지 않음을 보장함으로써 근사적으로 균형을 이룬 트리가 됨.
• 각 노드는 color, key, left, right, parent 등의 필드값을 가짐
• 한 노드의 부모 또는 자식 노드가 없으면 그에 대응하는 노드의 포인터 필드는 NIL값으로 채워짐
• 이진검색 트리에서 노드가 NIL값을 가지면 → 리프노드, 키를 가진 정상적인 노드 → 트리의 내부노드

레드블랙 트리의 특성

1. 모든 노드는 red이거나 black이다.
2. 루트는 black이다.
3. 모든 리프(NiL)노드는 black이다.
4. 노드가 red이면 그 노드의 자식은 모두 black이다.
   • red가 연속적으로 존재할 수 없다는 의미
5. 각 노드로부터 그 노드의 자손인 리프로 가는 경로들은 모두 같은 수의 black 노드를 포함한다.
   • 자기 자신은 카운트에서 제외
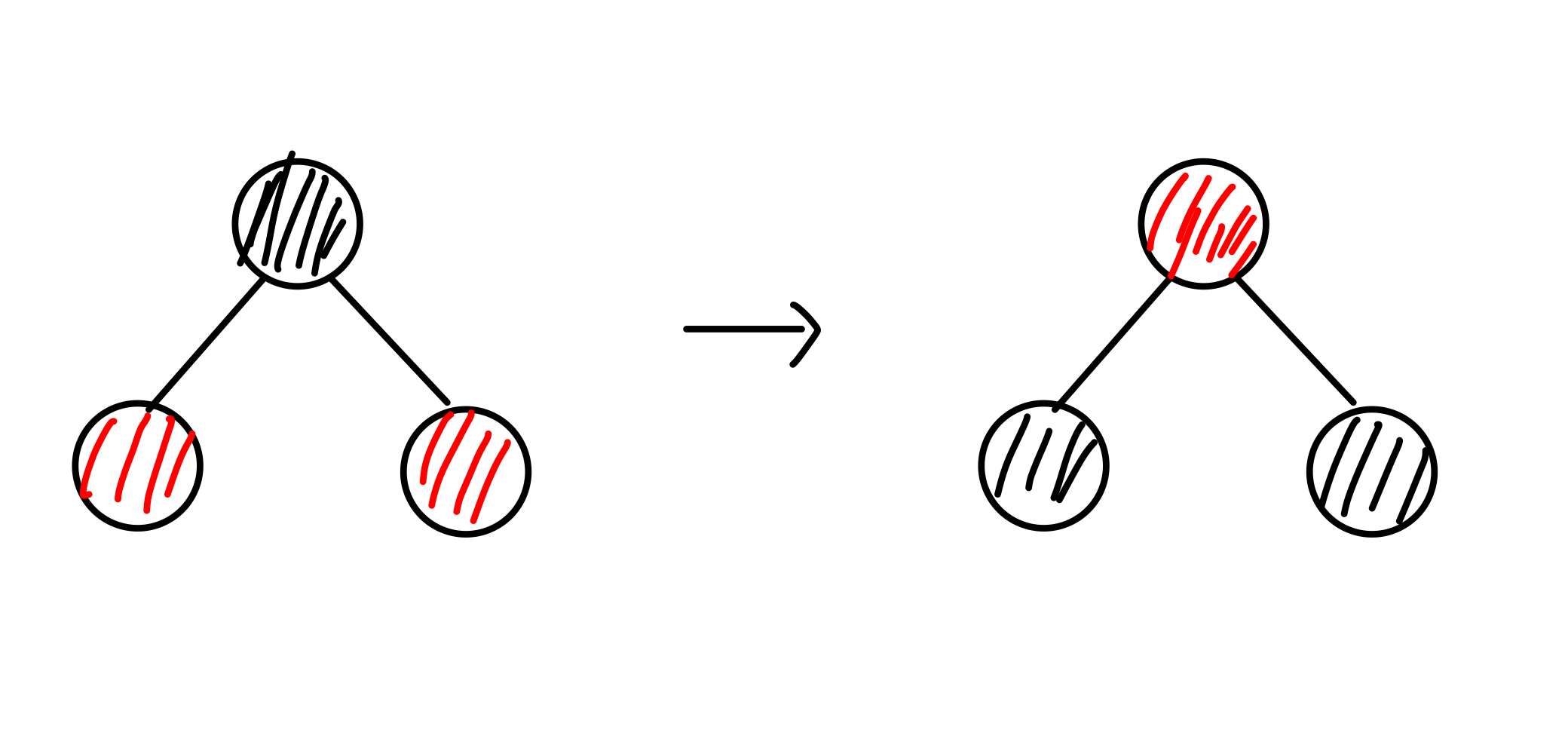
   • rbtree가 5번 속성을 만족하고 두 자녀가 같은 색을 가질 때 부모와 두 자녀의 색을 바꿔줘도 5번속성은 여전히 만족한다.
     

회전

노드를 삭제하거나 삽입할 때 트리를 수정하기 때문에 레드블랙 트리의 특성을 위반할 수 있다.

이러한 특성을 복구하기 위해 트리 내의 일부 노드들의 색깔과 포인터를 변경해야 한다.

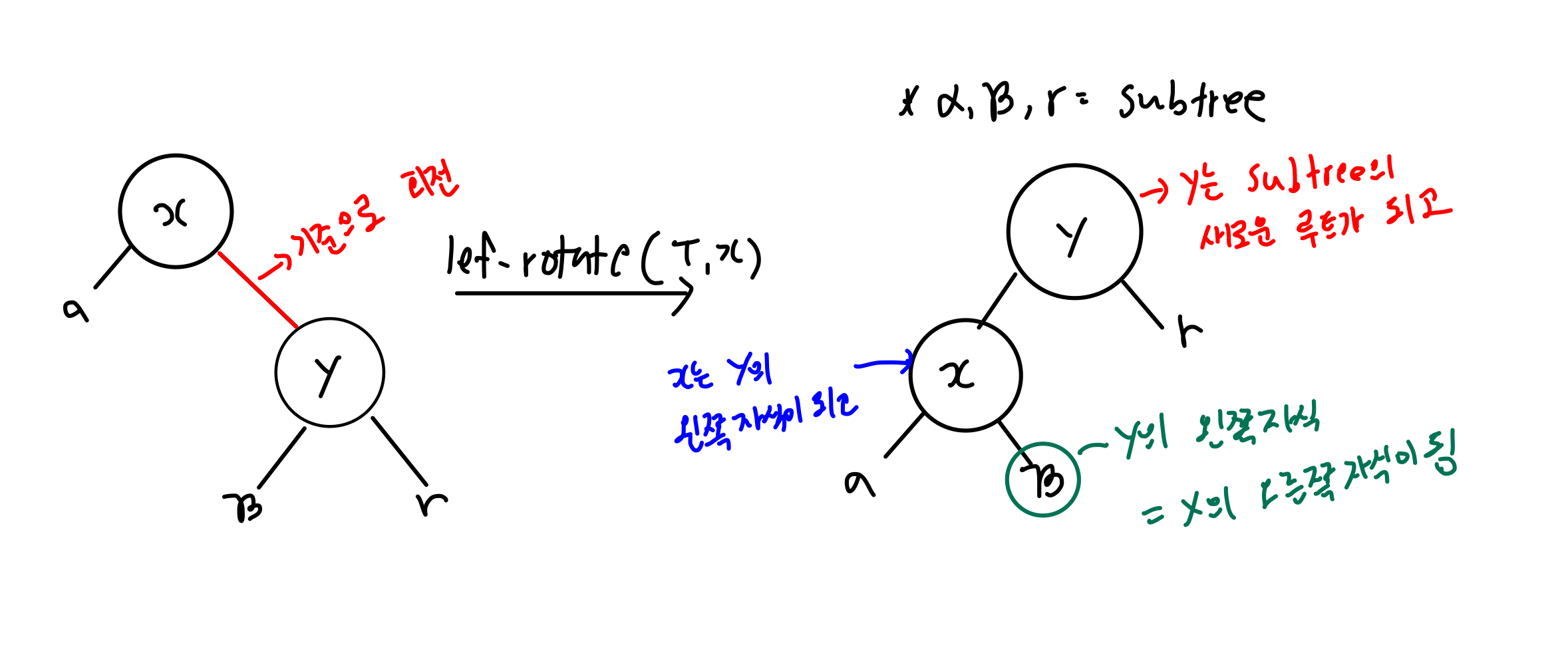
1. 좌회전(Left Rotate)

노드 x에 대해서 좌회전을 할 때 오른쪽 자식은 NIL이 아니라고 가정

1. 노드 x와 노드 y가 연결된 축을 기준으로 회전

2. 노드 y는 서브트리의 새로운 루트가 됨

3. 노드 x는 노드 y의 왼쪽 자식이 됨

4. y의 왼쪽 자식이였던 $b$는 노드 x의 오른쪽 자식이 됨

   sudo code

   1. y를 x의 오른쪽 노드라고 변수에 담기

   2. y의 왼쪽 서브트리를 x의 오른쪽으로 옮김

   3. 옮긴 트리의 부모도 x로 지정

   4. x의 부모를 y와 연결

      • x의 부모가 없으면 y를 루트로 지정
      • x가 x 부모의 왼쪽 서브트리이면 x의 부모의 왼쪽과 y를 연결
      • x가 x 부모의 오른쪽 서브트리라면 x의 부모의 오른쪽과 y를 연결

      

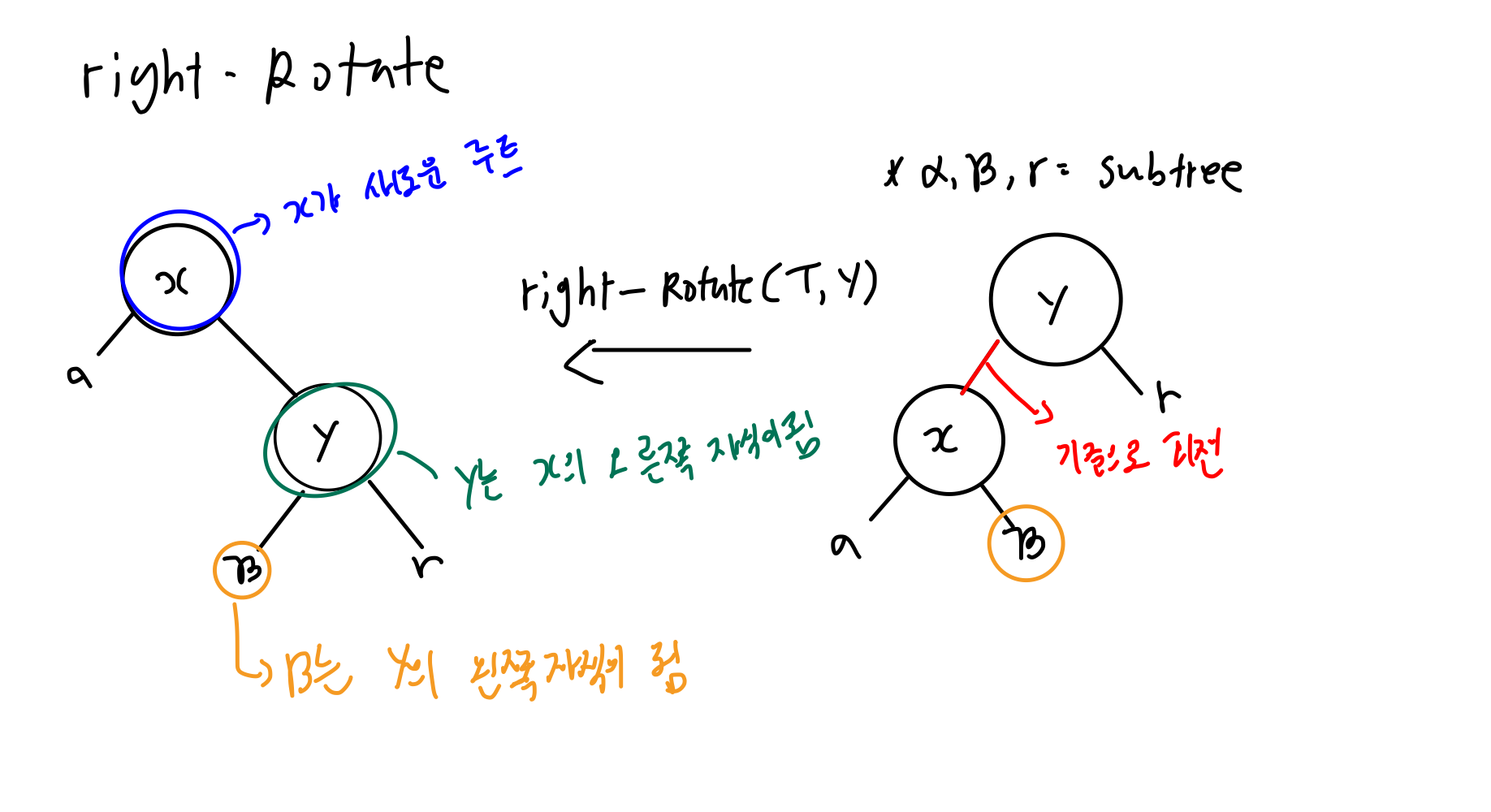
2. 우회전(Right Rotate)

1. 노드 x와 노드 y가 연결된 축을 기준으로 회전

2. 노드 x가 새로운 서브트리의 루트가 됨

3. 노드 y는 노드 x의 오른쪽 자식이 됨

4. 노드 x의 오른쪽 자식이였던 $b$는 노드 y의 왼쪽 자식이 됨

   sudo code

   1. x를 y의 왼쪽 노드라고 변수에 담기

   2. y의 왼쪽 서브트리를 x의 오른쪽으로 옮김

   3. 옮긴 트리의 부모도 x로 지정

   4. x의 부모를 y와 연결

      • x의 부모가 없으면 y를 루트로 지정
      • x가 x 부모의 왼쪽 서브트리이면 x의 부모의 왼쪽과 y를 연결
      • x가 x 부모의 오른쪽 서브트리라면 x의 부모의 오른쪽과 y를 연결

      

언제 회전을 하는가?

4번 속성을 위반했을 때

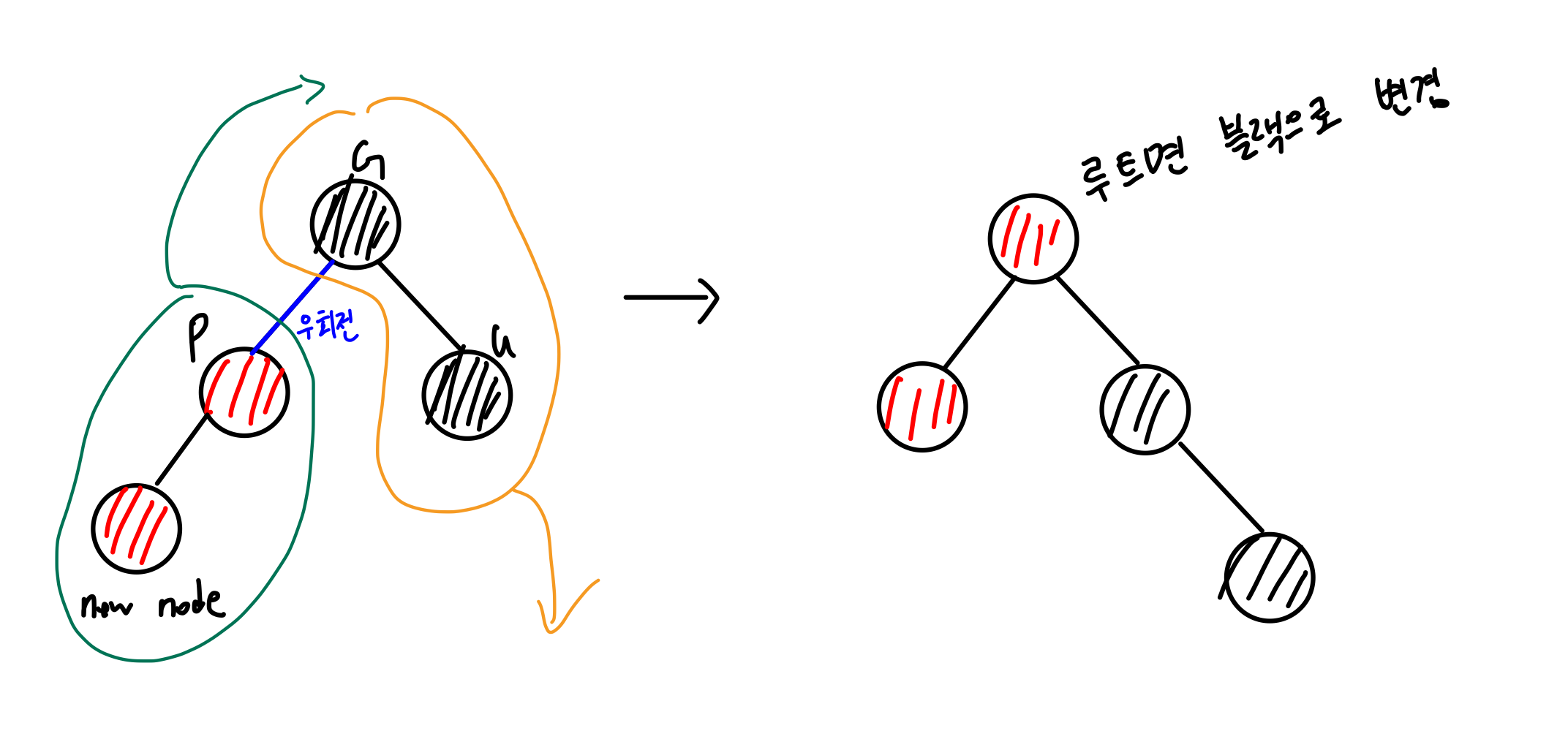
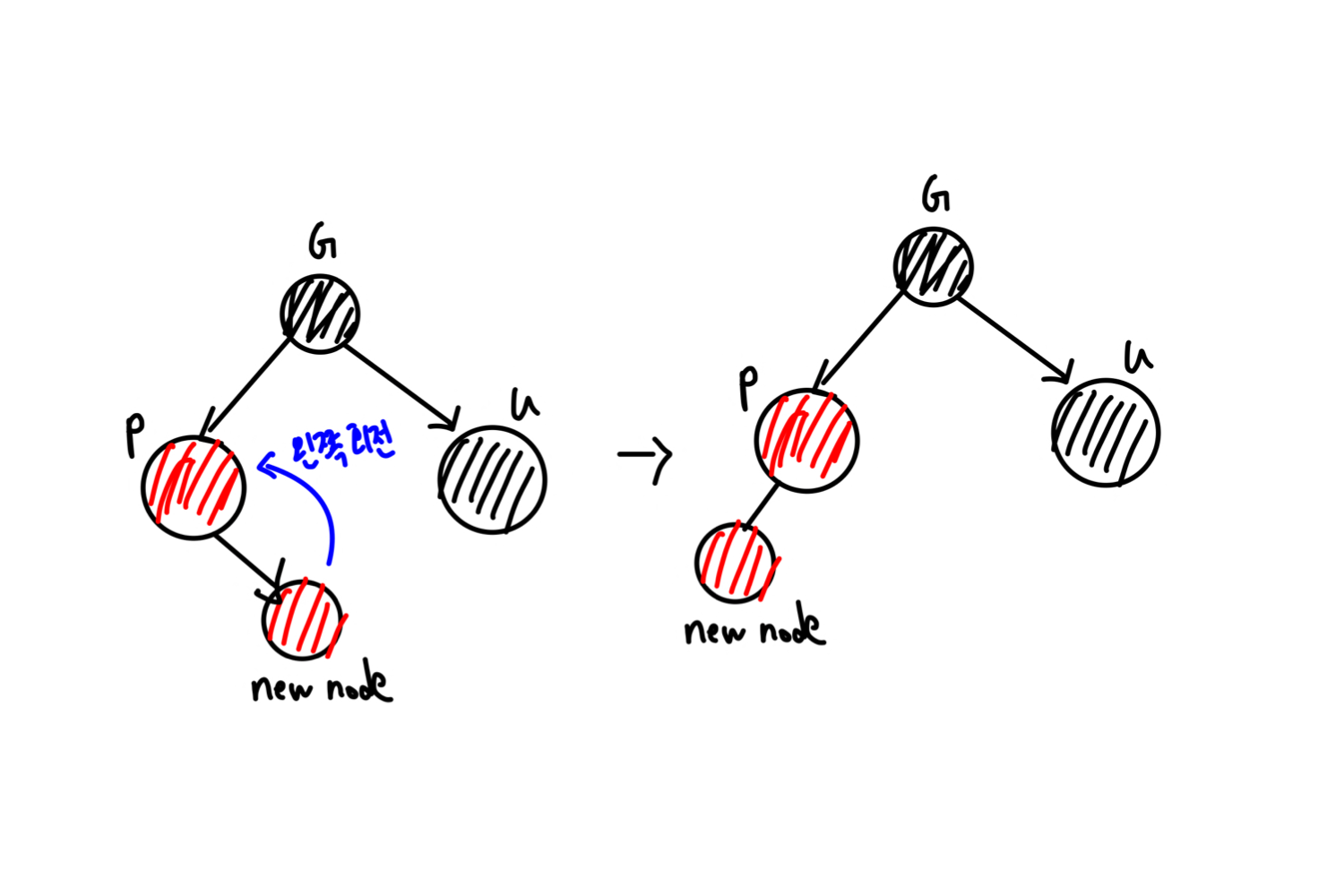
• case 3: 삽입된 새로운 red 노드가 부모의 왼쪽 자녀 & 부모도 red이고 할아버지의 왼쪽 자녀 & 삼촌은 black인 경우 → 할아버지 노드를 기준으로 오른쪽 회전한다.

  • G(할아버지), P(부모), U(삼촌), new node(새로운 노드)

  • case 3에서 왼쪽과 오른쪽을 변경해도 성립한다. (왼쪽 → 오른쪽) / (오른쪽 → 왼쪽)

    

• case 2: 삽입된 red 노드가 부모의 오른쪽 자녀 & 부모도 red이면서 할아버지의 왼쪽 자녀 & 삼촌이 black → 부모를 기준으로 왼쪽 회전한 뒤 case 3 방식으로 해결

  • 할아버지 노드와 부모노드와 삽입한 새로운 노드가 꺾인 형태이면 회전을 통해 일직선으로
    펴준다음에 case 3방식으로 해결

  • Case3와 마찬가지로 왼쪽과 오른쪽 방향을 바꿔도 성립

    

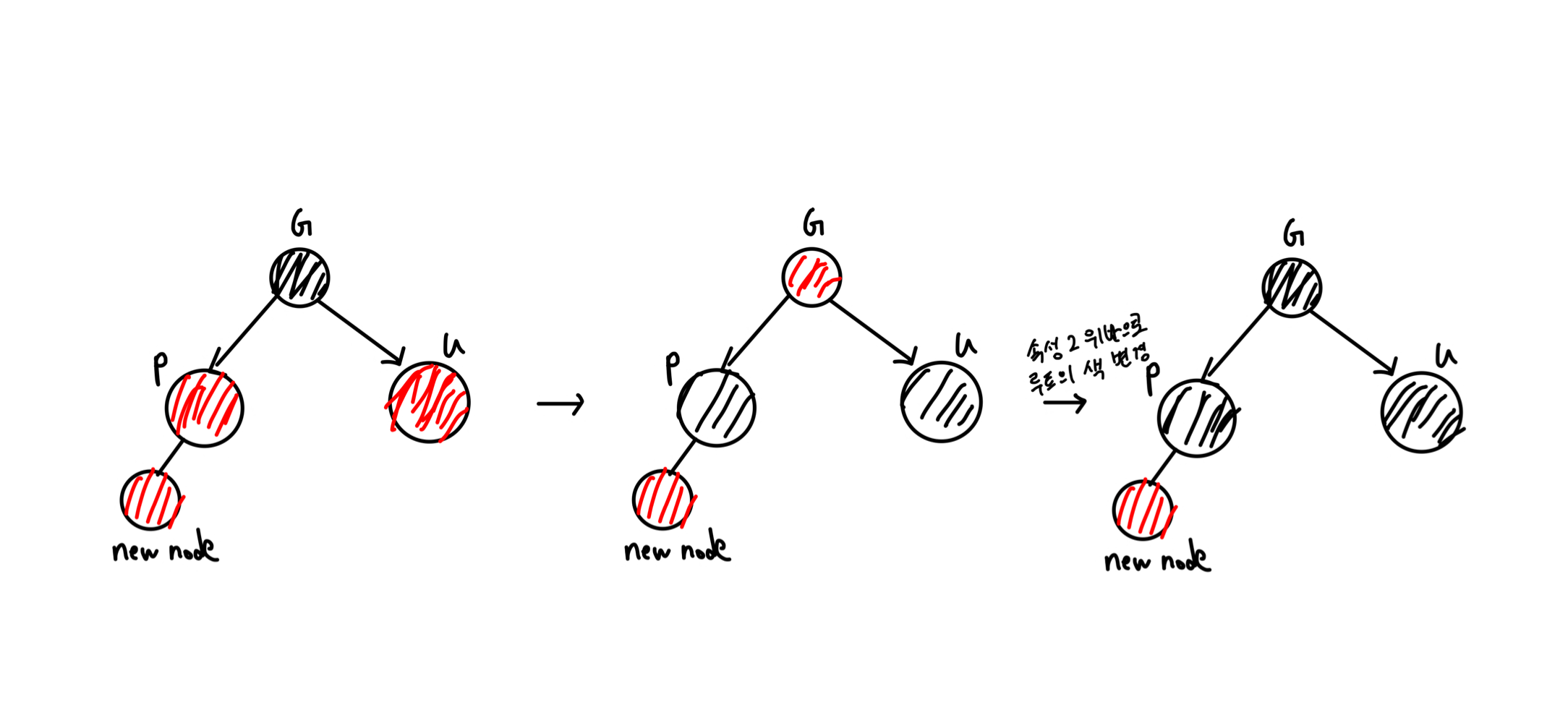
• case 1: 삽입된 red 노드의 부모도 red & 삼촌도 red → 부모와 삼촌을 black으로 바꾸고 할아버지를 Red로 바꾼 뒤 할아버지에서 속성을 다시 확인한다.

삽입

삽입 전 rb트리 속성을 만족한 상태

순서

1. 삽입방식은 일반적인 bst와 동일
2. 삽입 후 rb트리 위반 여부 확인
3. 위반했다면 재조정
   • 위에서 설명한 회전을 통해 재조정

삽입하는 노드의 색은 항상 red
왜? → 삽입 후에도 5번 속성을 만족하기 위해서

삭제

과정

1. 삭제 전 rb 트리 속성을 만족한 상태
2. 삭제 방식은 일반적인 bst와 동일
3. 삭제 후 rb 트리 속성 위반 여부를 확인
   • 위반했다면 재조정

속성 위반 여부를 확인하는 방법은 삭제되는 색을 통해

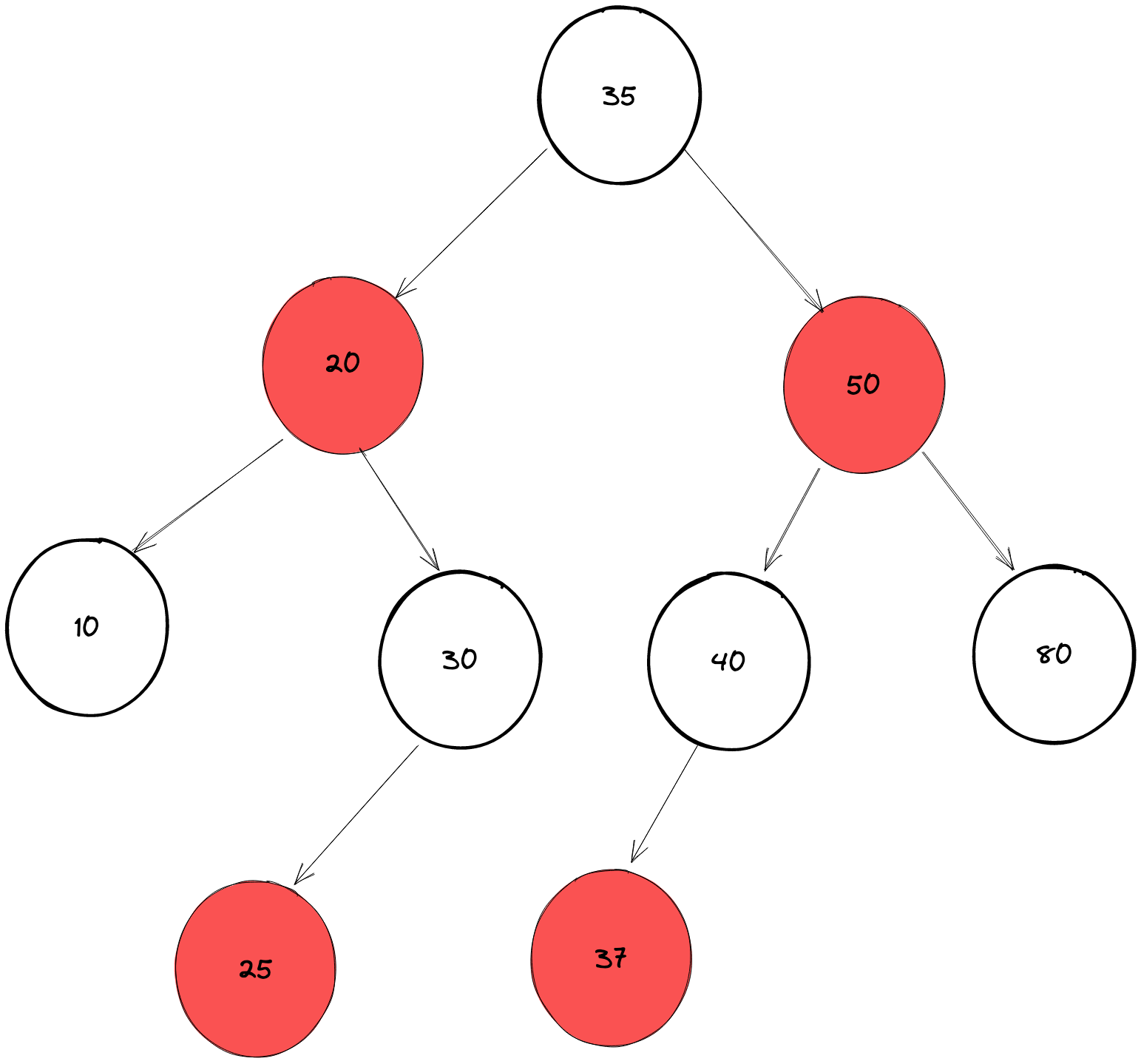
(두 경우 다 유효한 값을 가지는 자녀를 의미)

1. 삭제하려는 노드의 자녀가 없거나 하나라면

   → 삭제되는 색은 삭제되는 노드의 색

   • 25 삭제 → red 삭제
   • 80 삭제 → black 삭제

2. 삭제하려는 노드의 자녀가 둘이라면

   → 삭제되는 색은 삭제되는 노드의 successor의 색

   successor: 삭제할려는 노드의 오른쪽 서브트리에서 가장 작은 값

   • 20 삭제 → successor 25 → red 삭제
   • 35 삭제 → successor 37 → red 삭제
   • 50 삭제 → successor 80 → black 삭제

속성 위반 여부 확인

삭제되는 색이 red라면 어떠한 속성도 위반하지 않는다.

삭제되는 색이 black이라면 2,4,5번 속성을 위반할 수 있다.

• 2번 속성을 위반햇을 경우 루트 노드를 black으로 변경하면 됨
• black노드를 삭제한 경우 대부분 5번 속성을 위반하게 됨 →
  • 빠르게 5번속성을 만족시키기 위해 삭제된 노드를 대체한 노드에 extra black 속성을 부여한다.
  • extra black: 경로에서 black 수를 카운트 할 때 하나의 black으로 카운드 된다.
  • doubly black: extra black이 부여된 black 노드
  • red-and-black | extra black이 부여된 red 노드

해결방법

red-and-black일 경우: black으로 바꾸면 해결

doubly black일 경우: 4가지의 경우가 있음

→4가지로 분류된 기준은 doubly black의 형제의 색과 그 형제의 자녀들의 색임

• case 4: doubly black의 오른쪽 형제가 black & 그 형제의 오른쪽 자녀가 red
  
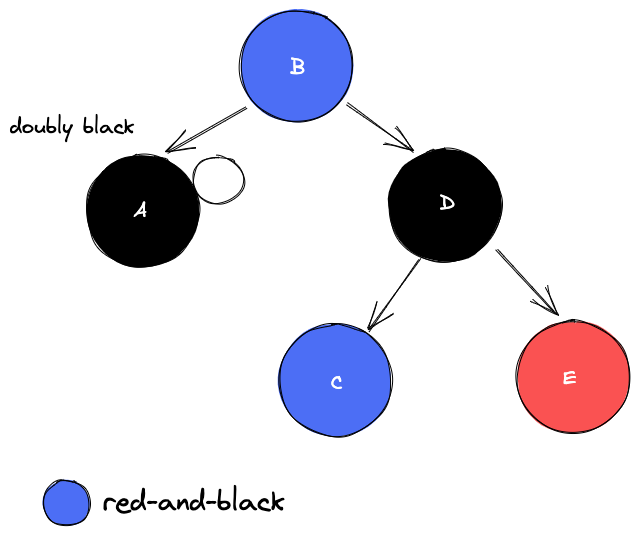
  → red를 doubly black 위로 옮기고 옮긴 red로 extra black을 전달해서 red-and-black으로 만들면 red-and-black을 black으로 바꿔서 해결

  red를 왼쪽으로 보내기 위해서는 d의 위치가 red가 되어야함
  

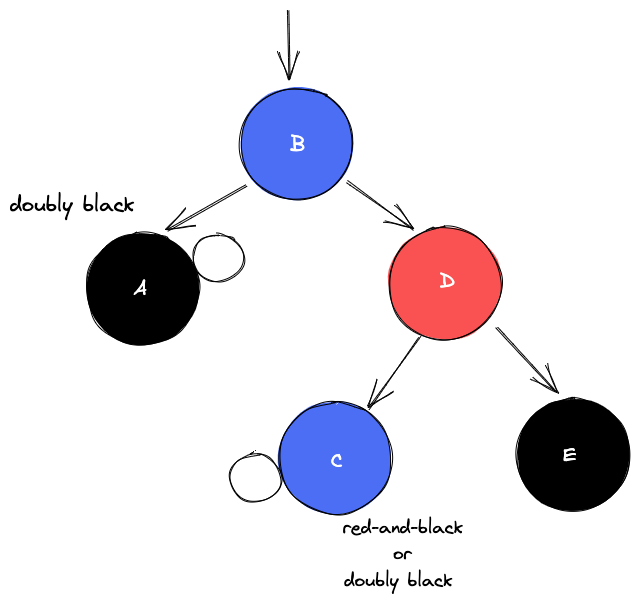
  red가 왼쪽으로 넘어갈 수 있도록 왼쪽으로 회전 전에 b와 d의 색을 바꿔준다.
  

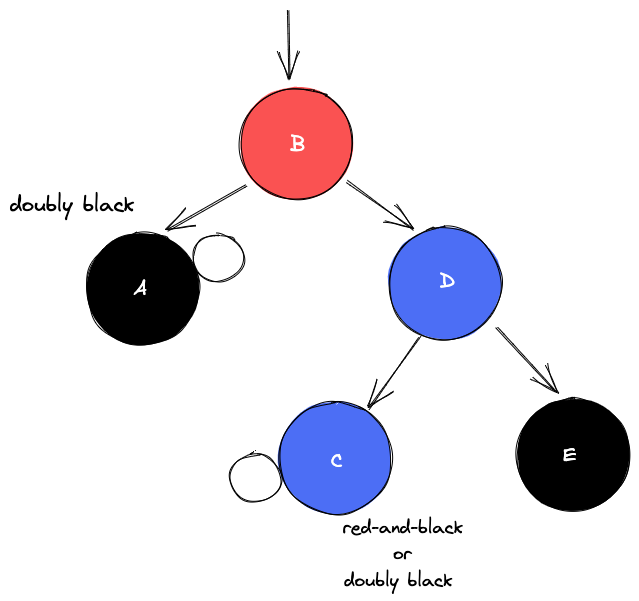
  B를 기준으로 왼쪽으로 회전한다.

  

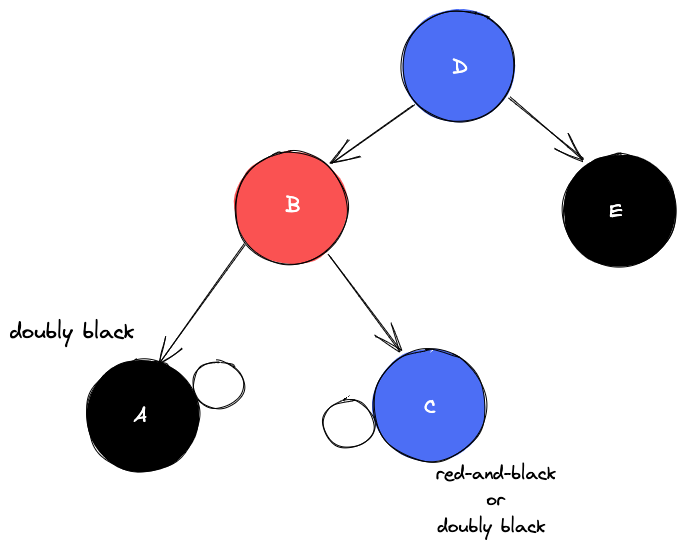
  A와 C의 extra black을 모아 부모로 전달해 B를 black으로 만들어 문제를 해결한다.

  

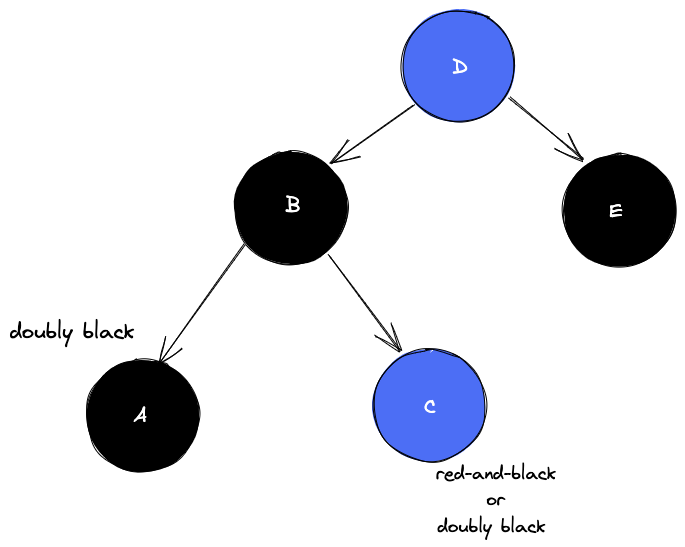
  결과론적으로

  • 오른쪽 형제(D)는 부모의 색으로

  • 오른쪽 형제의 오른쪽 자녀(E)는 black으로

  • 부모는 black으로 바꾼 후에 부모를 기준으로 왼쪽 회전하면 해결

    오른쪽 왼쪽을 바꿔도 성립

• case 3: doubly black의 오른쪽 형제가 black & 그 형제의 왼쪽 자녀가 red & 그 형제의 오른쪽 자녀가 black일 때

  

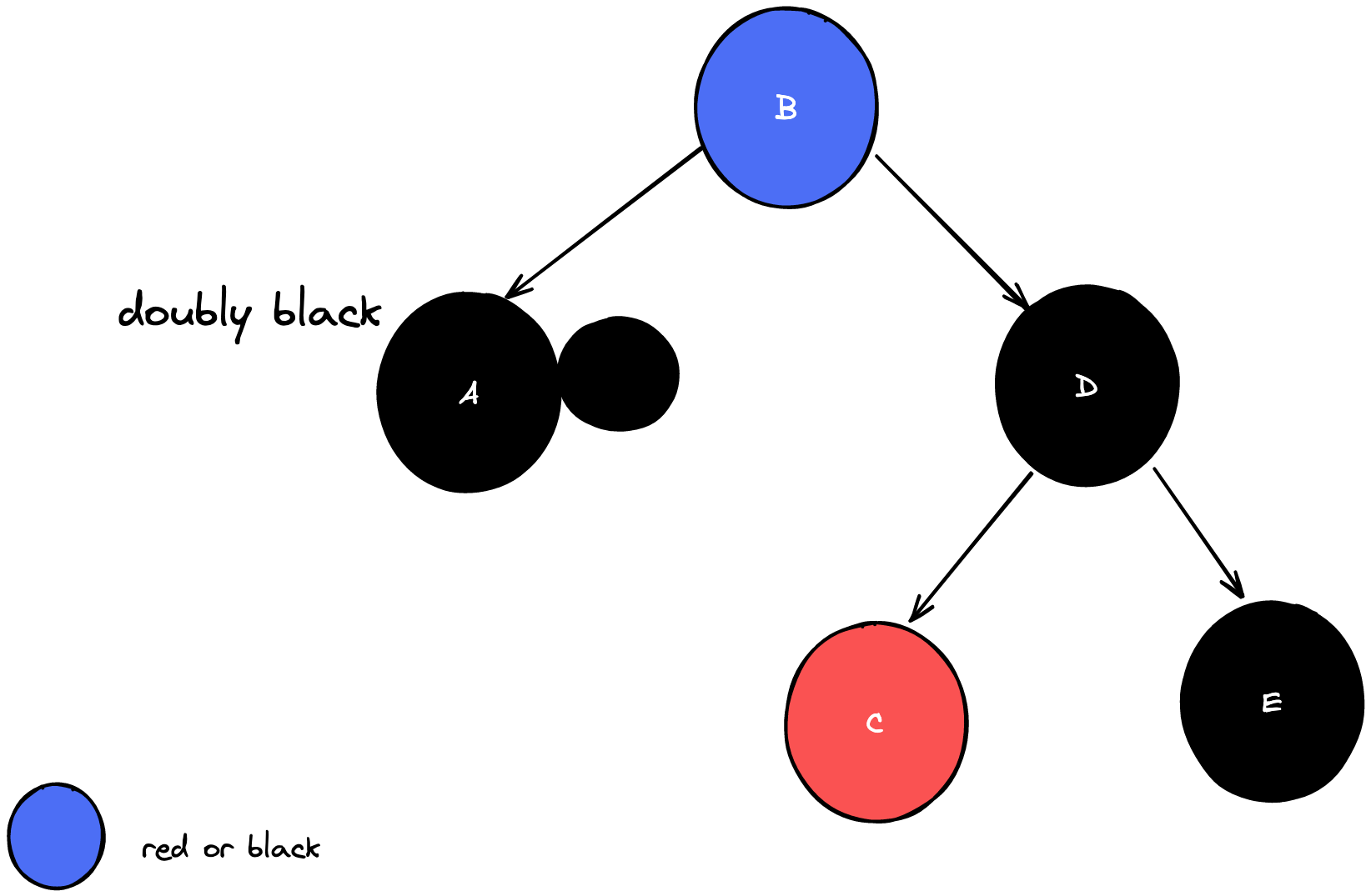
  → doubly black의 형제의 오른쪽 자녀가 red가 되게 만들어서 이후에 case 4를 적용하면 해결!

  E 위치에 red가 오게 만들려면 C와 D의 색을 바꾼 후 D를 기준으로 오른쪽 회전하면 된다.
  

• case 2: doubly black의 형제가 black & 그 형제의 두 자녀 모두 black

  

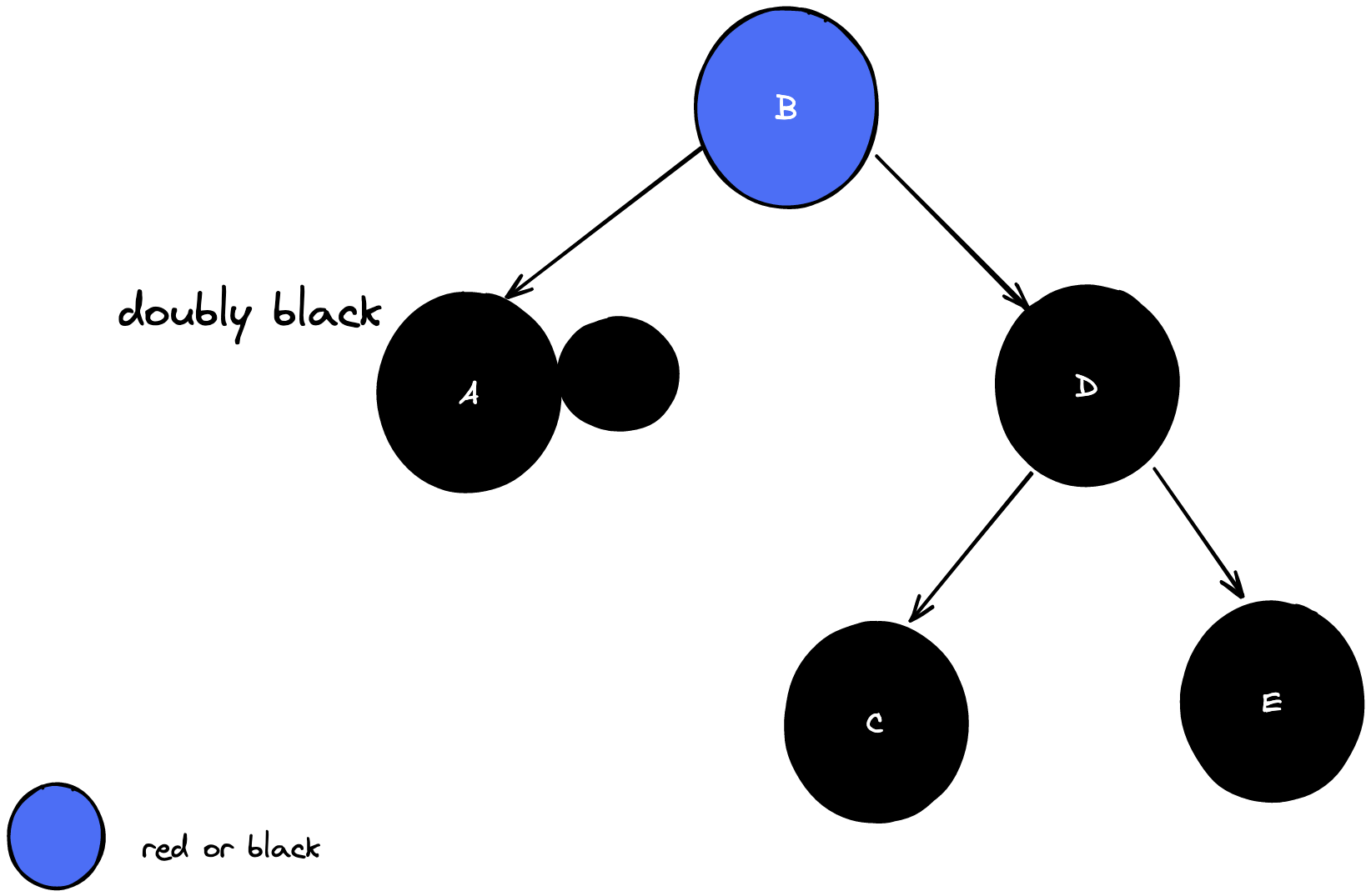
  doubly black과 그 형제의 black을 모아서 부모에게 전달 후 부모가 extra black을 해결하도록 위임

  1. B가 red-and-black이면 black으로 변경 후 끝
  2. B가 doubly black이면
     • B가 루트이면 black으로 바꿔서 해결
     • 아니라면 case 1,2,3,4 중 하나로 해결

• case 1: doubly black의 형제가 red일 때

  

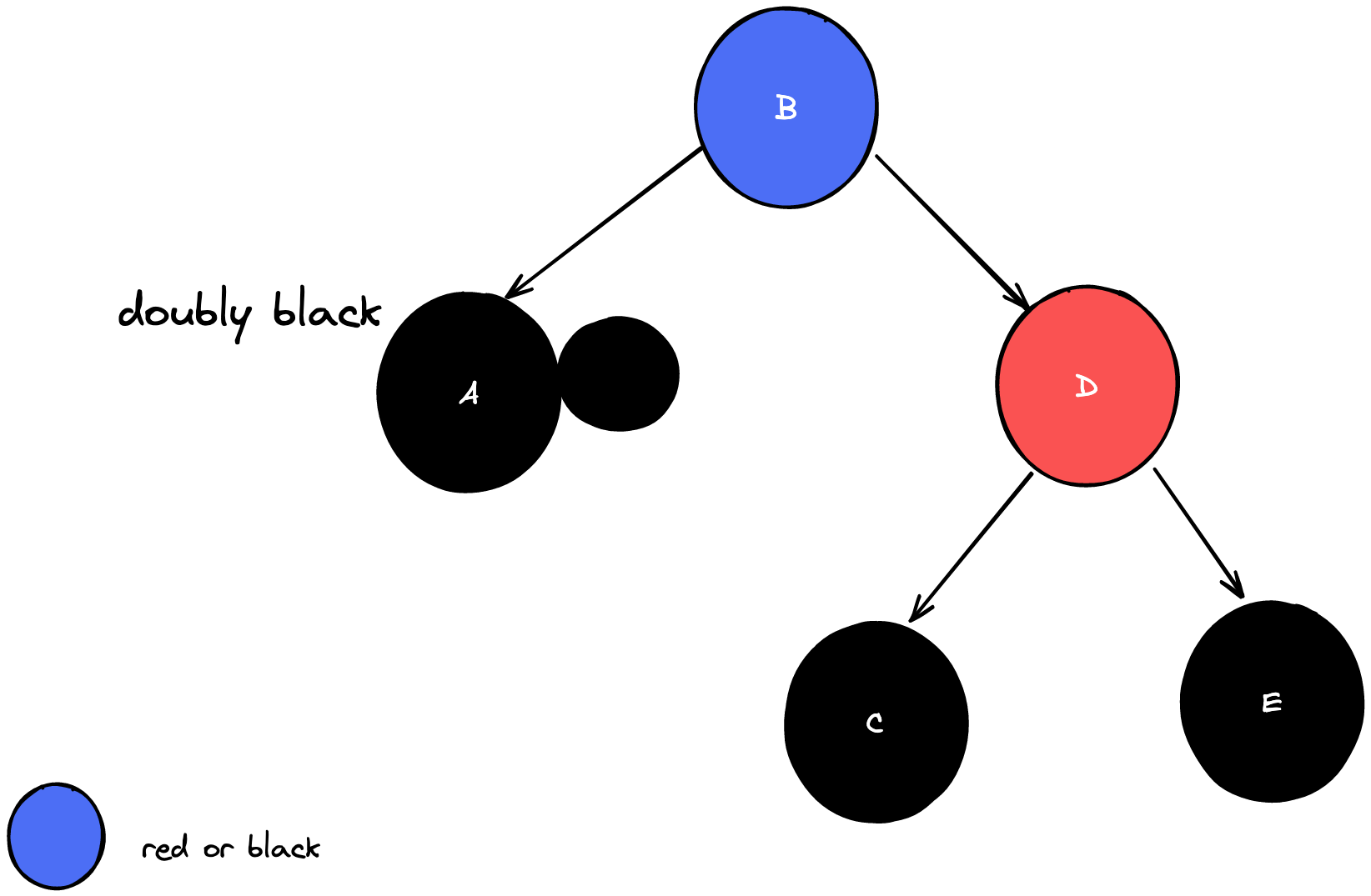
  부모와 형제의 색을 바꾸고 부모를 기준으로 왼쪽 회전한 뒤 doubly black을 기준으로 case 2,3,4 중 하나로 해결
  

reference

• introduction to algorithms
• red-black-tree Insert
• red-black-tree delete