[백준 Gold I] 외판원 순회 - 2098 파이썬

문제 설명

외판원 순회 문제는 영어로 Traveling Salesman problem (TSP) 라고 불리는 문제로 computer science 분야에서 가장 중요하게 취급되는 문제 중 하나이다. 여러 가지 변종 문제가 있으나, 여기서는 가장 일반적인 형태의 문제를 살펴보자.

1번부터 N번까지 번호가 매겨져 있는 도시들이 있고, 도시들 사이에는 길이 있다. (길이 없을 수도 있다) 이제 한 외판원이 어느 한 도시에서 출발해 N개의 도시를 모두 거쳐 다시 원래의 도시로 돌아오는 순회 여행 경로를 계획하려고 한다. 단, 한 번 갔던 도시로는 다시 갈 수 없다. (맨 마지막에 여행을 출발했던 도시로 돌아오는 것은 예외) 이런 여행 경로는 여러 가지가 있을 수 있는데, 가장 적은 비용을 들이는 여행 계획을 세우고자 한다.

각 도시간에 이동하는데 드는 비용은 행렬 W[i][j]형태로 주어진다. W[i][j]는 도시 i에서 도시 j로 가기 위한 비용을 나타낸다. 비용은 대칭적이지 않다. 즉, W[i][j] 는 W[j][i]와 다를 수 있다. 모든 도시간의 비용은 양의 정수이다. W[i][i]는 항상 0이다. 경우에 따라서 도시 i에서 도시 j로 갈 수 없는 경우도 있으며 이럴 경우 W[i][j]=0이라고 하자.

N과 비용 행렬이 주어졌을 때, 가장 적은 비용을 들이는 외판원의 순회 여행 경로를 구하는 프로그램을 작성하시오.

입력

첫째 줄에 도시의 수 N이 주어진다. (2 ≤ N ≤ 16) 다음 N개의 줄에는 비용 행렬이 주어진다. 각 행렬의 성분은 1,000,000 이하의 양의 정수이며, 갈 수 없는 경우는 0이 주어진다. W[i][j]는 도시 i에서 j로 가기 위한 비용을 나타낸다.

항상 순회할 수 있는 경우만 입력으로 주어진다.

출력

첫째 줄에 외판원의 순회에 필요한 최소 비용을 출력한다.

풀이

이 문제는 dp + dfs + 비트마스킹의 개념을 모두 알고 있어야 시간초과가 나지않고
통과가 되는 문제이다.

비트마스킹

이 문제를 풀기위해서는 비트마스킹을 이해해야한다.
이 문제의 경우 이진법을 사용해서 방문한 도시를 0과 1로 표시한다.

• 0b1인 경우 -> 도시 1을 방문
• 0b11인 경우 -> 도시 1과 2를 방문
• 0b 101인 경우 -> 도시 1과 3을 방문

코드의 경우 비트마스킹을 활용하여 모든 도시를 방문한 경우, 방문한 도시를 1로 만들 때, 방문한 도시인지 체크할 때도 사용한다.

1. 모든 도시를 방문했는지 체크하는 경우

   if route == (1 << (N - 1)) - 1

   여기서 N이 4라면 -1을 해서 3이 되고 1을 왼쪽으로 비트를 3만큼 옮긴다면 0b100이 되 8이 된다. 하지만 여기서 0b100은 도시 3만 방문한 경우를 의미하므로 -1을 해서 7로 만들어 주어 0b111이 되어 모든 도시를 방문했는지 체크할 수 있다.
   
   
2. 방문한 도시인지 체크하는 경우

   if route & (1 << j - 1):
           continue

   &연산자의 경우
   • 1 & 1 = 1
   • 0 & 1 = 0
     이를 활용하여 현재 방문한 도시인 route가 0b1이고 방문할려는 도시가 2인 경우
     2 - 1 = 1이고 1을 왼쪽으로 비트를 1만큼 옮기면 0b10이다.
   • 0b1 & 0b10 = 0이므로 방문을 안한 경우여서 continue하지 않고 방문한다.

3. 방문한 도시를 1로 만드는 경우

   solution(j, route | (1 << (j - 1)))

   '|'연산자의 경우 0과 1을 연산하면 1이된다. 이를 활용해 만약 route가 0b101이고 다음으로 방문할려는 도시가 2인 경우 0b101 | 0b10 = 0b111이 되어 도시 2를 비트마스킹을 활용하여 방문했다고 표시할 수 있다.

메모이제이션

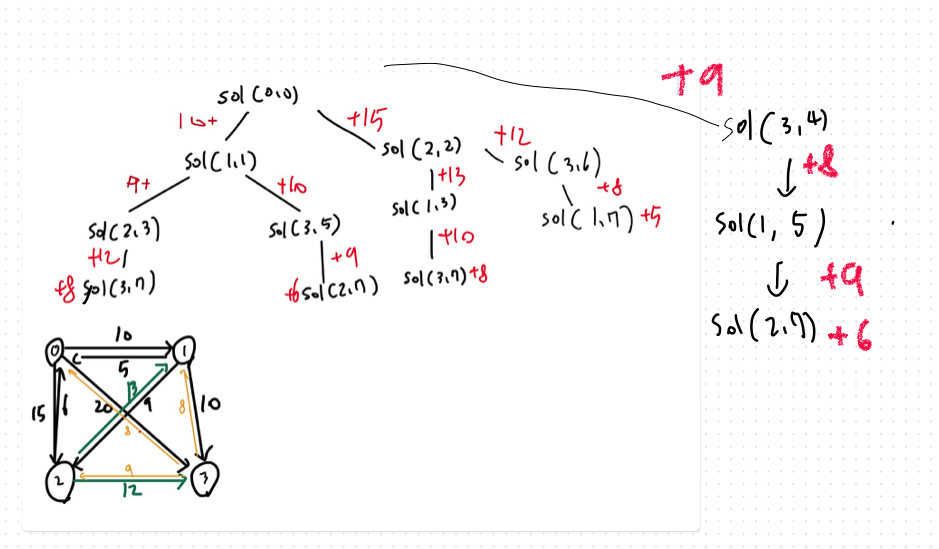
이 코드가 처음에 재귀적으로 돌아서 어째서 dp[2][3] = 20이 나오는지 이해가 안됐다.

여기서 dp[2][3] = 20인 의미는 3이 이진수로 0b11인데 이 의미는 일단 도시 1과 2를 방문했다는 의미이다.
그럼 현재 방문 안한 도시가 3인데 재귀는 바닥조건을 찍고 역으로 거슬러 올라가니까

• 마지막 도시인 3에서 0으로 가는 값 -> 8
• 2에서 3으로 가는 값 -> 12

이 둘을 더하면 20이 되는 것이다. 일단 1에서 2가고 그 다음 경로의 최소값이 20이라는 말이다. 이 정보를 메모이제이션 해놔서 나중에 똑같은 경로를 찾을 일이 생겼을 때 재귀를 또 도는 것이 아니라 dp테이블에서 최소값을 가져와서 사용한다.

dp[1][1]의 의미는 연어가 강을 거슬러 올라오듯이 나머지 도시를 다 방문하고 1로 왔을 때 최솟값이라는 뜻이다. 이 경우에 dp[1][1] = 25이다.

코드

import sys

input = sys.stdin.readline
N = int(input())
W = [list(map(int, input().split())) for _ in range(N)]

dp = [[0] * (1 << N - 1) for _ in range(N)]


def solution(i, route):
    if dp[i][route] != 0:
        return dp[i][route]

    # 현재까지 방문한 도시의 집합(route)이 모든 도시를 방문한 집합(2^(N-1) - 1)과 같은지를 판별하는 조건문
    if route == (1 << (N - 1)) - 1:
        ## 모든 도시를 방문했으면 마지막 도시에서 시작점으로 돌아가는 값
        if W[i][0]:
            return W[i][0]
        else:
            return float("inf")

    min_dist = float("inf")
    for j in range(1, N):
        if not W[i][j]:
            continue
        # 비트마스크(route)를 활용하여 j번째 도시를 방문했으면 1
        # 안했으면 0
        if route & (1 << j - 1):
            continue
        dist = W[i][j] + solution(j, route | (1 << (j - 1)))
        min_dist = min(min_dist, dist)
    dp[i][route] = min_dist

    return min_dist


print(solution(0, 0))
print(dp)

문제 링크