(논문리뷰)An Empirical Evaluation of Generic Convolutional and Recurrent Networks for Sequence Modeling

Abstruct

대부분의 딥러닝 실무자에게 시퀀스 모델링이란 곧 순환 신경망(RNN)을 의미한다. 하지만 최근 연구에서는 합성곱 신경망(CNN)이 오디오 합성, 기계 번역 등의 분야에서 RNN보다 우수한 성능을 보이고 있음을 제시했다. 그렇다면 새로운 시퀀스 모델링 작업이나 데이터셋을 다룰 때 어떤 아키텍처를 선택하는 것이 좋을까? 본 논문에서는 일반적인 합성곱 및 순환 아키텍처를 다양한 표준 작업에서 체계적으로 평가한다. 평가 결과, 간단한 합성곱 신경망 아키텍처가 LSTM 같은 대표적 RNN 구조를 다양한 작업과 데이터셋에서 뛰어넘으며, 보다 긴 효과적 기억력을 보여준다. 따라서 시퀀스 모델링을 무조건 RNN과 연결짓는 일반적 관념은 재고되어야 하며, 합성곱 네트워크가 시퀀스 모델링 작업의 기본 출발점으로 여겨져야 한다는 결론을 내린다.

Introdcution

딥러닝 실무자들은 대체로 시퀀스 모델링 작업에 RNN을 기본 출발점으로 삼는다. 대표적인 딥러닝 교재(Goodfellow 등, 2016)도 RNN을 중심으로 시퀀스 모델링을 설명하고 있으며, 최근의 온라인 강의(Ng, 2018)에서도 RNN을 독점적으로 다루고 있다.

하지만 최근 연구는 오디오 합성(van den Oord 등, 2016), 기계 번역(Gehring 등, 2017) 등 특정 응용 분야에서 합성곱 구조가 RNN을 능가함을 보여주었다. 이는 합성곱 구조의 성공이 특정 분야에만 국한된 것인지, 아니면 전반적으로 시퀀스 처리에서 RNN과의 연관성을 재검토해야 하는지에 대한 질문을 제기한다.

본 연구에서는 폭넓은 시퀀스 모델링 작업에서 합성곱 및 순환 아키텍처의 성능을 체계적으로 비교한다. 특히 RNN 모델의 성능 평가에 자주 사용되는 다양한 작업들(음악 생성, 문자·단어 수준 언어 모델링, 합성 스트레스 테스트)을 사용했다.

이를 위해 최근 연구를 반영한 간단한 구조의 범용 시계열 합성곱 네트워크(Temporal Convolutional Network, TCN)를 제안하고, 이를 표준 LSTM, GRU 같은 RNN 구조와 비교했다.

결과는 TCN이 다양한 시퀀스 모델링 작업에서 대표적 RNN을 압도적으로 뛰어넘음을 보여준다. 특히 TCN은 이론적으로 무한한 과거 정보를 다룰 수 있다는 RNN의 장점에도 불구하고, 실제로는 더 긴 효과적 기억력을 가지고 있음이 밝혀졌다.

본 논문은 지금까지 발표된 합성곱과 순환 네트워크의 시퀀스 모델링 비교 연구 중 가장 포괄적이며, 시퀀스 모델링을 무조건 RNN과 결합시키던 기존 관념을 바꿀 필요성을 강조한다. 따라서 더 단순하고 명확하며 성능이 우수한 TCN 구조가 시퀀스 작업의 새로운 기준점이 될 수 있다.

Background

합성곱 네트워크는 오랜 시간동안 시퀀스 모델링에 사용되어 왔으며, 최근 오디오 합성 및 기계 번역에서 두드러진 성과를 냈다. 반면 RNN은 언어 모델링, 기계 번역 등의 분야에서 큰 인기를 끌었다. 특히 LSTM이나 GRU가 복잡한 시간 의존성을 처리하는 데 효과적이어서 널리 활용되었다.

지금까지 RNN 구조 비교를 위한 많은 경험적 연구가 진행되었으나, 합성곱과 RNN 구조 간의 광범위한 비교는 이루어지지 않았다. 본 논문에서는 일반적인 합성곱 구조와 RNN을 대표적 시퀀스 작업에서 체계적으로 비교한다.

Temporal Convolutional Networks (TCN)

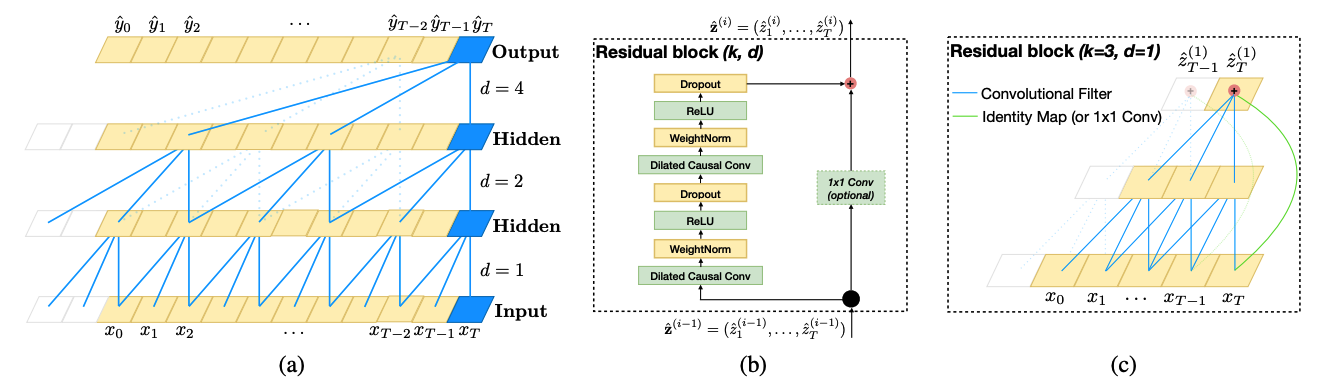
TCN은 시퀀스 길이가 동일한 출력을 생성하는 1D 합성곱 네트워크로, 미래 정보가 과거로 새어 들어가지 않는 인과적(causal) 합성곱을 사용한다. 긴 시계열 과거 정보를 다루기 위해 딥 네트워크와 dilation(확장) 합성곱을 사용한다. 또한 안정적인 학습을 위해 잔차 연결(residual connections)을 도입했다.

TCN의 장점은 병렬성(parallelism), 유연한 receptive field 조정, 안정적 기울기(gradient) 전파, 낮은 학습 메모리 요구량, 다양한 입력 길이 처리 능력 등이다. 단점으로는 평가 시 원본 데이터를 유지해야 하고, 영역 간 전이(transfer) 시 파라미터를 변경해야 할 수 있다는 점이 있다.

Causal Convolutions

앞서 설명했듯 TCN은 입력과 같은 길이의 출력을 생성하며, 미래의 정보가 과거로 흘러가지 않도록 보장해야 한다. 이를 위해 TCN은 1D Fully-Convolutional Network(FCN)을 사용하며, 각 은닉층(hidden layer)은 입력층과 길이가 같으며, padding을 추가하여 층의 길이를 유지한다. 또한 TCN은 "인과적 합성곱(causal convolution)"을 사용하여 특정 시간 t의 출력이 오직 현재 및 과거 시간의 입력과만 합성곱되도록 제한한다.
TCN은 다음과 같이 표현된다:

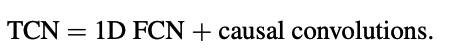
기본적인 인과적 합성곱의 단점은 long memory을 얻기 위해 매우 깊은 네트워크 또는 큰 필터(filter)가 필요하다는 것이다. 이런 문제를 해결하기 위해 dilation 합성곱을 사용하여 긴 유효 과거 정보를 효과적으로 확보한다.

Dilated Convolutions

일반적인 합성곱은 과거 정보를 층의 깊이만큼 선형적으로만 바라볼 수 있다. 이는 긴 시퀀스를 다루기 어렵게 만든다. 확장 합성곱(dilated convolution)은 합성곱 필터 간격에 빈 공간을 두어, 층의 깊이가 깊어질수록 더 많은 과거 정보에 지수적으로 접근할 수 있게 만든다.
확장 합성곱 연산은 아래와 같이 표현된다:

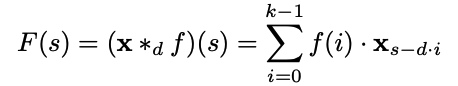
여기서 𝑑는 확장 계수(dilation factor), 𝑘는 필터 크기이며, 이때 더 큰 확장 계수를 사용하면 합성곱이 더 멀리 있는 입력 정보를 볼 수 있다.

Sequence Modeling Tasks

합성곱 및 순환 신경망은 다양한 시퀀스 모델링 작업(Adding 문제, 순차적 MNIST, 복사 메모리 문제, 음악 모델링, 언어 모델링)에서 평가되었다. 동일한 파라미터 수로 두 구조를 공정히 비교한 결과, 일반적인 TCN이 모든 작업에서 대표적 RNN(LSTM, GRU 등)을 명백히 능가했다.
특히 긴 시계열 정보를 유지하는 능력에 있어 TCN이 월등히 우수하다는 점이 확인되었다.

Conclusion

이 논문은 다양한 시퀀스 작업에서 일반적 합성곱 아키텍처가 순환 아키텍처보다 우수함을 경험적으로 입증했다. 결과적으로 시퀀스 모델링과 RNN의 밀접한 관계는 과거의 유산이며, 현재는 dilation 및 잔차 연결 같은 기술을 갖춘 TCN이 더욱 효율적인 선택일 수 있다. 향후 합성곱 네트워크가 시퀀스 모델링의 새로운 표준으로 자리잡을 가능성을 제안한다.