오늘은 머신러닝에서 모델을 학습시키는 가장 중요한 요소인 경사하강법(Gradient Descent)에 대해 글을 작성하려한다.
경사하강법이 무엇인가?
먼저 경사하강법이 무엇인지에 대해 정리한다.
위키백과에서 정의하는 경사하강법은 "1차 근삿값 발견용 최적화 알고리즘으로, 함수의 기울기(경사)를 구하고 경사의 반대 방향으로 계속 이동시켜 극값에 이를 때까지 반복시키는 것"이라고 나온다.
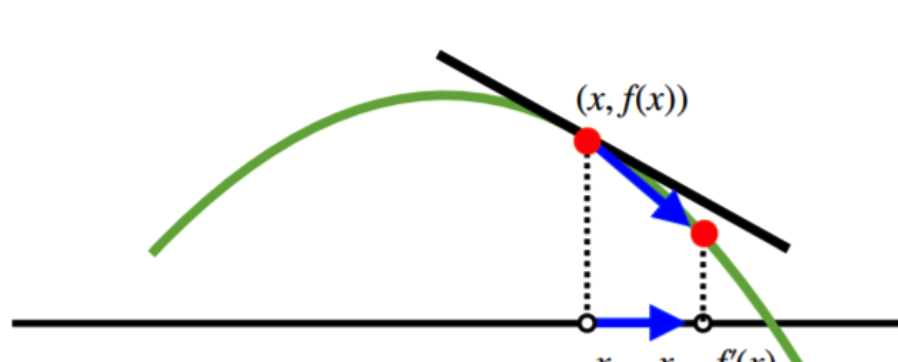
조금 풀어서 생각하면 경사하강법은 아래의 그림과 같이 함수의 기울기값을 구한 다음 그 값의 반대 방향으로 기울기값에 변화를 주어 함수의 최소값을 찾을 때까지 반복하는 방법이다.
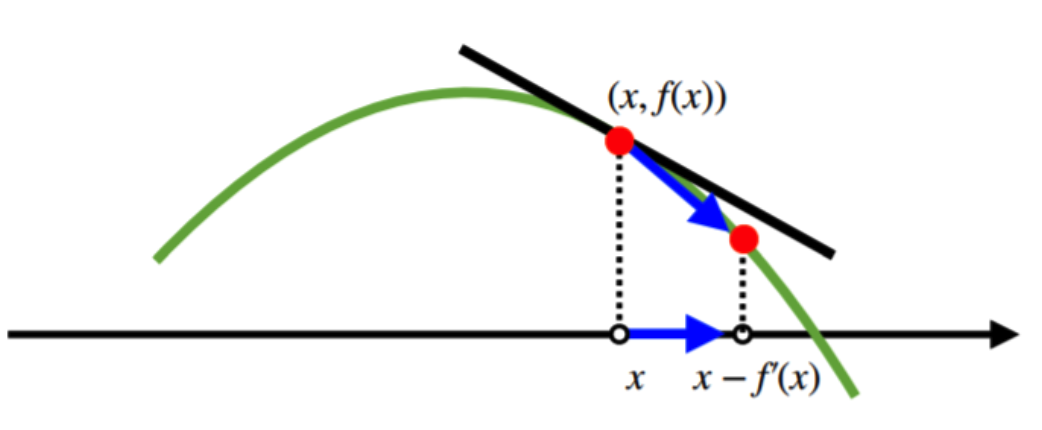
그에 반대되는 개념으로는 경사상승법이 있으며 이것은 경사하강법과 유사하지만 함수의 최대값을 찾을 때까지 반복한다는 점이 다르다.
수식으로 풀이를 하자면 아래와 같이 설명할 수 있다.
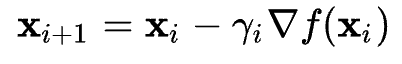
최적화할 함수 f(X)라고 하였을 때, 초기 시작점 를 지정하고 현재 가 주어졌을 때, 경사하강법을 통해 업데이트할 값을 라고 표현한다. 이때 감마는 학습률(learning rate)가 되며 이때 값에 따라 지역 최적해 문제가 발생할수도 있으며 해소 될 수 있다.
그러므로 구한 값이 전역적인 최적해라는 것을 보장할 수 없으므로 지역 최적해에 빠지지 않기 위해 다양한 시작점에 대해 경사하강법을 적용하거나 감마, 즉 학습률을 크게하거나 적게 조절한다.
프로그램 코드 예제(출처 위키백과)
x_old = 0
x_new = 6 # The algorithm starts at x=6
eps = 0.01 # step size
precision = 0.00001
def f_prime(x):
return 4 * x**3 - 9 * x**2
while abs(x_new - x_old) > precision:
x_old = x_new
x_new = x_old - eps * f_prime(x_old)
print(f"Local minimum occurs at: {x_new}")경사하강법의 문제점
경사하강법의 문제점으로는 크게 두가지 있다.
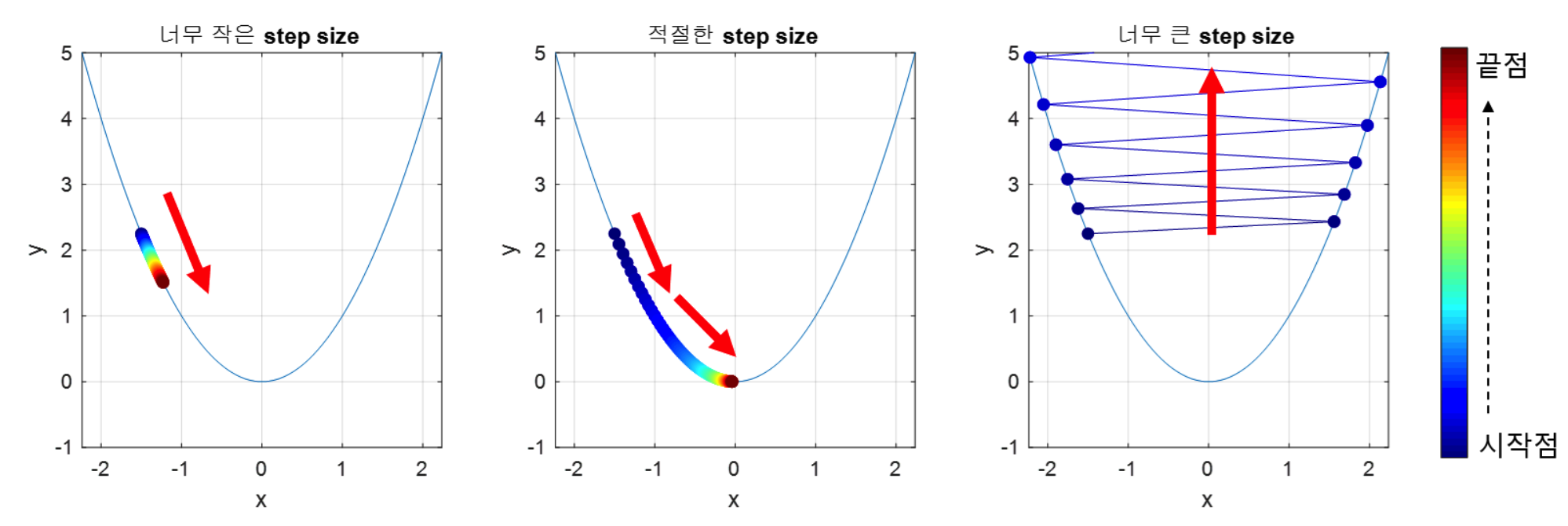
1) 첫번째로는 적절한 step size를 조절이 필요하다. 앞서 설명한 내용과 같이 학습률을 자세히 설명하자.
step size가 큰 경우 함수의 기울기의 이동거리가 커지므로 빠른 속도로 최저점에 수렴할 수 있다. 학습을 진행하다보면 시간적 요인은 매우 중요하다. 모델을 비교하거나 성능 향상을 위해 실험을 하는 중이라는 가정을 하였을 때 하나의 모델에 많은 시간이 소요된다면 실험에 차질이 생길 수 있도 있다. 그러므로 빠른 속도로 최저점에 도달하여 학습 종료가 되는 경우는 이상적인 경우이다. 하지만 step size를 크게 설정해버리면 함수의 최저점에 수렴하지 못하고 함수의 값이 계속 커지는 방향으로 진행될 수도 있기 때문에 유의해야 한다. 이를 해결하기 위해 여러가지 학습 스케줄러를 활용하거나 학습률 조절을 위한 기법들이 활용된다.
반대로 step size가 너무 작은 경우는 큰 경우처럼 값이 발산하여 최저점에 도달하지 못하는 경우는 안생기지만 최저점을 찾아가는 데 많은 시간이 소요된다.
우리는 한정된 시간을 살아가기 때문에 선택과 집중이 필요하다.
2) 두번째로는 Local minima 문제이다. 앞서 설명한 내용과 같이 지역 최적해(Local minima)에 빠져 계속 헤어나오지 못하고 결국 지역최적해를 전역최적해라고 가정하고 학습을 종료하게 되는 문제이다. 이러한 문제점을 해결하기 위해 많은 시도 등이 있다. 근본적으로 완벽하게 지역최적해를 벗어났다고 정의하기는 힘들지만 단계적인 연구를 통해 다양한 방법론이 나왔다.
대표적으로 Momentum, Nesterov Accelerated Gradient(NAG), Adagrad, Adadelta,RMSprop,Adam 등이 있다. 자세한 내용은 추후 포스팅 하는 것으로 하고 간단하게 정리하고자 한다.
- Momentum이란 관성을 의미하며, 이전 gradient의 방향성을 담고있는 momentum 인자를 통해 흐르던 방향을 어느 정도 유지시켜 Local minima에 빠지지 않게 만든다. 즉 관성을 이용하여, 학습속도를 더 빠르게 하고, 변곡점을 잘 넘어갈 수 있도록 해주는 역할을 수행한다.
- NAG는 모멘텀과 비슷한 역할을 수행하는 Look-ahead gradient 인자를 포함하여, 알파라는 accumulate gradient가 gradient를 감소시키는 역할을 한다. 모멘텀과 다른 점은 미리 한 스템을 옮겨가본 후에 어느 방향으로 갈지 정한다.
- Adagrad란 뉴럴넷의 파라미터가 많이 바뀌었는지 적게 바뀌었는지 확인하고, 적게 변한건 더 크게 변하게 하고, 크게 변한건 더 작게 변화시키는 방법이다. Adagrad는 sum of gradient squares를 사용하는데, 이는 그래디언트가 얼마만큼 변했는지 제곱해서 더하는 것이므로 계속 커진다는 문제가 발생한다. 그래디언트의 제곱합이 계속 커지게 되면 분모가 무한대에 가가워지게 되며, 가중치 업데이트가 되지 않게 되어, 뒤로 갈수록 학습이 점점 안되는 문제점이 발생한다.
- Adadelta는 Exponential Moving Average(EMA)를 사용하여, Adagrad의 그래디언트의 제곱합이 계속 커져 학습이 진행이 어려워지는 문제를 막을 수 있다. EMA는 현재 타임스텝으로부터 윈도우 사이즈만큼의 파라미터 변화를 반영하는 역할을 하는데, 이전의 값을 모두 저장하는 것이 아닌, 이전 변화량에 특정 비율을 곱해 더한 인자를 따로 두는 방식이다. 그래서 Adadelta에는 학습률이 없다.
추후 경사하강법의 알고리즘들에 대해 자세히 정리하는 포스팅을 만들 예정이다.