1. Cost Function (손실 함수)란?
개념 및 정의
Cost Function(손실 함수)은 모델이 예측한 값과 실제 값 사이의 차이를 정량적으로 측정하는 함수입니다. 모델이 학습하는 동안 목표는 손실 함수를 최소화하는 방향으로 가중치와 편향을 조정하는 것입니다.
쉽게 말해, 손실 함수는 모델이 얼마나 "잘못 예측했는지"를 평가하는 기준입니다. 손실 함수의 값이 작을수록 모델이 더 정확하게 예측하고 있다는 의미이며, 반대로 값이 클수록 모델의 예측이 실제 값과 많이 차이가 난다는 것을 의미합니다.
대표적인 Cost Function 종류
1) 회귀(Regression)에서 사용하는 Cost Function
회귀 문제에서는 연속적인 수치를 예측하기 때문에, 예측값과 실제값의 차이를 기반으로 손실을 계산합니다.
MSE (Mean Squared Error, 평균 제곱 오차)
예측값과 실제값의 차이를 제곱한 후 평균을 내는 방식입니다.
차이를 제곱하기 때문에 큰 오차일수록 손실이 더 커지는 특징이 있습니다.
이상치(Outlier)에 민감하지만, 일반적으로 많이 사용됩니다.
MAE (Mean Absolute Error, 평균 절대 오차)
오차의 절대값을 취하여 평균을 계산하는 방식입니다.
이상치에 덜 민감하지만, 미분이 불가능한 점이 있어 최적화가 어려울 수 있습니다.
2) 분류(Classification)에서 사용하는 Cost Function
분류 문제에서는 클래스 확률을 예측하고, 이를 실제 레이블과 비교하여 손실을 계산합니다.
Binary Cross-Entropy (이진 분류 손실 함수)
이진 분류에서 사용되며, 예측값이 실제 레이블과 얼마나 가까운지를 평가합니다.
예측 확률이 실제 값에 가까울수록 손실이 작아지고, 반대로 멀어질수록 손실이 커집니다.
Categorical Cross-Entropy (다중 분류 손실 함수)
다중 클래스 분류에서 사용되며, Softmax 활성 함수와 함께 적용됩니다.
클래스 확률 분포를 비교하여 손실을 측정합니다.
2. Activation Function (활성 함수)란?
개념 및 정의
Activation Function(활성 함수)은 뉴런의 입력 값을 변환하여 출력하는 함수입니다. 이 함수는 딥러닝 모델이 비선형성을 학습할 수 있도록 도와주는 역할을 합니다.
만약 활성 함수를 사용하지 않는다면, 뉴런의 출력이 단순한 선형 함수로 표현되어 신경망의 깊이를 늘려도 복잡한 패턴을 학습할 수 없습니다.
대표적인 Activation Function 종류
1) 선형 활성 함수 (Linear Activation)
입력값을 그대로 출력하는 함수.
비선형성을 제공하지 않기 때문에 딥러닝 모델에서 잘 사용되지 않음.
2) 비선형 활성 함수 (Non-Linear Activation)
비선형성을 도입하면 모델이 복잡한 데이터 패턴을 학습할 수 있습니다.
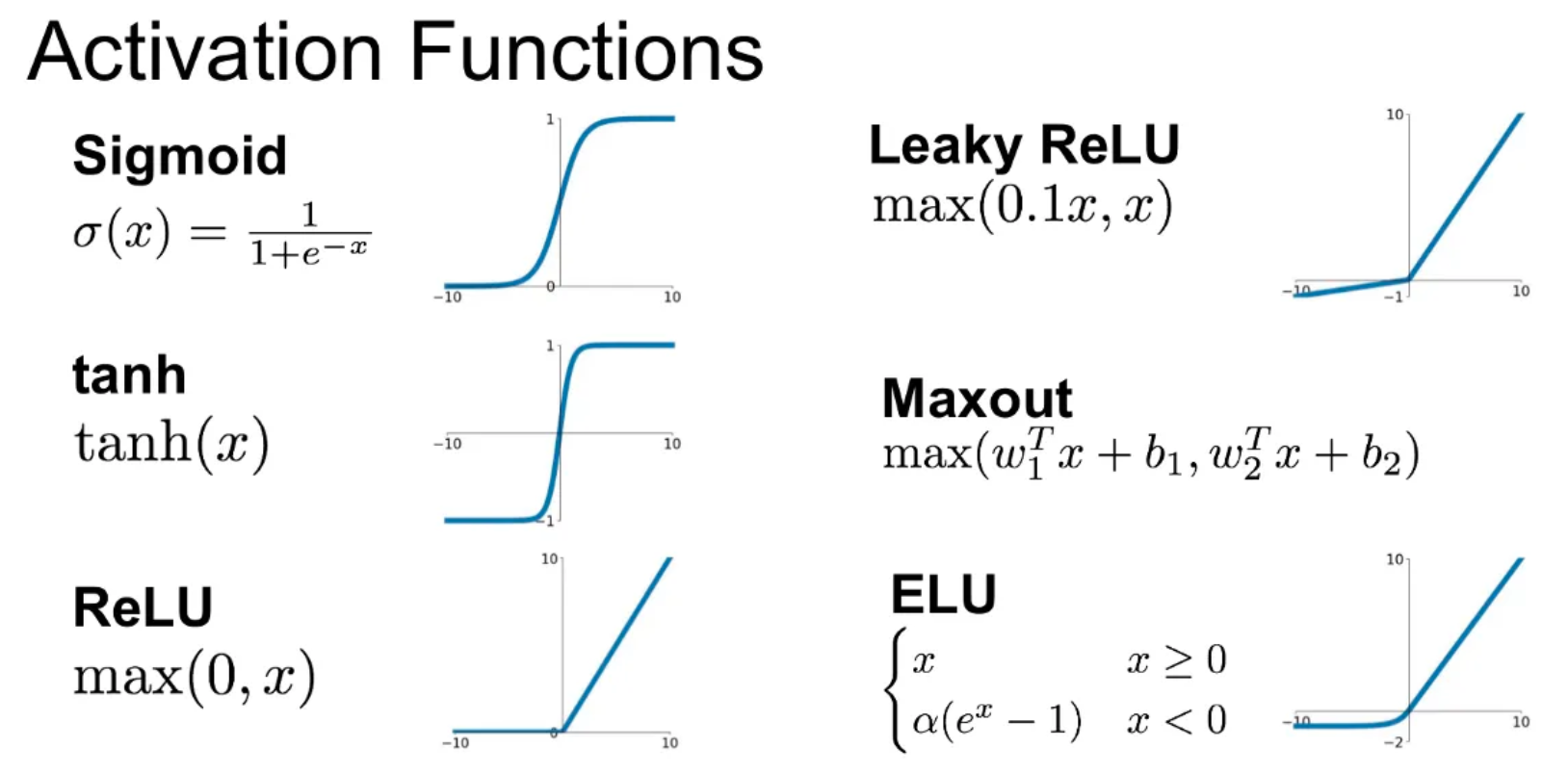
ReLU (Rectified Linear Unit)
양수 값은 그대로 출력, 음수 값은 0으로 변환.
기울기 소실 문제(Vanishing Gradient)를 해결하고, 연산량이 적어 학습 속도가 빠름.
하지만, 일부 뉴런이 계속 0이 되는 문제(Dead Neuron Problem)가 발생할 수 있음.
Leaky ReLU
ReLU의 문제점(Dead Neuron Problem)을 보완하기 위해 음수 영역에서 작은 값(α)을 허용.
Sigmoid
출력을 0과 1 사이의 값으로 변환하여 확률처럼 사용할 수 있음.
하지만, 기울기 소실 문제(Vanishing Gradient)로 인해 깊은 네트워크에서는 잘 사용되지 않음.
Tanh (Hyperbolic Tangent)
출력이 -1에서 1 사이에 분포하여, 평균이 0에 가까워지므로 학습이 더 안정적.
하지만, Sigmoid와 마찬가지로 기울기 소실 문제가 발생할 수 있음.
Softmax
다중 클래스 분류에서 확률 값을 얻는 데 사용됨.
모든 출력의 합이 1이 되도록 변환.
3. Cost Function과 Activation Function의 조합
회귀 문제: Linear 또는 ReLU 활성 함수 + MSE 또는 MAE 손실 함수
이진 분류: Sigmoid 활성 함수 + Binary Cross-Entropy
다중 분류: Softmax 활성 함수 + Categorical Cross-Entropy