평가 지표(2)

서론

이번 포스팅은 글또 10기 두번째 작성글이다.
2주라는 기간이 꽤 여유있는 기간이라고 생각이 들었지만 매번 제출일에 작성과 수정을 반복하고 있다.
평가지표는 첫번째 포스팅에 작성하였던 내용으로 업무를 하며 추가로 활용한 지표들에 대해 정리하는 것을 목적으로 한다.
1. RRMSE
2. WMAPE
두가지 지표가 업무에서 활용 및 제시되었던 지표이고 그 이외의 지표들도 찾아보았다.
3. RSE
4. RMSLE
5. NRMSE

---

회귀모델 평가지표 (2)

1. RRMSE

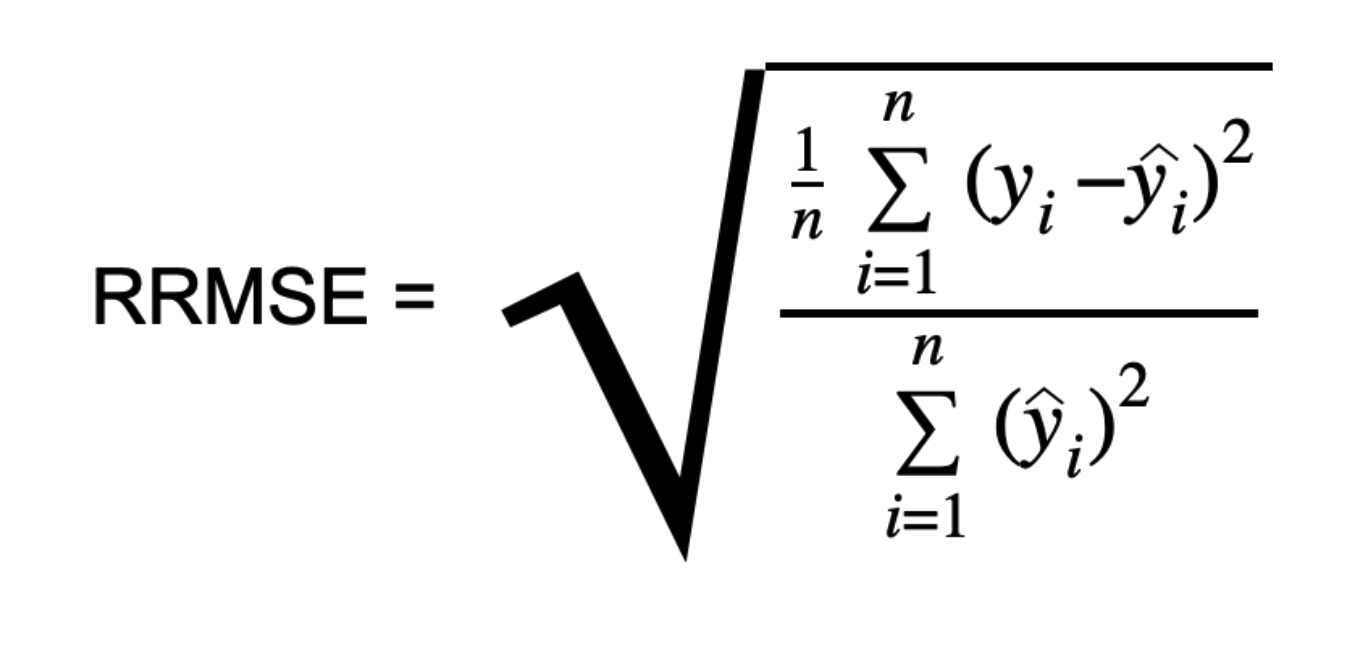
Relative Root Mean Squared Error(RRMSE)는 머신러닝에서 자주 사용되는 RMSE의 변형으로, 대상 변수 범위에 대한 예측 정확도를 측정합니다. RMSE를 대상 변수 범위로 정규화하고 직관적인 비교를 위해 백분율로 표시합니다. RRMSE는 잔차를 실제 값에 대해 스케일하여 다양한 측정 기술을 비교할 수 있도록 합니다.

일반적인 비교 기준

• RRMSE < 10% : Excellent
• 10% < RRMSE < 20% : Good
• 20% < RRMSE < 30% : Fair(보통)
• 30% < RRMSE : poor

Code(python)

def relative_root_mean_squared_error(true, pred):
	num = np.sum(np.square(true - pred))
    den = np.sum(np.square(pred))
    squared_error = num/den
    rrmse_loss = np.sqrt(squared_error)
    return rrmse_loss

2.WMAPE

Weighted Mean Absolute Error(WMAPE) 머신러닝에서 자주 사용되는 직관적인 MAPE 한계를 극복하기 위해 고안된 지표로, 이때 WMAPE는 분모의 실제 값의 합을 분모로 하여 기존 MAPE에서 발생하는 실제 값이 0일 경우 오차가 무한히 커지는 문제를 해결하였습니다.

Code(python)

def Weighted_mean_absolute_error(true,pred):
    wmape = np.sum(np.abs(actual-forecast))/np.sum(actual)
    return wmape
	

3.RSE

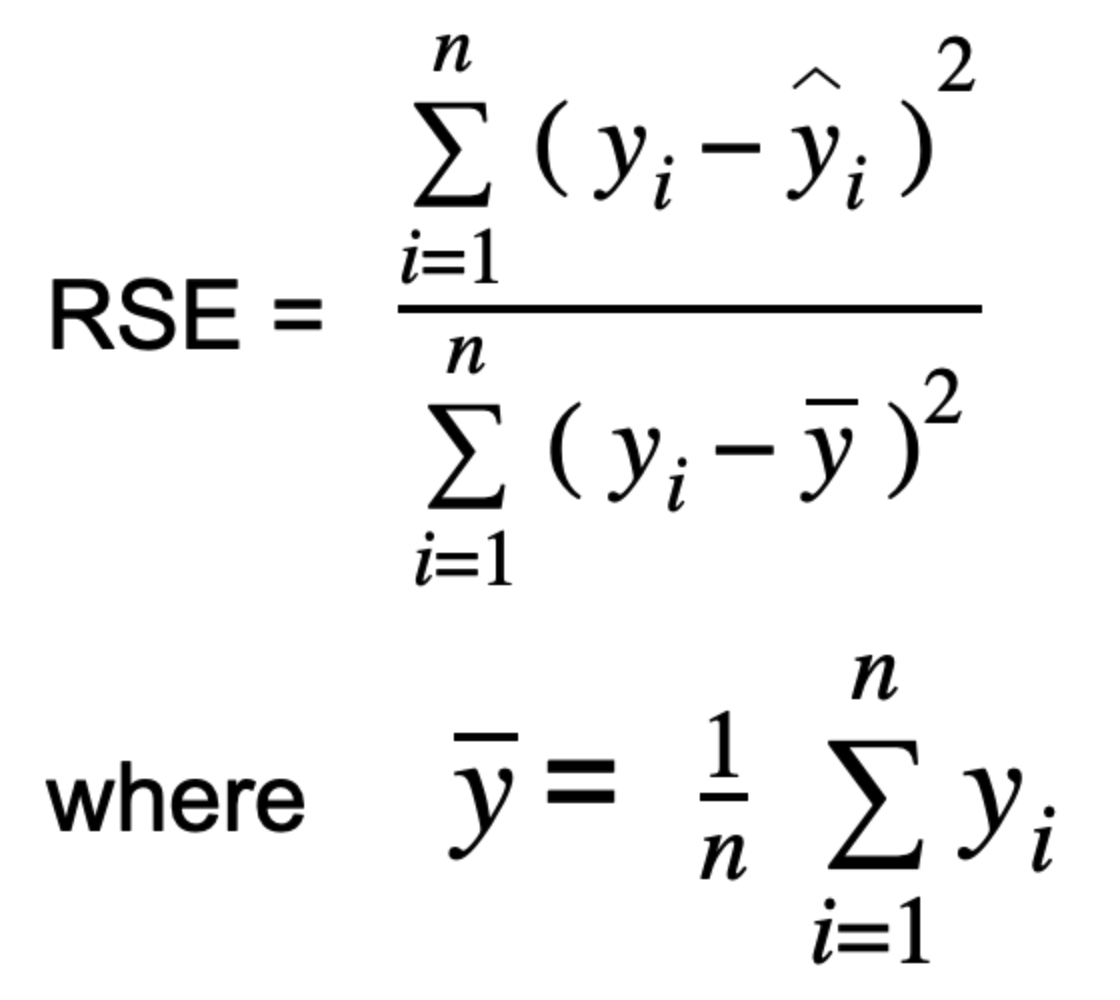
Relative Squared Error(RSE)는 상대제곱오차로 평균제곱오차(MSE)를 실제 데이터와 평균의 차이를 제곱으로 나눕니다. 즉 모델의 MSE를 예측 값으로 평균을 사용하는 모델의 MSE로 나눕니다.
예측 값과 실제 값 사이 차이를 제곱한 것을 기준으로 산정한 0과 1 사이의 상대적 평가지표이다. 이 값은 0에 가까울수록 모델의 정확도가 높다는 것을 의미하며, 서로 다른 스케일을 가지고 있는 모형을 비교할 때 용이하다.

Code(python)

def relative_squared_error(true, pred):
    true_mean = np.mean(true)
    squared_error_num = np.sum(np.square(true - pred))
    squared_error_den = np.sum(np.square(true - true_mean))
    rse_loss = squared_error_num / squared_error_den
    return rse_loss

4.RMSLE

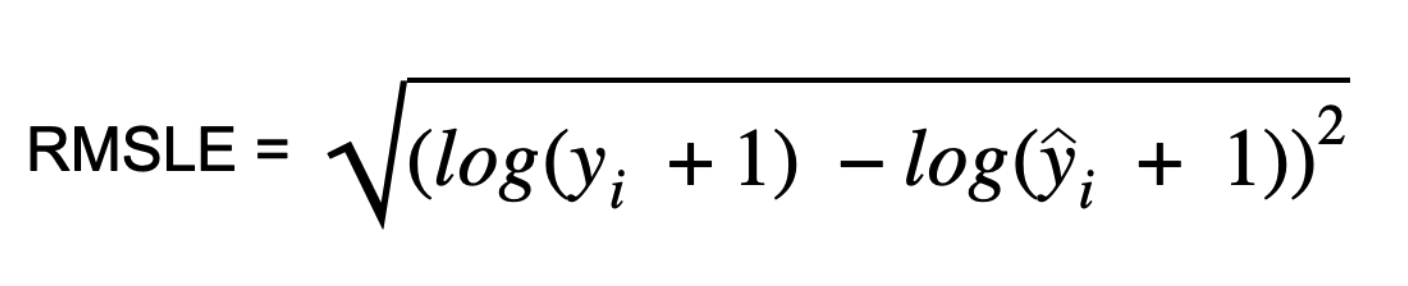
Root Mean Squared Log Error(RMSLE)는 실제 값과 예측 값에 로그를 적용한 다음 차이를 구하여 계산한다.
RMSLE는 두 값의 비율에 더 집중하며, 이는 큰 값의 오차가 작은 값의 오차보다 더 크게 평가되지 않도록 합니다. 로그로 인하여 예측 값이 실제 값보다 작으면 모델에 더 많은 패널티를 주고 예측 값이 실제 값보다 크면 모델에 비교적 적은 패널티를 줍니다. 따라서 모델은 과대평가보다 과소평가에 대해 더 큰 패널티를 받는다.
그러므로 과대 평가에 대해 신경쓰지 않지만 과소평가는 허용되지 않는 상황에서 도움이 될 수 있다.

Code(python)

def root_mean_squared_log_error(true, pred):
    square_error = np.square((np.log(true + 1) - np.log(pred + 1)))
    mean_square_log_error = np.mean(square_error)
    rmsle_loss = np.sqrt(mean_square_log_error)
    return rmsle_loss

5.NRMSE

Normalizaed Root Mean Squared Error(NRMSE)는 일반적으로 스칼라 값을 나누어 계산합니다.
다음과 같은 다양한 방법이 있다.

• RMSE / maximum value in the series(최대값)
• RMSE / mean(평균)
• RMSE / difference between the maximum and the minimum values (if mean is zero)(평균이 0인경우 최대값과 최소값의 차이)
• RMSE / standard deviation(표준편차)
• RMSE / interquartile range(사분위 범위)

Code(python)

# implementation of NRMSE with standard deviation
def normalized_root_mean_squared_error(true, pred):
    squared_error = np.square((true - pred))
    sum_squared_error = np.sum(squared_error)
    rmse = np.sqrt(sum_squared_error / true.size)
    nrmse_loss = rmse/np.std(pred)
    return nrmse_loss

---

참고
https://www.analyticsvidhya.com/blog/2021/10/evaluation-metric-for-regression-models/#h-relative-root-mean-squared-error-rrmse