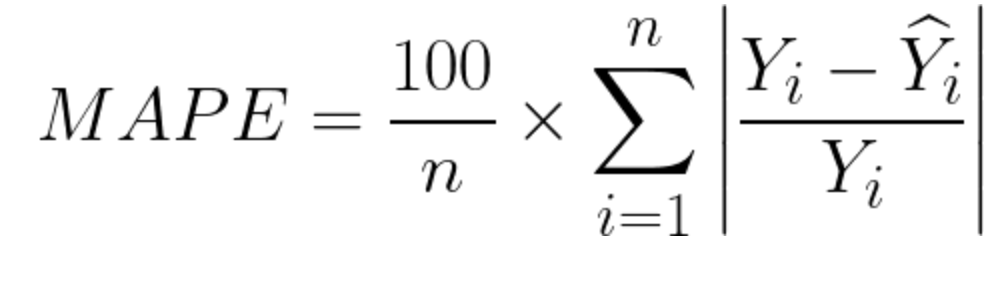서론

이번에는 글또 10기에 참여하고 처음 작성하는 글이다.
블로그를 꾸준하게 작성하는 것을 목표로 글또를 신청하였지만 역시나 일과 휴식 등 여러가지 핑계를 대고 있는 중이다. 그래도 기간 안에 글을 작성해야한다는 압박감을 느끼며 첫번째 글을 적어본다.
글의 주제는 데이터 사이언스 관련 내용으로 작성하는 것을 우선적으로 생각해보았다.
그 중에서 최근 경험상 평가지표가 중요하다는 것을 체감하고 있는중으로 종류별로 정리하는 글을 작성해보려고 한다. 수식에 대한 이해와 파이썬 코드를 함께 작성하여 추후 필요할 때 활용하는 것을 목표로 하려고한다.
또한 지속적으로 업데이트 하는 것을 목표로 하고 있다.

---

회귀 모델의 평가지표

1.MAE

• 모델의 예측값과 실제값의 차이를 절대값의 평균으로 나타낸 수치
• 절대값을 취하기 때문에 가장 직관적으로 알 수 있는 지표이다.(해석이 용이)
• 절대값을 취하기 때문에 모델이 실제보다 낮은 값으로 예측하는지 높은값으로 예측하는지 알 수 없다.

특징

1.손실함수가 오차와 비례하여 일정하게 증가하는 특징이 있음
2.Outlier에 강건하다
-> outliear가 있어도 최대한 잘 추정된 데이터들의 특성을 반영할 수 있기 때문에 통계적으로 중앙값과 연관이 깊다.

2.MSE

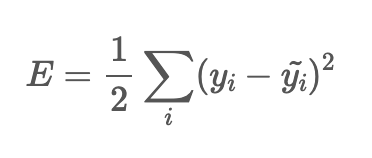
• 모델의 예측값과 실제값의 차이를 제곱한 수치로 면적의 합이다.
• 제곱을 하기 때문에 특이치에 만감하다.

  특징

  1. 오차가 커질수록 손실 함수값이 빠르게 증가하는 특징이 있음
  2. 통계학에서 많이 사용되며 회귀모델에서 이용된다.
  3. 단점으로 제곱으로 인해 숫자의 규모가 실제 데이터의 스케일에 비해 비대해질수 있음

3.RMSE

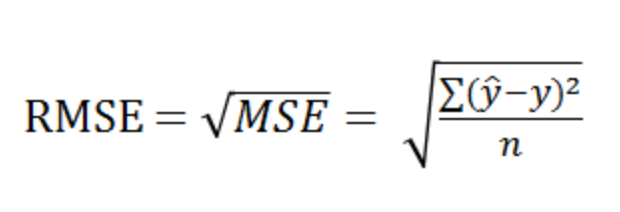
• MSE에 루트를 씌워 사용한다
• RMSE를 사용하면 오류 지표를 실제값과 유사한 단위로 다시 변환하여 해석을 쉽게한다.
• 예측 대상의 크기에 영향을 바로 받는다.
• MAE보다 특이치에 강하다

4.MAPE

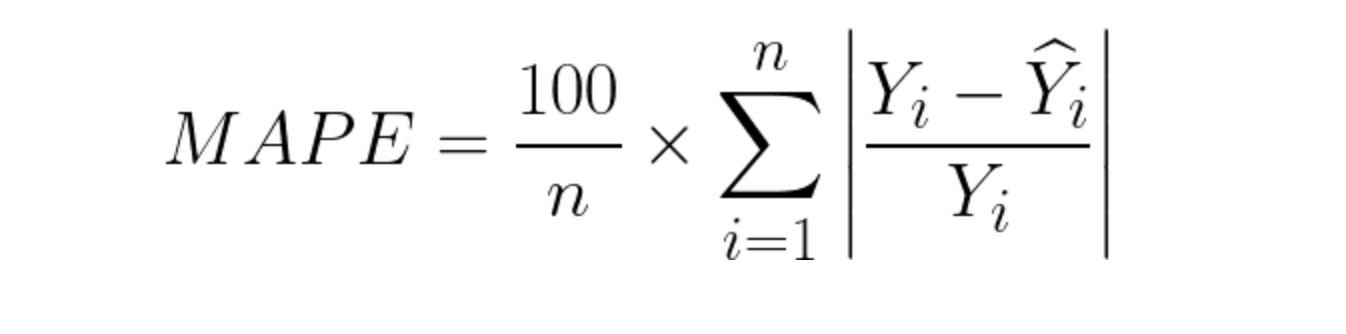
• MAPE는 Mean Absolute Percentage Error의 약자로 회귀모델이 잘 학습되었는지 확인할 때 많이 활용되는 평가지표이다.
• MAPE 장점
  • 0~100% 사이의 확률 값을 가지기 때문에 결과 해석에 용이하다.
  • 데이터 값의 크기보다 비율에 관련된 값을 가지므로 다양한 모델과 데이터의 성능을 비교할 때 용이하다.
• MAPE 단점
  • 실제 정답 값에 0이 존재하는 경우 MAPE 계산이 불가능함
  • 이러한 경우 대체하는 평가지표를 사용해야함 (SMAPE, WMAPE 등이 있으며 분모가 0일 경우 비교적 계산의 여유가 생긴다.)
  • 실제 정답 값이 0에 가까운 매우 작은 값인 경우 MAPE값이 매우 커질 수 있다.

5.SMAPE

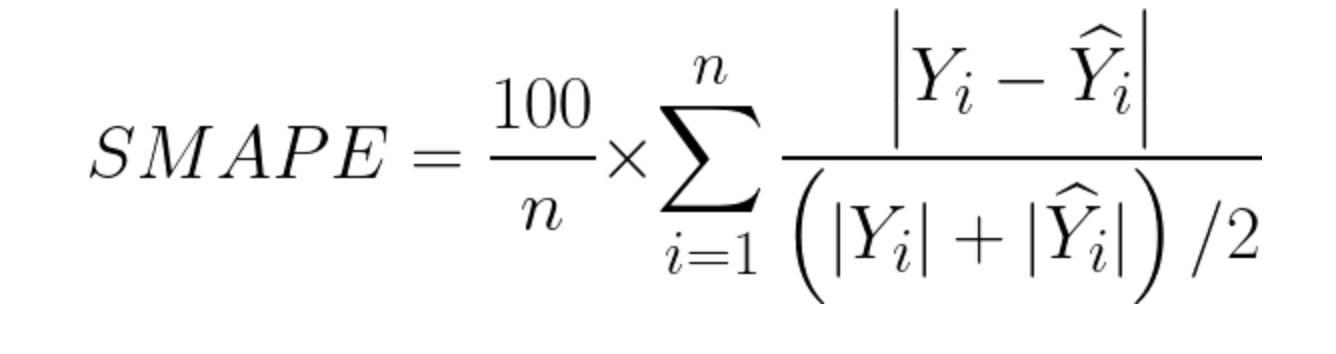
• SMAPE는 Symmetirc Mean Absolute Percentage Error의 약자로 회귀모델이 잘 학습되었는지 확인할 때 많이 활용되는 평가지표입니다.
• MAPE가 가진 한계점을 보완하기 위하여 고안된 평가지표이며 가장 큰 차이점은 MAPE는 오차를 실제값으로 나누는 반면 SMAPE는 실제 값과 예측값의 평균으로 나눈다.
• SMAPE 장점
  • 0~200% 사이의 확률 값을 가지기 때문에 결과 해석이 용이하다.
  • MAPE와 다르게 실제 정답값에 0이 존재해도 계산이 가능하다. 그렇지만 예측값도 0이라면 같은 문제가 발생할 수 있다.
• SMAPE 단점
  • 예측 값이 실제 정답 값보다 작을 때 분모가 더 작아지기 때문에 계산되는 오차가 커지는 현상이 발생한다.
  • 실제 정답 값 또는 예측 값이 0인 경우 자동적으로 SMAPE값의 크기가 최대로 도출된다.