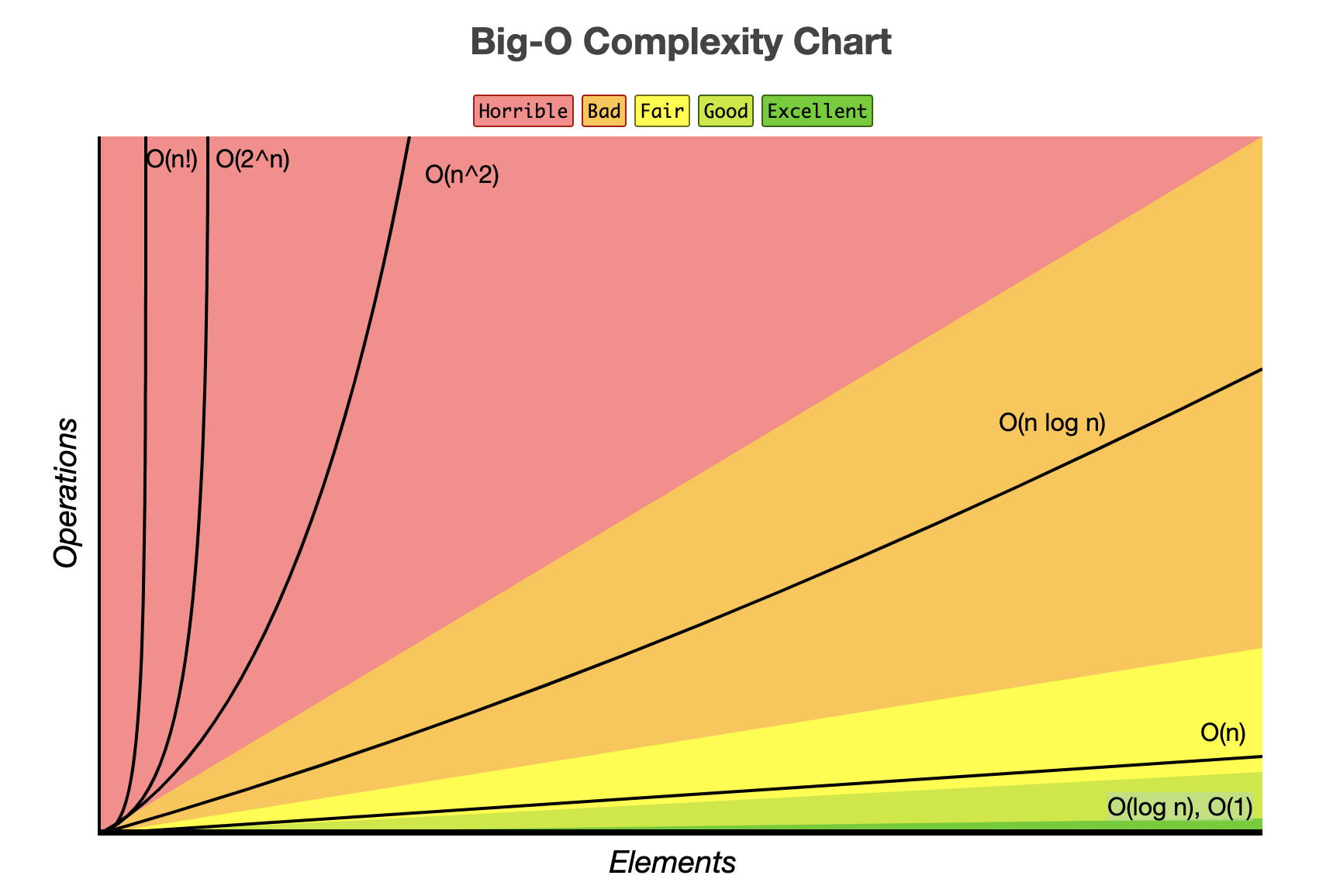
시간복잡도
Big-O(빅-오) , Big-Ω(빅-오메가) ,Big-θ(빅-세타)
최악 , 평균 , 최선 인경우 표기법이다. 알고리즘은 최악의 경우를 대비하여 나타내는 방법을 사용한다.
크게 네가지 시간 복잡도가 있다. O(1) , O(log N) , O(N) , O(N²)
O(1)
constant complexity 라고한다. 입력값의 크기와 상관없이 출력값을 얻을수 있다.
배열의 경우를 코드로 확인하면 길이가 몇인지는 상관없다.
fuction O_one(arr,idx){
return arr[idx];
}
const arr = [1,2,3,…10000]
const idx = 2;
O_one(arr,idx); // 3O(n)
linear complexity 라고하며 입력값이 증가할수록 시간도 증가하는 비례관계이다.
그래프로 봤을때 X축과,Y축이 가 함께 증가한다. (입력값이 1 증가시 , 실행시간도 1초씩 증가)
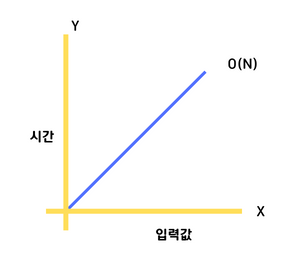
만약 입력값이 1 증가시 실행 시간이 2,4,5배 증가하면 O(2N), O(4N), O(5N) 으로 볼 수있으나, 입력값이 커지면 커질수록 계수(n 앞에 있는 수)의 의미(영향력)가 점점 퇴색되기 때문에 O(N) 으로 표기한다.
function O_N(num){
let result = '';
for(let i =0; i < num; i++ ){
result += i
}
return result
}
let num = 10000;
O_N(num); // '0123456 …9999'O(log n)
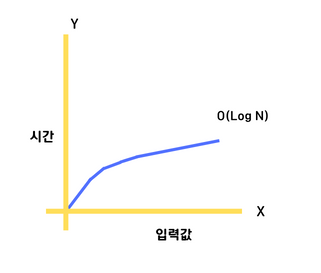
logarithmic complexity 라고하며, Big-O표기법중 O(1) 다음으로 빠른 시간 복잡도를 가진다.
O(n²)
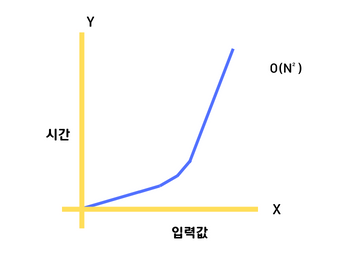
quadratic complexity라고 부르며, 입력값이 증가함에 따라 시간이 n의 제곱수의 비율로 증가한다.
입력값이 5인 경우 실행시간이 제곱인 25초가 걸린다면 간 복잡도는 O(n²)라고 표현한다.
n이 커질수록 지수가 주는 영향력이 점점 퇴색되어 n³과 n⁵ 도 모두 O(n²)로 표기한다.
O(2ⁿ)
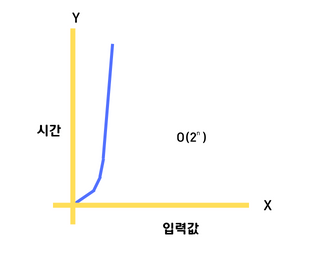
exponential complexity라고 부르며 Big-O 표기법 중 가장 느린 시간 복잡도를 가진다.
구현한 알고리즘의 시간 복잡도가 O(2ⁿ)이라면 다른 접근 방식을 고민해 보는 것이 좋다.
재귀 피보나치수열이 대표적 O(2ⁿ) 이다.
function fibonacci(n) {
if (n <= 1) {
return 1;
}
return fibonacci(n - 1) + fibonacci(n - 2);
}n >= 100 이면 평생 결과를 반환받지 못할 수도 있다.
| 데이터 크기 제한 | 예상되는시간 복잡도 |
|---|---|
| n ≤ 1,000,000 | O(n) or O (logn) |
| n ≤ 10,000 | O(n²) |
| n ≤ 500 | O(n³) |
입력 데이터가 클 때는 O(n) 혹은 O(log n)의 시간 복잡도를 만족할 수 있도록 예측해서 문제를 풀어야 하나 주어진 데이터가 작을 때는 시간 복잡도가 크더라도 문제를 풀어내는 것이 중요하다.