🔎 탐욕법 Greedy Algorithm
탐욕적 선택 속성(Greedy Choice Property) : 앞의 선택이 이후의 선택에 영향을 주지 않는다.
최적 부분 구조(Optimal Substructure) : 문제에 대한 최종 해결 방법은 부분 문제에 대한 최적 문제 해결 방법으로 구성된다.
예제) 거스름돈
🔎 동적 계획법 Dynamic Programming
Recursion + Memoization (재귀 + 메모제이션)
하위 문제의 해결책을 저장한 뒤, 동일한 하위 문제가 나왔을 경우 저장해놓은 해결책을 이용한다.
Memoization : 컴퓨터 프로그램이 동일한 계산을 반복해야 할 때, 이전에 계산한 값을 메모리에 저장함으로써 동일한 계산의 반복 수행을 제거하여 프로그램 실행 속도를 빠르게 하는 기술
예제) 피보나치수열
let memo = [];
function fibonacci(n){
if(n <= 1) return n
if(memo[n] !== undefined) return memo[n]
memo[n] = fibonacci(n -2) + fibonacci(n - 1)
return memo[n]
}🔎 순열과 조합
순열 permutation

n개의 원소를 가지는 집합에서 중복이 없고 r개의 원소를 선택하거나 순서대로 나열하는것 nPr
n은 원소의 총개수, r은 순서대로 나열 하려는 원소의개수 , P는 순열이라는 의미
3P2 순열식 코드
// n이 fruits 배열의길이(총개수), r은 반복문 중첩수(나열할 원소의개수)
function permutation(){
let fruits = ['🥝','🍓','🍏'];
let result = [];
for(let i =0; i < fruits.length; i++){
for(let j =0; j < fruits.length; j++){
if(i === j) continue;
result.push( [fruits[i], fruits[j]] )
}
}
return result
}
permutation()
// [ ['🥝', '🍓'],['🥝', '🍏'],['🍓', '🥝']
// ['🍓', '🍏'],['🍏', '🥝'],['🍏', '🍓'] ] // 6🔎 조합
중복 없이 순서에 상관없게 r개의 원소를 선택
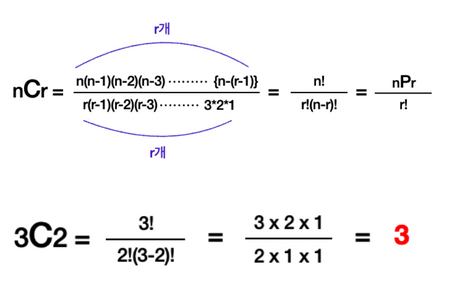
🔎 GCD와 LCM
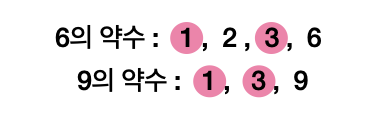
최대 공약수 Greatest Common Divisor
두 수 이상의 여러 수 중 공통된 약수를 의미한다. 여기서 약수(Divisor)는 어떤 수를 나누어떨어지게 하는 수이고 6,9는 3이 최대 공약수이다.
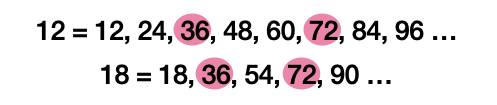
최소공배수 Lowest Common Multiple
두 수 이상의 여러 수 중 공통된 배수를 의미한다. 여기서 배수(Multiple)는 하나의 수에 정수를 곱한 수이고, 배수는 그 수에 의해 나누어 떨어지는 수이다. 또한 배수는 무수히 많아 최대 공배수는 구할 수 없다.
GCD LCM 을 쉽게 구하는식
유클리드 호제법
유클리드 호제법은 최대공약수와 관련이 깊은 공식이다. 2개의 자연수 a와 b가 있을 때, a를 b로 나눈 나머지를 r이라 하면 a와 b의 최대공약수는 b와 r의 최대공약수와 같다는 이론이다.
자연수 a와 b가 존재할 때, 해당 공식에 의거하여 계속해서 나누어 나가면 언젠가 나머지가 0인 상황이 도출이 되는데, 이때 나머지가 0이 되도록 나누는 수가 최대공약수이다.
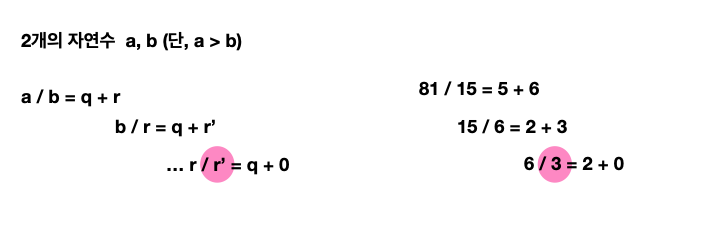
이 식은 a가 b보다 커야 한다는 조건(절대적 조건)이 있다.
q는 몫(Quotient)을 의미하고, r은 나머지(Rest)
// 유클리드 호제법을 이용해 최대공약수를 구하는 로직
function gcd(a, b){
while(b !== 0){
let r = a % b;
a = b;
b = r;
}
return a;
}
// 최소 공배수를 구하는 로직
function lcm(a, b){
return a * (b / gcd(a, b));
}🔎 Stack Queue
stack
stack은 데이터를 순서대로 쌓는 자료구조, 후입 선출로 동작, 입출력 방향이 같다.
스택의 크기가 제한되어 있으므로, 스택 오버플로(Stack Overflow) 에러가 발생하기도 한다.
배열의 PUSH , POP 메서드가 stack의 원리이고, 많은 데이터를 한번에 처리하지 않고 하나씩 처리한다.
const stack = [];
stack.push('🍌'); // ['🍌']
stack.push('🍓'); // ['🍌','🍓']
stack.push('🍒'); // ['🍌','🍓','🍒']
stack.push('🥝'); // ['🍌','🍓','🍒','🥝']
stack.pop(); // ['🍌','🍓','🍒']
stack.pop(); // ['🍌','🍓']
stack.pop(); // ['🍌',]
stack.pop(); // [](브라우저 뒤로가기,앞으로가기 버튼 클릭시 동작하는것도 스택의 원리)
queue
큐(Queue)는 줄을 서서 기다리다, 대기행렬 이라는 뜻으로, 스택과는 반대로 선입선출로 동작한다. 입출력 방향이 2개로, 다른 출입구를 가지며 앞의 데이터가 처리 될때까지 기다려야 한다.
PUSH,SHIFT 메서드
const queue = [];
queue.push('🍌'); // ['🍌']
queue.push('🍓'); // ['🍌','🍓']
queue.push('🍒'); // ['🍌','🍓','🍒']
queue.push('🥝'); // ['🍌','🍓','🍒','🥝']
queue.shift(); // ['🍓','🍒','🥝']
queue.shift(); // ['🍒','🥝']
queue.shift(); // ['🥝']
queue.shift(); // []🔎 트리 & 그래프
이진 트리(Binary tree)
자식 노드가 최대 두 개인 노드들로 구성된 트리이고, 왼쪽 자식 노드와 오른쪽 자식 노드로 나눌 수 있다.
자료의 삽입, 삭제 방법에 따라 정 이진 트리(Full binary tree), 완전 이진 트리(Complete binary tree), 포화 이진 트리(Perfect binary tree)로 나뉜다.
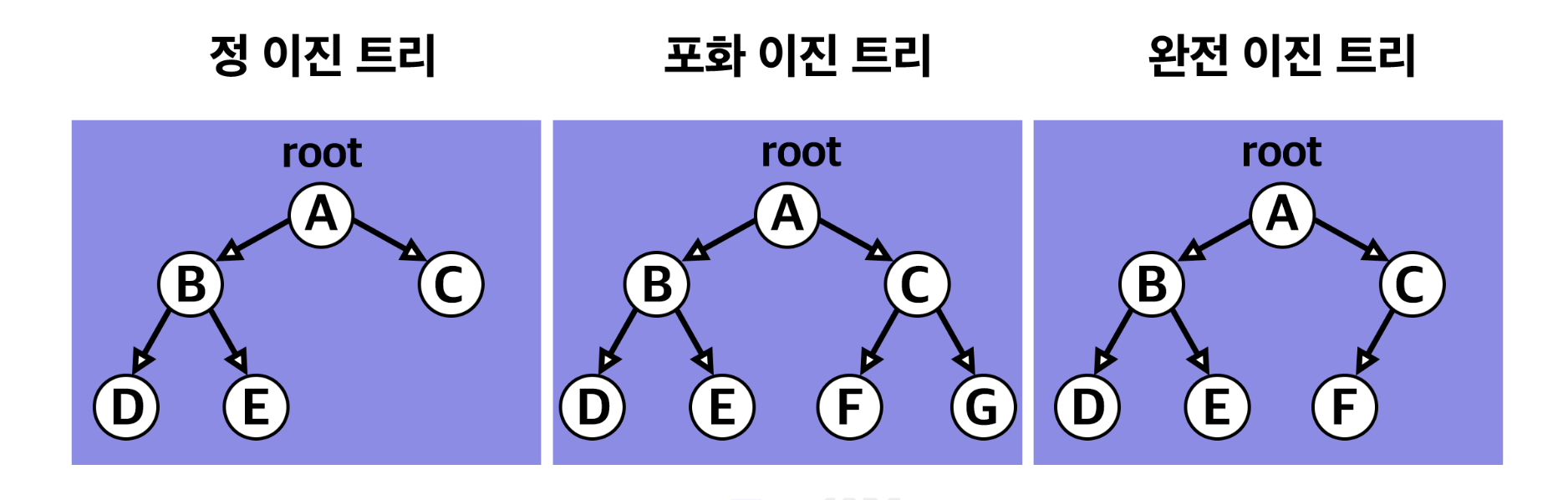
왼쪽 부터 탐색한다.
BFS(Breadth-First Search)
너비를 우선적으로 탐색하는 방법을 Breadth-First Search, 너비 우선 탐색이라 하고 주로 두 정점 사이의 최단 경로를 찾을 때 사용한다.
DFS(Depth-First Search)
깊이를 우선적으로 탐색하는 방법을 Depth-First Search, 깊이 우선 탐색이라한다.
BFS보다 탐색 시간은 조금 오래 걸릴지라도 모든 노드를 완전히 탐색할 수 있다.
그래프 Graph
여러개의 점들이 서로 복잡하게 연결되어 있는 관계를 표현한 자료구조