면접도 보고 잠시 휴식기를 좀 가졌읍니다... 맨날 쉬네
어쨌든 미루어 두었던 Flow Matching 논문으로 진행
Flow Matching이 Diffusion과는 다르지만 구현방식 자체에서는 큰 차이가 없어서 아마 기존에 diffusion 방식으로 학습/생성 하는 모델에 flow matching을 갈아끼우기만하는 식으로 구현자체는 어렵지 않고, 설명하겠지만 결국 효율을 확실히 개선하였고 안 쓸 이유를 딱히 모르긴 하겠다.. 그래서 아마 요즘 시대의 diffusion이라 하는 것들은 거의 Flow Matching이지 않을까 추측중

논문: https://arxiv.org/abs/2210.02747
코드: https://github.com/facebookresearch/flow_matching

Meta AI의 코드들이 프로젝트도 직관적이고 파이써닉한 문법을 신경써서 구성해가는 게 보여서 좀 선호한다 특히 테코도 열심히 잘짜줘서 ML모델 테코의 가이드라인을 잘 만들어주기도 하는 것 같다

---

Abstract 베끼기

본 논문은 Continuous Normalizing Flows(CNF)를 학습하는 새로운 패러다임을 제시하는 논문이다.
Flow Matching은 이 CNF를 확률 경로 상 벡터 필드에 대한 회귀를 통해 simulation-free 방식으로 학습한다.
요 확률 경로는 노이즈에서 데이터 샘플로 변환되는 다양한 가우시안 확률 경로와 호환되고, 기존 diffusion 경로들도 일반화될 수 있다.
diffusion 말고도 더 효율적으로 학습할 수 있는 확률 경로들도 존재한다.
결국 ImageNet 데이터셋을 가지고 성능을 더 잘 뽑을 수 있다.

내용을 알고보는 입장에서야 abstract의 요약은 가장 최선의 요약이었다 싶지만, abstract만 보고 넘길 수 있을만한 논문은 아니었을거같다..

기술 개요

Preliminaries: Continuous Normarlizing Flows

Flow Matching은 CNF 학습이기 때문에 알아야겠지?

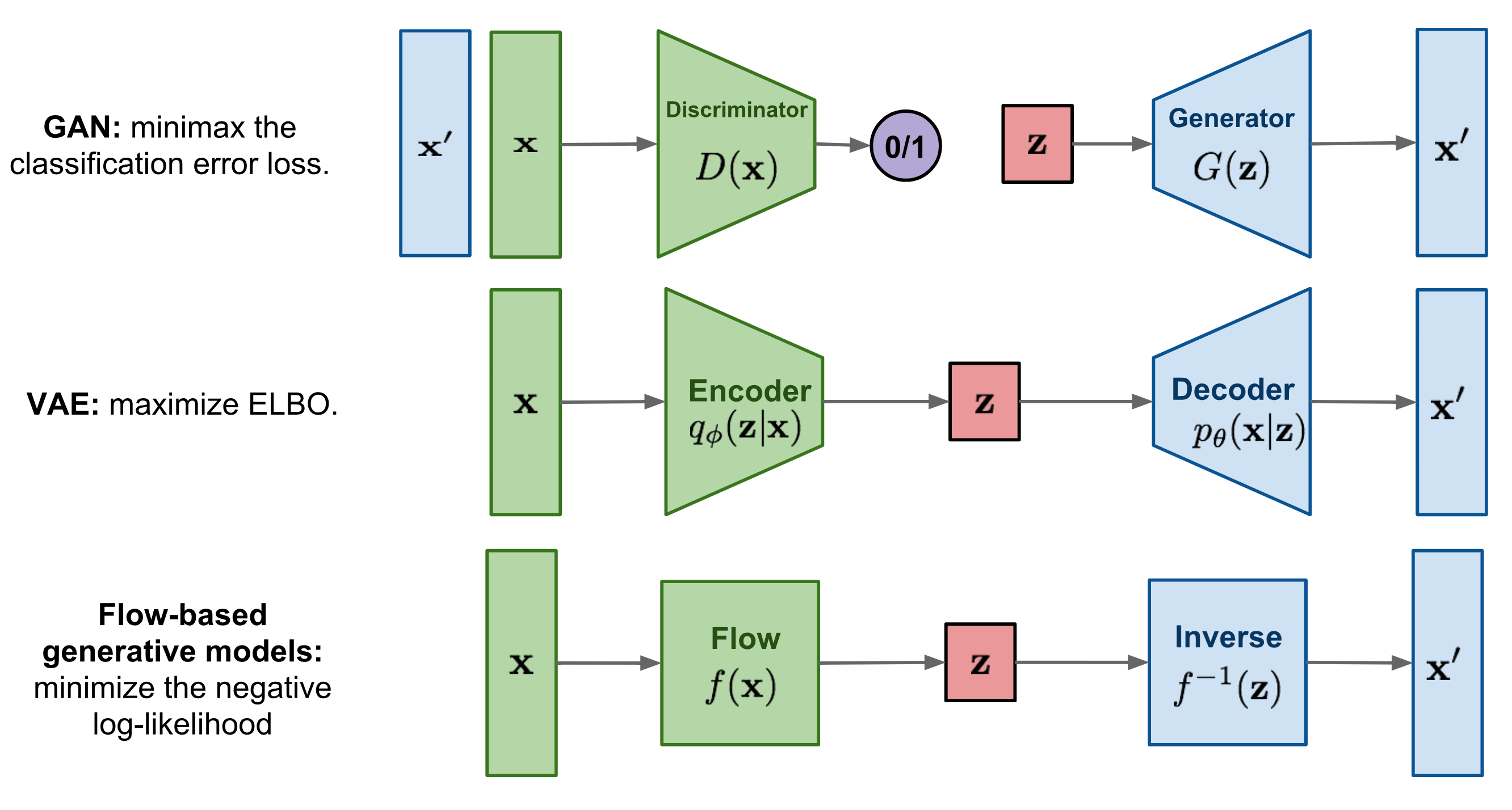
일단 continuous 조건 뗀 NF는 위 그림으로 그냥 간단하게 설명해볼 수 있다.
단순한 분포(예: Gaussian)를 복잡한 데이터 분포로 변환할 수 있는, 역변환 가능한 함수 구조를 설계하고 그 내부 파라미터를 학습하는 모델인거시다.

여기에 continuous 조건이 붙는다는건, 유한한 단계의 $f_1∘f_2∘... ∘ f_n$이 시간 개념을 포함하는 미분방정식이 되는건데, 그냥 수식을 보는게 편하다. 논문에서 CNF를 잘 가르쳐주고 있다.

데이터 공간 $\mathbb{R}^d$ 에 대하여 데이터 포인트 $x = (x_1, \dots, x_d) \in \mathbb{R}^d$를 가정

1. 확률 밀도 경로
$p : [0, 1] \times \mathbb{R}^d \rightarrow \mathbb{R}_{>0}$
이는 시간에 따라 변하는 확률 밀도 함수로, 다음 조건을 만족한다:

2. 시간에 따라 변하는 벡터 필드
$v : [0, 1] \times \mathbb{R}^d \rightarrow \mathbb{R}^d$

이 벡터 필드 $v_t$는 시간에 따라 변하는 diffeomorphism인 flow
$\phi : [0,1] \times \mathbb{R}^d \rightarrow \mathbb{R}^d$를 정의하는 데 사용되며,
다음과 같은 상미분방정식(ODE)에 의해 정의된다:

이 벡터 필드 $v_t$를 신경망 $v_t(x; \theta)$으로 모델링하여 이로부터 flow $\phi_t$의 deep parametric model이 정의되며, 이를 Continuous Normalizing Flow, CNF이라고 부른다.

블로그인만큼 좀 더 쉽게 설명하고 싶긴한데 더 쉽게 설명하는게 쉽지가 않구만
암튼 확률 경로의 흐름인 flow 자체를 모델링하는 것이 CNF이고, 이는 vector field를 학습하고 ode 문제를 푸는 방식으로 얻을 수 있다는 것이다

Flow Matching

Flow Matching(FM)의 목적은 초기 분포 $p_0 \sim \mathcal{N}(0,I)$에서 $p_1 \sim q$ 로 이어지는 목표 확률 경로를 잘 따라가는 벡터장을 학습하는 것이다.

그렇게 목표 확률 밀도 경로 $p_t(x)$와 그것을 생성하는 대응 벡터 필드 $u_t(x)$가 주어졌을 때,
Flow Matching(FM) 목적 함수는 다음과 같이 정의된다:

뭐 말로는 간단하지만 사실 $q$ 도 정확하게 모르고, $p_t$ 나 $u_t$의 closed-form의 식도 없는 상황이다. Flow Matching은 샘플 단위로 정의하고 이를 잘 모태놓아서 이 문제를 tractable한 문제로 전환하고자 한다.

marginal probability path와 vector field는 다음과 같이 정의될 수 있다.

그리고 이로부터 Theorem 1

조건부 확률 경로 $p_t(x \mid x_1)$를 생성하는 벡터 필드 $u_t(x \mid x_1)$들이 주어졌을 때, 임의의 데이터 분포 $q(x_1)$에 대해, marginal 벡터 필드 $u_t(x)$는 marginal 확률 경로 $p_t(x)$를 생성한다.
즉, $u_t$와 $p_t$는 연속 방정식 (continuity equation)을 만족한다.

예 솔직히 이해는 잘 못했습니다마는 결국 조건부 흐름으로 전체 흐름을 구성하여 문제를 해결할 수 있게 되었다는 것이다. 증명은 appendix를...

암튼 이것만으로도 적분 계산은 불가능하고, 여기서 내미는게 conditional flow matching (CFM) loss 이다.

그리고 Theorem 2
FM loss와 CFM loss 는 파라미터 $\theta$에 대해서 동일한 최적해를 가진다.

상당히 놀랍지만 증명까지 뒤적거리기는 귀찮아서 스킵할것이다.
아무튼 이제 CNF 문제를 푸는것은 조건부 확률 경로와 벡터필드만 가지고, 굉장히 간단한 loss를 통해 학습할 수 있게 되었다는 것이다.

Diffusion도 Flow Matching이다

논문에서도 설명을 수식 섞어가며 복잡하게 설명을 하고 있지만 이제 좀 기빨리고 술먹으러 갈거 같으므로 이해하고 있던 내용 기반으로 정성적으로 설명하자면

여태 설명한 Flow Matching을 간단하면서도 충분히 강력하게 구현할 수 있는게 Guassian Noise에서 실제 데이터로 가는 경로인 Gaussian Path이고, Diffusion에서 노이즈 예측해가며 없애는 이 과정 또한 하나의 확률 흐름 경로로 해석할 수 있다. 이 부분이 본 논문에서 잘 설명이 되어있다. 즉, FM을 diffusion 과정의 일반화된 형태로 볼 수 있다는 것이다.

이에 추가적으로 diffusion path는 결국 노이즈가 랜덤하게 추가되는 과정이기 때문에 샘플의 움직임 자체가 확률적인 텀을 포함한 SDE가 될 수 밖에 없는데, Flow Matching에서는 이를 ODE 문제로 단순화시켜버릴 수 있기 때문에, ODE solver를 활용하여 생성과정을 훨씬 간단하고 단순하게 수행할 수 있게 된다.

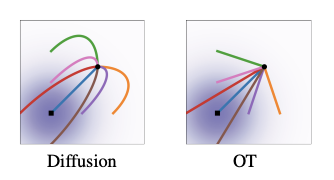
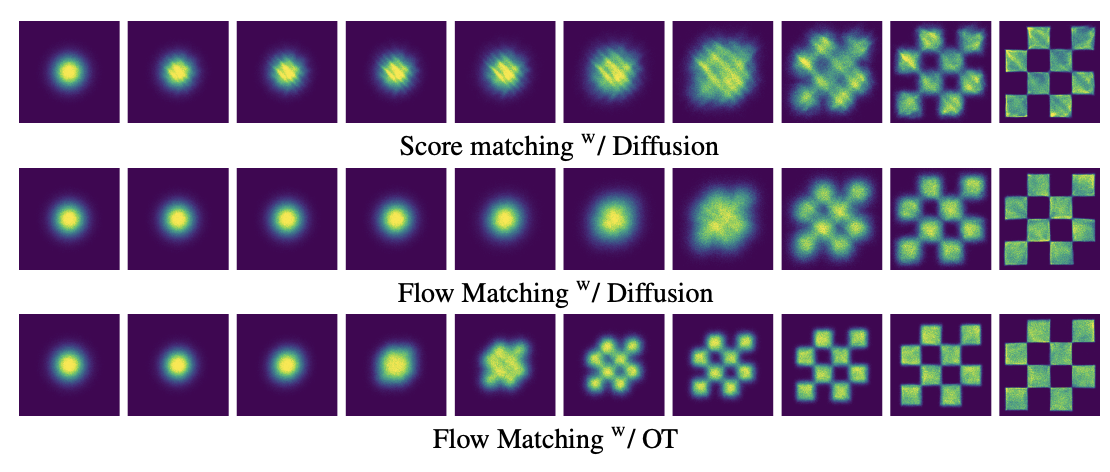
그리고 본 논문에서는 이렇게 확률경로 및 벡터 필드가 직선경로를 따르게 하여 훨씬 효율적으로 샘플링 수행을 할 수 있다고 보여준다.

---

논문을 처음 봤을때 벡터필드는 뭐고, 확률 경로는 뭐고,... 이런 CNF의 기본 용어들이 어려웠는데 논문 저자가 직접 말아주는 설명 유튜브를 보며 이해하는데 도움이 됐다
사실 저자 설명 자체가 도움이 된게 아니라 기가맥히게 설명을 도와주는 데이터 움직임 보여주는 ppt가 이해가 잘된다
소리끄고 봐도 이해될정도

https://www.youtube.com/watch?v=5ZSwYogAxYg&ab_channel=VantAI