상태를 알 경우 HMM 학습
HMM의 목적은 observation이 주어졌을 때 hidden state와 그 모델의 확률을 아는 것이다.
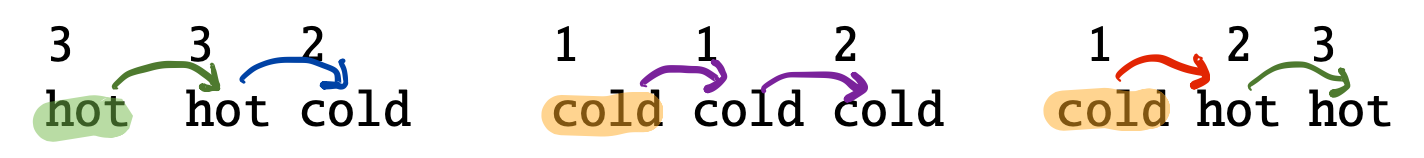
다음과 같이 observation이 전부 주어지고 그 때의 hidden state까지 모두 주어진다면 , 마코브 모델의 파라미터를 아는건 매우 쉽다.
우선 초기 확률을 구하자면 hot , cold , cold이므로
ㅠ(hot) = 1/3 , ㅠ(cold) = 2/3
전이 확률을 구하는 것도 간단하다. P(j|i)를 구하고자 할 때 전체 sequence에서 i에서 j로 가는 경우를 구하면 된다.
예를 들어 이전 state가 hot일 때 , 다음에 hot으로 변하는 경우는 3개중 2개이다.
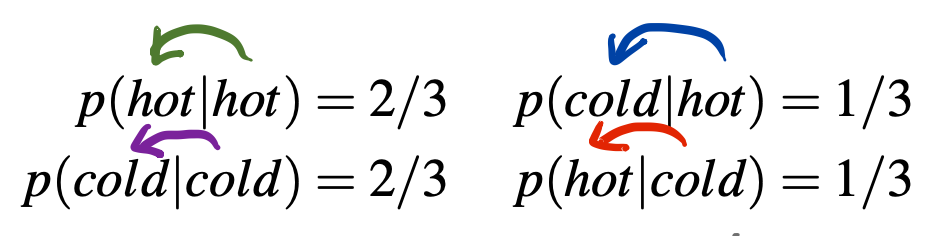
방출 확률도 그냥 세면 된다. hot에서 1,2,3이 나오는 경우를 각각 세면
0/1/3 이므로 각각 0, 1/4 , 3/4 이다.
상태를 모를 경우 HMM 학습
하지만 대부분의 경우 observation만 주어지고 hidden state까지는 정확히 알지 못한다. 이러한 상황에서 state 간의 방출,전이 확률을 알기 위해 expectation을 사용한다.

상태를 알 경우와 방식은 비슷하지만 expected number가 붙는 점이 다르다.
i에서 j로 전이할 expected number , j에서 Vk를 뱉을 expected number.
ξ 개념과 계산 과정
전이 확률과 관련한 ξ는 다음과 같이 계산한다
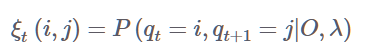
ξ(i,j)는 t일 때 i이고 , t+1일 때 j일 확률을 의미한다.
O는 주어진 sequenct , 감마는 파라미터이다.
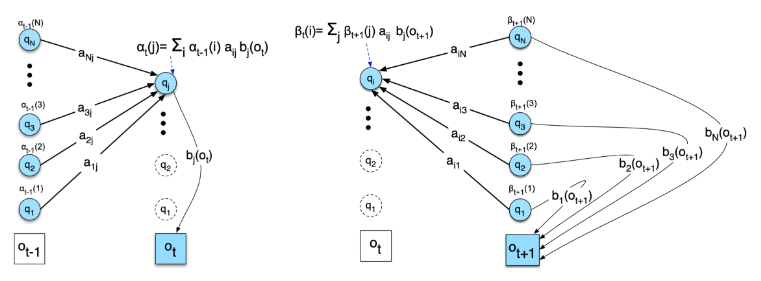
왼쪽 그림은 전방으로 t일 때 i일 확률을 구하는 것이다.
이전 state에 대한 확률과 전이 확률을 다 곱한 것이다.
오른쪽은 후방으로 t = j일 확률을 구하는 식이다.
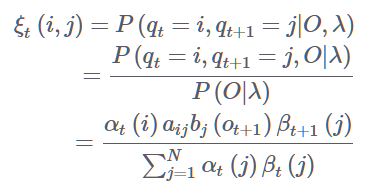
전방/후방을 이용해서 t,t+1에 i,j일 확률을 베이즈가 위 식이다.

이를 이용해서 i->j 에 대한 전이 확률의 식은 위와 같다.
γ와 방출 확률 계산하기
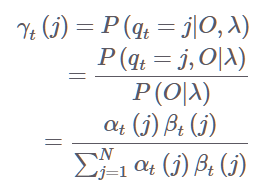
t번째 상태가 j일 확률은 다음과 같다. 분자는 j일 때의 전방,후방을 곱한 것이며 분모는 모든 state일 떄의 확률이다. 이를 기반으로 방출 확률을 계산하면

j일 때의 모든 경우가 분모이고 분자는 Vk를 return 하는 경우의 수이다.
Expectation Maximization algo.
이렇게 γ,ξ를 가지고 쉽게 전이,방출 확률을 추정할 수 있다.
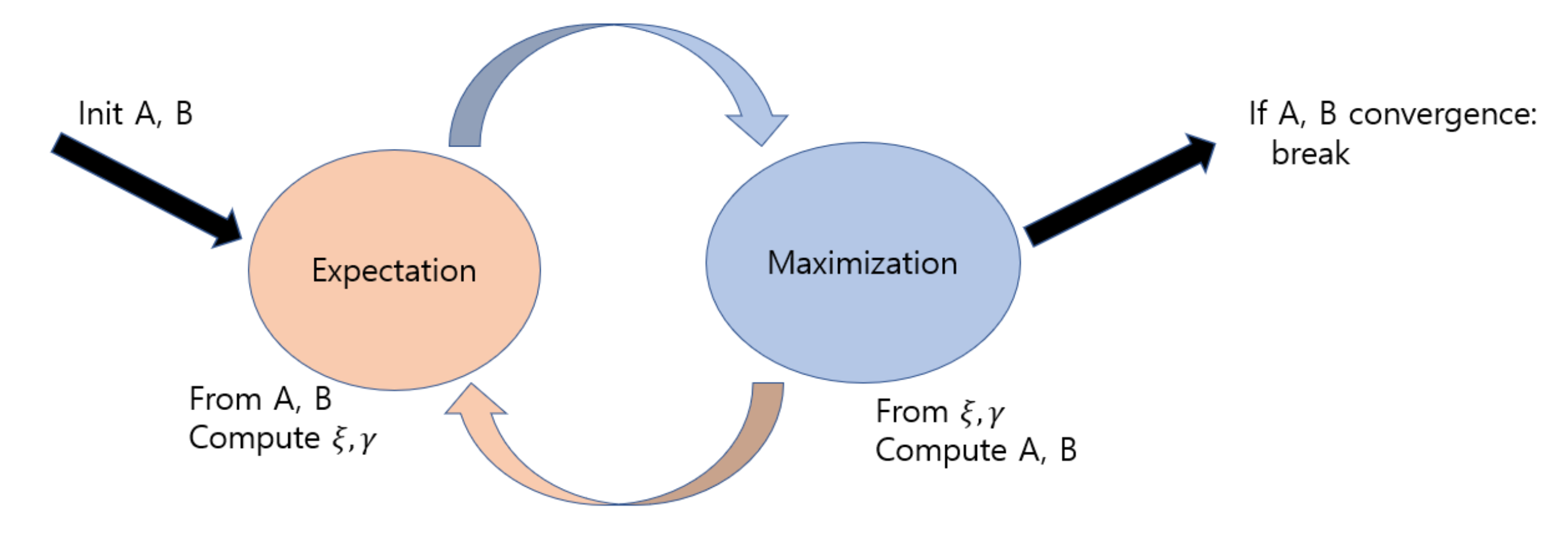
이를 구하기 위해 임의로 A,B(전이,방출 확률)을 초기화 하고
γ,ξ를 계산한다. γ,ξ를 구하면 역으로 A,B를 구한다. 이렇게 convergence 할 때까지 반복한다. A,B 초기화 값에 따라서 값이 많이 다르다.

Baum-Welch 의 수렴에 관한 증명
(이 알고리즘이 수렴하는 것에 대한 증명을 탐구하지만 , 본인 능력의 한계로 인해 할 수 있는 한 기록했다)
Baum-Welch 원문 (1970)
https://www.jstor.org/stable/pdf/2239727.pdf
해당 논문에서 baum-welch가 수렴하는 것에 대한 증명을 해놓았다 우선 notation부터 보면

i0부터 i(t)까지 이동할 확률은 다음과 같이 나타낼 수 있다
또한 다음 식에서 X는 sequence의 집합
x는 하나의 sequence (hidden state의 나열) 일 때
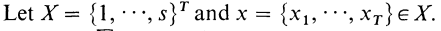
모든 sequence 중 하나가 나타날 확률은 다음과 같이 나타낼 수 있다
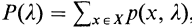
이때 x를 euclidian space에 매핑 시키면 식을 다음과 같이 변형 가능하다
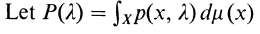
(u는 x를 실수로 매핑하는 함수)
한편 두 파라미터에 대한 엔트로피 식은 다음과 같다
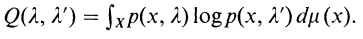
이때 다음과 같이 식을 전개할 수 있다
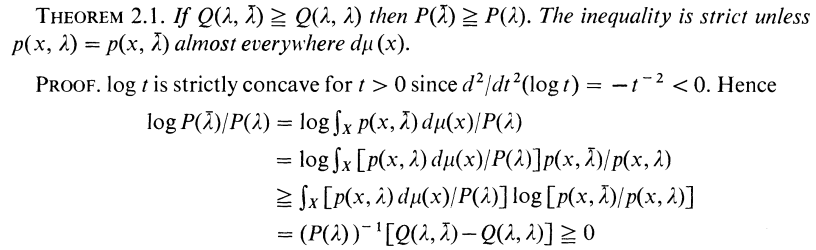
밑에 두번째에서 세번째 줄의 전개가 이해가 안갈 수 있는데 이는 단순히
를 미분하면 음수가 되어 감소함수임을 이용한 것으로 보인다.
그리고 마지막 줄은 위에서 나온 notation을 이용하면 전개할 수 있다. 이때 Q의 차이는 KL divergence이기 때문에 항상 양수이다. 따라서
이다.
따라서 일때 likelyhood는 같거나 증가한다.
...
쉽지 않네요.. 다시 돌아오겠습니다



깔끔한 정리! 잘 보고 갑니다