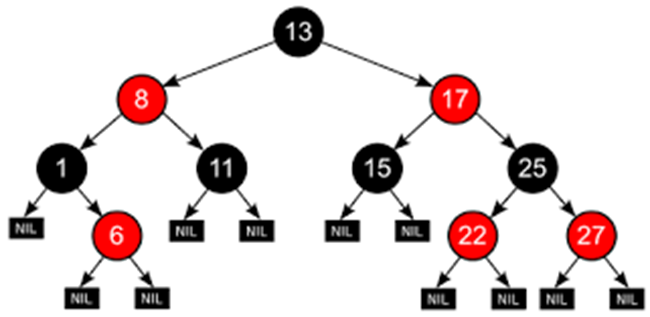
Red-Black 트리란 ❓
-
Red-Black 트리는 이진 탐색 트리의 단점을 보완하기 위하여 만들어진 균형잡힌 트리 중 하나이다.
-
이진 탐색 트리의 어떤 단점을 보완하기 위해 만들어졌을까?
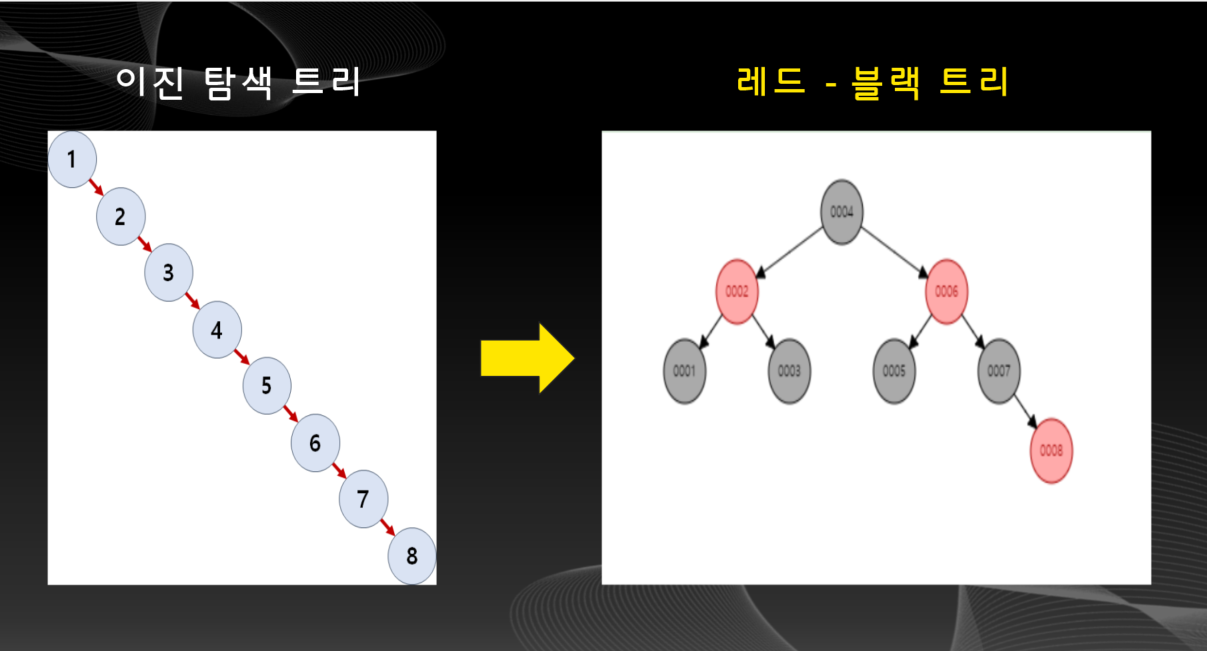
이진 탐색 트리에 예를 들어 "1, 2, 3, 4, 5, 6, 7, 8" 의 데이터를 넣었을 때 아래그림과 같이 오른쪽 방향으로, 일직선으로 트리가 그려지는 것을 볼 수 있을 것이다.하지만, 이렇게 되면 "8" 노드까지 가려면 루트 노드로부터 총 7번을 움직여야되는데 이것은 그냥 배열에 데이터를 넣고 값을 비교해가며 탐색하는것과 큰 차이가 없는 것을 알 수 있다.
-
위와 같이 이진 탐색 트리에선 7번을 이동하여 찾게되는 "8" 이라는 데이터를 레드 - 블랙 트리를 이용하면 3번만 이동하면 찾을 수 있다. 이처럼 데이터를 탐색하는데 있어서 훨씬 빠르고 효율적으로 탐색하는것이 가능해진다.
Red-Black 트리의 기본 규칙 ✍
-
모든 노드는 "빨간색" 혹은 "검은색" 이다.
-
루트 노드는 반드시 검은색 이다.
-
모든 노드들은 자식 노드로 리프 노드(NIL) 들을 가지고 있고, 리프 노드는 검은색이다.
( NIL : Null leaf, 자료를 갖지 않고 트리의 끝을 나타내는 코드 ) -
"빨간색" 노드의 자식은 "검은색"이다. 즉, "빨간색" 노드가 연속으로 나올 수 없다.
=> "빨간색" 노드가 연속으로 나오는 것을 "Double Red" 상황이 발생했다고 말한다.
-
모든 리프 노드에서 루트 노드까지 가는 경로에서 만나는 "검은색" 노드의 개수가 같다.
=> 이 조건때문에, 레드-블랙 트리에서는 데이터를 추가할 때 반드시 "빨간색"으로 \
추가한다.
🙊 Double Red 발생 시 해결방법
-
✅ 첫 번째, Recoloring
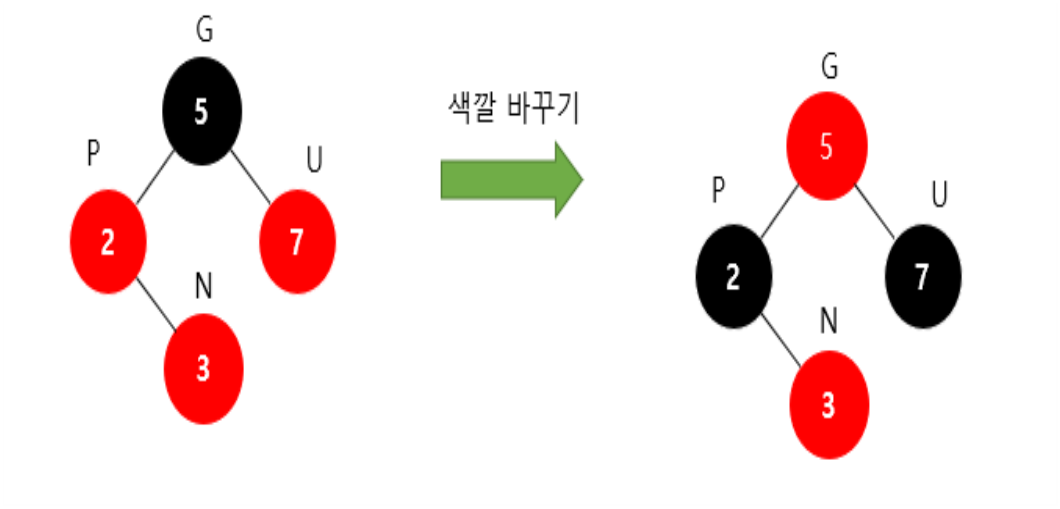
Recoloring은 새로 추가하는 노드의 삼촌이 빨간색일 때 실시하며, 새롭게 추가하는 노드(N) 의 부모(P) 와 삼촌(U) 을 검은색으로 바꾼 뒤, 새롭게 추가한 노드의 조부모(GP) 를 빨간색으로 바꿔주면 된다. -
이렇게만 보면, 정말 쉬워보인다고 생각할 수 있을 것이다. 왜냐하면, 트리의 구조를 바꾸는것이 아닌 노드들의 색깔만 규칙을 만족하도록 바꿔주면 되기 때문이다. 하지만 여기서 좋아하면 이 Recoloring의 달콤한 유혹에 빠지는 것이다.
-
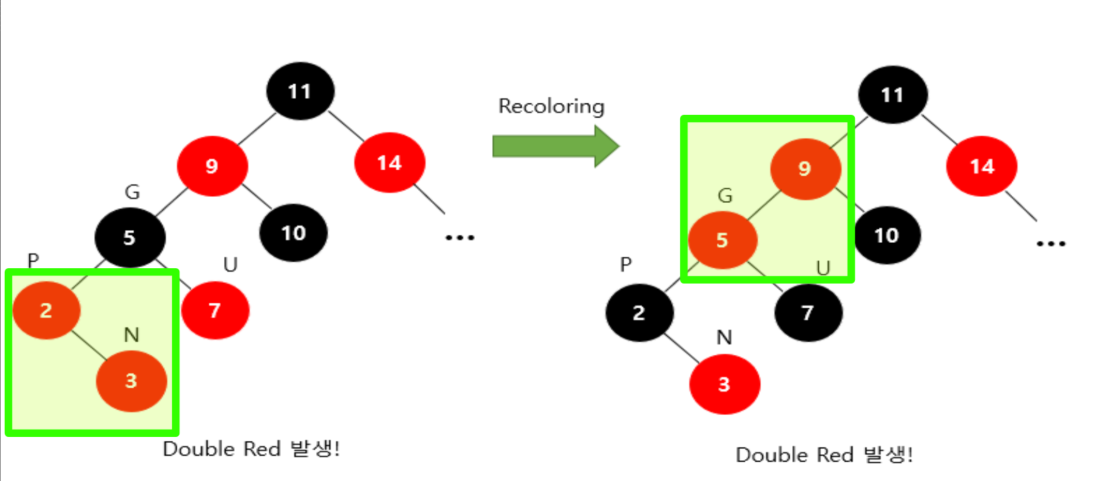
왜냐하면! Recoloring은 조부모(GP) 가 ROOT 라면 검은색으로 다시 바꿔줘야되고, 만약 조부모(GP)의 색깔을 빨간색으로 바꿔줬는데, 조부모의 부모가 빨간색이라면 또다시 Double Red 상황이 발생하기 때문이다.
따라서, Recoloring을 해준뒤에는 반드시 다시 확인하여 Double Red 가 아닌지 체크하고, 혹시나 Double Red 가 발생했다고 하면, 조건에 맞게 다시 Recoloring 또는 이어서 설명할 Restructuring 을 실시해줘야된다.
How Long? 바로 Double Red 가 발생하지 않을 때까지이다. -
아래는 Recoloring 동작 예시이다.
-
아래는 Recoloring 해준 뒤, 또다시 Double Red 가 발생한 예시이다.
-
✅ 두 번째, Restructuring
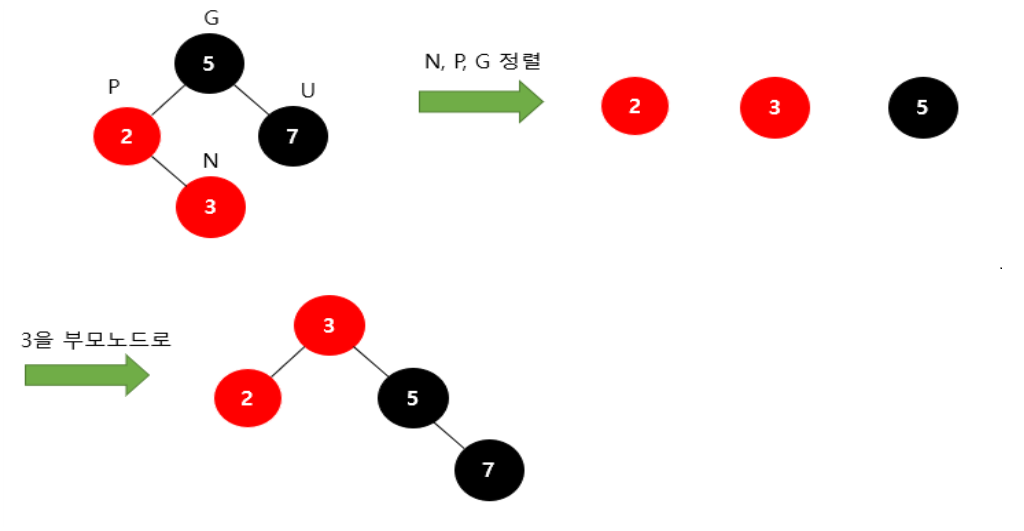
Restructuring이 정말 복잡하면서 중요한데, 그 이유는 말그대로 트리 자체를 재구조화 하기 때문이다. Restructuring은 새로 추가하는 노드(N) 의 삼촌(U) 이 검은색일때 실시하는 방법으로,새로 추가하는 노드(N), 부모(P), 조부모(GP) 를 오름차순으로 정렬한 뒤,
중간값(Middle) 을 부모 노드로 만들고,
작은값(Small) 을 부모 노드의 왼쪽 노드로 만들고,
큰값(Big) 을 부모 노드의 오른쪽 노드로 만들어서 재구성한다. -
그다음, Middle 노드를 검정색으로 바꾸고, 나머지 자식 노드들은 빨간색으로 바꾼다.
-
혹시나, 이런 생각을 할 수가 있다. 삼촌이 없는데 어떻게 해야되지?
이것은 위에서 설명한 레드-블랙 트리의 기본 규칙 중 3번째 항목을 보면 된다. 모든 노드들은 NIL 노드라는 검정색 노드를 자식 노드로 가지고 있다는 것을 다시 한번 알고 넘어가는 부분이다. -
아래는, Restructuring 동작 예시이다. Restructuring은 조부모의 노드를 검은색으로 만들기 때문에, Double Red 상황이 추가로 발생할 수는 없다.
-
하지만, Restructuring 을 위의 예시처럼 단순하게 생각해서 "오름차순 정렬한 다음에, 규칙대로 재구성해주면 되는거네" 라고 생각하면 크나큰 오산이다.
-
그 이유는 트리 구조 자체가 부모 노드와 자식 노드 간에는 쌍방향으로 연결되어 있는 상태이다. 이 상황에서, 트리의 구조 자체를 바꿔주기 위해서는 서로 연결되어 있는 쌍방향 연결들을 정확하게 다시 지정해줘야되는데,
이때 만약에 기존의 노드가 가지고 있는 수많은 자식 노드들은 어떻게 처리해야될지에 대한 의문이 발생할 것이다. 나는 이것을 정확히 파악하는데 정확히 2일이나 소요됬다.
-
우리가 Restructuring을 실시할 때 발생할 수 있는 상황은 총 4가지로 구분할 수 있다.
정확히 말하면 2가지인데, 왼쪽과 오른쪽으로 나눠지기 때문에 4가지라고 표현하였다. -
먼저 첫번째로, 아래와 같이 새로 추가하는 노드(N), 부모 노드(P), 조부모 노드(GP) 가 모두 일직선으로 나란히 구성되어 있는 상태이다. 이 경우에, 이미 일직선으로 구성되어 있다는 것 자체가 이진 탐색 트리에 의해 이미 오름차순으로 3개의 노드가 정렬되어 있다는 것을 확인할 수 있을 것이다.
따라서 이경우에는, 부모 노드(P)를 중심으로 왼쪽, 또는 오른쪽으로 회전시켜서 새롭게 노드를 구성해주면 끝난다. ( 아래 예시 참조 )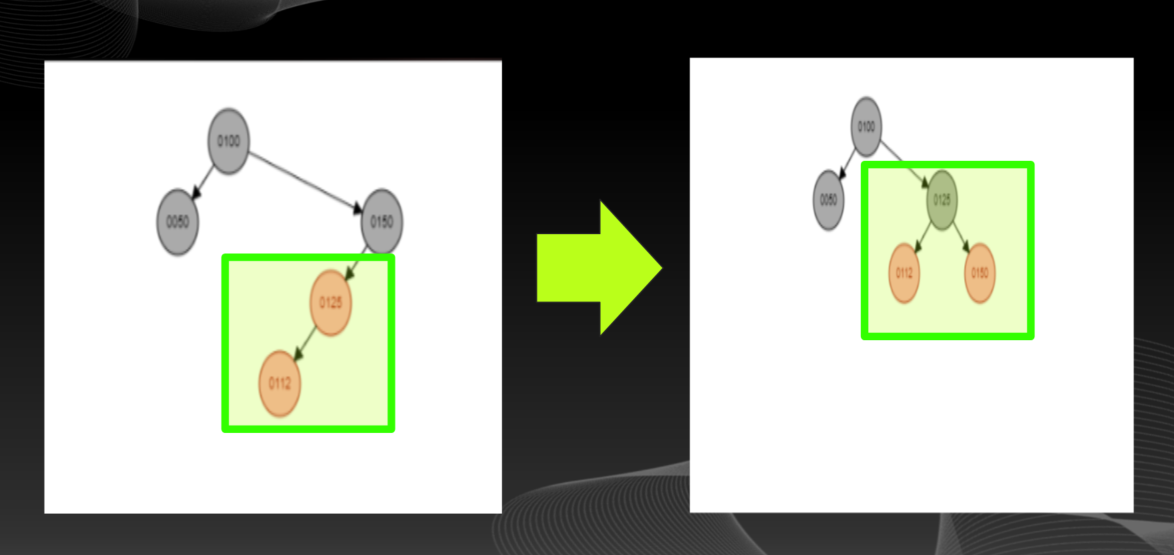
-
이렇게 일자로 구성이 되어있을때는, 단순히 회전만 해주면 되기 때문에 그나마 쉬워 보인다. 하지만! 다음번에 설명할 예시를 보면 정말 복잡하고 어렵구나라는 생각이 들 것이다.
그것은 바로, 새로 추가하는 노드(N), 부모 노드(P), 조부모 노드(GP) 가 조부모 노드로부터 오른쪽/왼쪽으로 내려온 뒤 거기서 부모 노드(P)의 왼쪽/오른쪽 노드에 새롭게 노드를 추가하는 상황이다.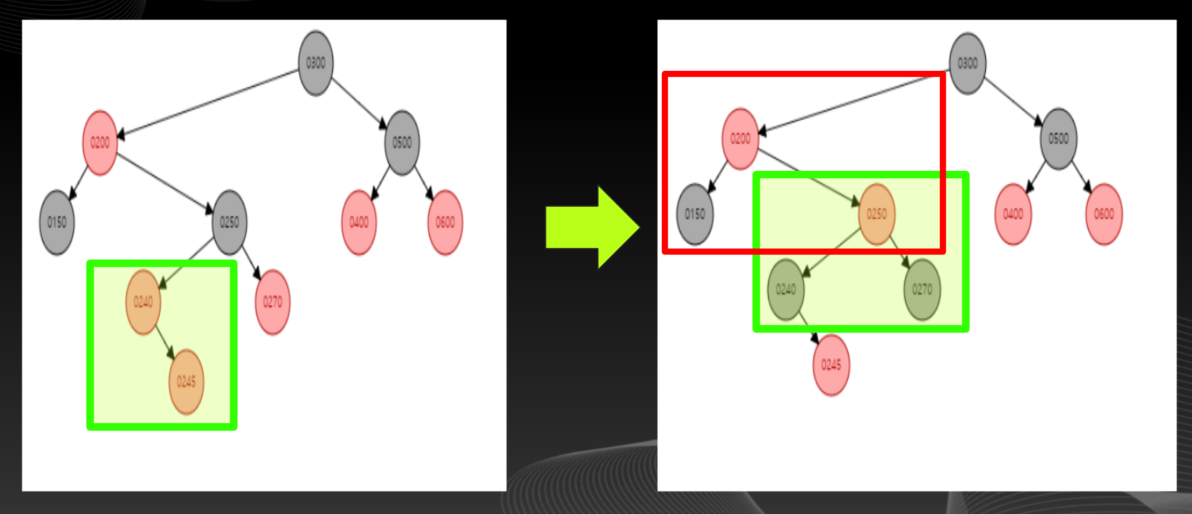
-
위의 그림을 보면
"245"의 데이터를 추가할때 Double Red 가 발생하여 Recoloring 을 실시해줬다. 하지만 Recoloring 실시 후 또다시 Double Red 가 발생하여 처리해주려고 보니 삼촌 노드인"500"노드가 검은색이기 때문에 Restructuring 을 해줘야 된다. -
이때, Restructuring 규칙대로라면
"250"노드가 중간값이기 때문에"200"노드와"300"노드의 중간으로 이동하여 부모 노드로 형성하고, 나머지 두 노드들을 자식 노드로 연결해줘야 되는 것이다. -
그러면
"250"노드의 자식 노드들은 어떻게 처리를 해줘야 될까? 이것이 핵심인 것이다.
그것은 바로,"250"노드보다 작은 왼쪽 자식 노드들은"200"노드보다는 크기 때문에"200"노드의 오른쪽 자식 노드로 연결시켜준다.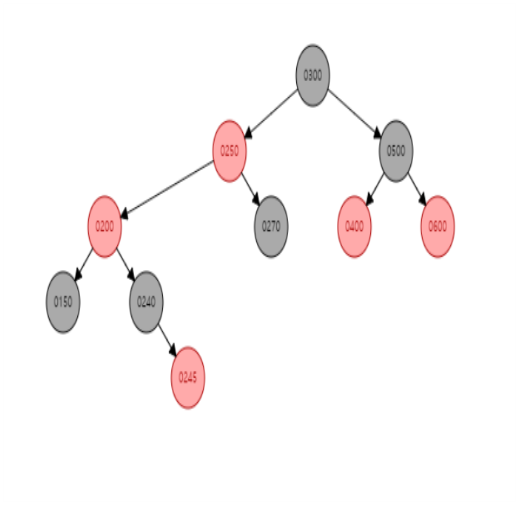
-
위와 같이
"250"의 왼쪽 자식들은"200"노드의 오른쪽 자식으로 연결시켜주고,"250"노드는"200"과"300"의 중간으로 들어간 것을 볼 수 있다.여기서, 그럼 또다시
"250"노드의 오른쪽 자식인"270"노드는 어떻게 처리해야 될까? 라는 의문이 생길 것이다.
그것은,"250"노드보다는 크지만"300"노드보다는 작으므로"300"노드의 왼쪽 자식으로 연결되는 것이다.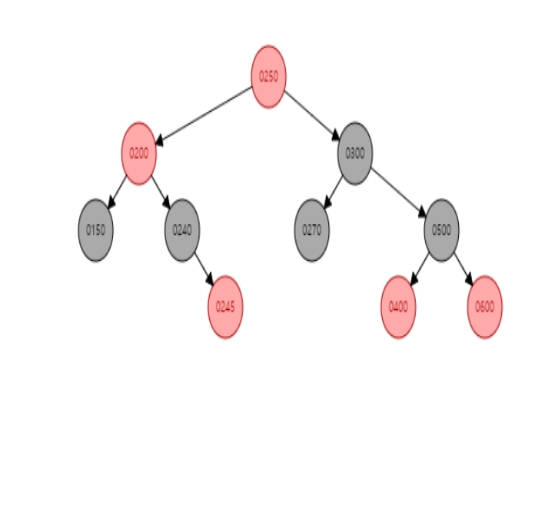
-
그렇게 하여, Restructuring 을 해주면 위와 같이 되는데, 여기서
"250"노드가 root 노드이기 때문에, 마지막으로"250"노드를 검은색으로 바꿔주면 아래와 같이 최종적으로 레드-블랙 트리의 규칙을 만족토록 트리가 형성된 것을 볼 수있다.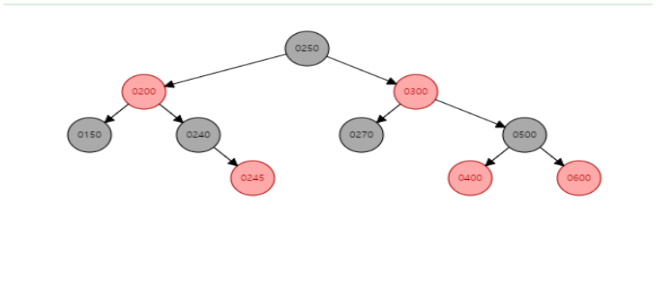
-
이처럼, Restructuring 을 한다는 것은 기존에 연결되어 있던 트리의 구조 자체를 전부 바꿔서 새로 연결해줘야되기 때문에 중요한 것이다.
💻 Red-Black 트리 코드로 구현하기
- 위에서 학습한 개념을 바탕으로, Red-Black 트리를 자바 코드로 아래와 같이 구현해봤다.
// ✅ Node 클래스
public class Node implements TreePrinter.PrintableNode{
Integer data;
Node left; // 왼쪽 자식 노드
Node right; // 오른쪽 자식 노드
Node parent; // 부모 노드
boolean color = true; // 색깔 지정 (true : 빨간색 / false : 검은색)
// Node를 생성할때 매개변수로 노드에 들어갈 데이터와,
// 해당 노드의 부모 노드를 포함하여 생성한다.
// 그 이유는, Double Red 문제가 발생한 노드의 삼촌 노드를 쉽게 찾아가기 위해서이다.
// 이렇게 하면, 삼촌 노드는 해당 노드의 부모님의 부모님을 찾아간 뒤
// 조부모의 왼쪽, 또는 오른쪽 자식노드가 삼촌 노드라는 것을 알 수 있다.
public Node(Integer data,Node parent) {
this.data = data;
this.parent=parent;
// 모든 노드를 생성할때 노드의 자식 노드로 NIL 노드를 생성해준다.
if(data != null){
left = new Node(null,this);
left.color = false;
right = new Node(null,this);
right.color = false;
}
}
// 여기부터는 출력을 그림으로 출력하기 위한 코드
@Override
public TreePrinter.PrintableNode getLeft() {
return this.left;
}
@Override
public TreePrinter.PrintableNode getRight() {
return this.right;
}
@Override
public String getText() {
return "["+data+"]" +"[" + color + "]";
}
// 여기까지
}// ✅ Red-Black 트리 클래스
import redblack2.Node;
public class RedBlackTree {
Node root; // root 노드 변수를 생성한다.
public RedBlackTree() {
//this.root = root;
}
// ✅ 이진탐색 트리 의거 데이터를 추가하는 기능 add 메서드
public void add(Integer data){
// 만약 root가 null 이라면
if(root == null){
// 새로 추가하는 데이터를 root 노드의 데이터로 넣어준다. 이때 root 노드의 부모는 null 이다.
root = new Node(data,null);
// root 노드의 색깔은 검정색이므로 검정색으로 설정해준다.
root.color = false;
// 다시 메서드의 처음으로 돌아간다.
return;
}
// 새로운 "node" 라는 이름의 노드 객체 변수를 생성 하고, "node" 변수에 "root" 를 저장해준다.
Node node = root;
// 무한 반복을 실시한다.
while(true){
// 만약 기존에 생성한 "node" 변수의 데이터가 새로 삽입하는 노드의 데이터보다 작으면
if(node.data < data){
// 만약 기존에 생성한 "node" 변수의 오른쪽 노드에 데이터(값) 이 없다면(null 이라면)
if(node.right.data == null){
// 기존 "node"의 오른쪽에 새로운 노드를 생성하여 연결해준다.
node.right = new Node(data,node);
// 기준이 되는 "node"의 위치를 기준 노드의 오른쪽 노드로 이동하여 기준 노드를 변경한다.
node = node.right;
// 반복문을 종료시킨다(왜? 새로운 노드를 생성하였기 때문이다.)
break;
}
// 만약 기준 노드의 오른쪽이 null이 아닐때는 기준 노드의 위치를 오른쪽 노드로 이동시켜준다.
// 그리고 나서 오른쪽으로 이동한 노드의 위치에서 다시 반복문을 처음부터 시작한다.
node = node.right;
}
// 그렇지 않고 만약에 기존에 생성한 "node" 변수의 데이터가 새로 삽입하는 노드의 데이터보다 크다면
else{
// 만약 기존에 생성한 "node" 변수의 왼쪽 노드에 데이터(값) 이 없다면(null 이라면)
if(node.left.data == null) {
// 기존 "node"의 왼쪽에 새로운 노드를 생성하여 연결해준다.
node.left = new Node(data,node);
// 기준이 되는 "node"의 위치를 기준 노드의 왼쪽 노드로 이동하여 기준 노드를 변경한다.
node = node.left;
// 반복문을 종료시킨다(왜? 새로운 노드를 생성하였기 때문이다.)
break;
}
// 만약 기준 노드의 왼쪽이 null이 아닐때는 기준 노드의 위치를 왼쪽 노드로 이동시켜준다.
// 그리고 나서 왼쪽으로 이동한 노드의 위치에서 다시 반복문을 처음부터 시작한다.
node = node.left;
}
}
// 만약 기준으로 잡은 "node" 의 부모의 색깔이 검정색이라면 반복문을 탈출한다.
// Why ? -> 규칙을 만족하는지 더이상 확인할 필요가 없다. 더블레드 조건이 발생할 일이 없기 때문에
if(!node.parent.color) return;
// 위에서 이진 탐색 트리 의거 데이터의 삽입이 이뤄졌다.
// 이것을 레드블랙 트리 규칙을 만족하는지 아래의 반복문으로 점검해주겠다.
// 레드블랙트리의 규칙을 만족할때까지 무한 반복한다.
while(!isCompelet() ){
// 만약 기준 node의 조부모가 null 이라면 반복문을 탈출한다. 왜? 조부모가 null이라는것은 root이기 때문에
if(node.parent.parent == null) break;
// 삼촌 노드 변수를 새로 생성하는데 삼촌 노드를 "기준 노드의 조부모의 오른쪽" 이라고 저장할 때,
Node uncle = node.parent.parent.right;
// 만약 삼촌이 기준 노드의 부모와 같다면 삼촌은 조부모의 오른쪽이 아니기 때문에,
if(uncle == node.parent){
// 삼촌 노드를 "기준 노드의 조부모의 왼쪽" 으로 다시 저장해준다.
uncle = uncle.parent.left;
}
// 만약 삼촌 노드의 색깔이 참이라면(빨간색 이라면)
if(uncle.color){
// recoloring() 메서드를 실시하는데 실시한 뒤 반환된 "node"를 "node 변수" 에 저장해준다.
node = recoloring(node);
// root 노드의 색깔은 검정색으로 저장해준다.
// Why? recoloring 과정에서 만약, root 노드까지 올라갔을때 root 노드의 색깔을 빨간색으로 바꾸기 때문에
root.color = false;
}
// 그렇지 않고 만약에 삼촌 노드의 색깔이 거짓이라면(검정색 이라면)
else{
// restructruing() 메서드를 실시하는데 실시한 뒤 반환된 "node"를 "node 변수" 에 저장해준다.
node = restructuring(node);
}
// 만약 위의 조건문을 통해 나온 "node 변수" 의 부모가 null 이라면 반복문을 탈출한다.
if(node.parent == null) break;
}
}
// ✅ recoloring 기능의 메서드를 생성한다.
private Node recoloring(Node node) {
// 삼촌 노드를 기준 노드의 조부모의 오른쪽이라고 가정하여 저장할 때,
Node uncle = node.parent.parent.right;
// 만약 삼촌 노드가 기준 노드의 부모와 같다면
// 삼촌 노드를 "조부모의 왼쪽" 으로 다시 저장해준다.
if(uncle == node.parent) {
uncle = uncle.parent.left;
}
// 삼촌 노드의 색깔은 검정색으로 바꾸고,
uncle.color = false;
// 기준 노드의 부모의 색깔을 검정색으로 바꾸고,
node.parent.color = false;
// 기준 노드의 조부모의 색깔을 빨간색으로 바꿔준다.
node.parent.parent.color = true;
// 이때 root의 색깔을 건들 수 있으므로 root 의 색깔은 검정색으로 설정해준다.
root.color = false;
// 기준 노드의 조부모를 node 매개변수로 반환 시켜준다.
// 왜? 기준 노드의 조부모가 빨간색으로 바뀌면서 또다시 더블레드 문제가 발생할 수 있기 때문에
return node.parent.parent;
}
// ✅ restructuring 기능 구현 메서드 생성
private Node restructuring(Node node) {
Node big; // 가장 큰 값의 노드 변수를 "big" 으로 생성
Node middle; // 가장 중간 값의 노드 변수를 "middle" 으로 생성
Node small; // 가장 가장 작은 값의 노드 변수를 "small" 으로 생성
// 만약 매개변수로 들어온 "node" 가 "node"의 부모의 왼쪽에 있다면
if(node == node.parent.left){
// 만약 "node" 의 부모가 "node" 의 조부모의 왼쪽에 있다면 (왼쪽으로 일직선 형태)
if(node.parent == node.parent.parent.left){
// "big" 노드는 "node" 의 조부모가 되고
big = node.parent.parent;
// "middle" 노드는 "node" 의 부모가 되고
middle = node.parent;
// "small" 노드는 "node" 가 된다.
small = node;
}
// 그렇지 않고 만약에, "node"의 부모가 "node"의 조부모의 오른쪽에 잇다면 (오른쪽으로 나오다가 왼쪽으로 꺾이는 형태)
else{
// "big" 노드는 "node" 의 부모가 되고
big = node.parent;
// "middle" 노드는 "node" 가 되고
middle = node;
// "small" 노드는 "node"의 조부모가 된다.
small = node.parent.parent;
}
}
// 그렇지 않고 만약 매개변수로 들어온 "node" 가 "node"의 부모의 오른쪽에 있다면
else{
// 만약 "node" 의 부모가 "node" 의 조부모의 왼쪽에 있다면 (왼쪽으로 나오다가 오른쪽으로 꺾이는 형태)
if(node.parent == node.parent.parent.left){
// "big" 노드는 "node" 의 조부모가 되고
big = node.parent.parent;
// "middle" 노드는 "node" 가 되고
middle = node;
// "small" 노드는 "node"의 부모가 된다.
small = node.parent;
}
// 그렇지 않고 만약에 "node" 의 부모가 "node" 의 조부모의 오른쪽에 있다면 (오른쪽으로 일직선 형태)
else{
// "big" 노드는 "노드의 조부모가 되고
big = node;
// "middle" 노드는 "node" 의 부모가 되고
middle = node.parent;
// "small" 노드는 "node"의 조부모가 된다.
small = node.parent.parent;
}
}
// 여기까지해서 해서 "big", "middle", "small" 노드가 정해졌다.
// 만약 "node" 의 조부모의 부모가 null 이라면
if(node.parent.parent.parent == null) {
// root를 "middle"로 저장해주고
this.root = middle;
// 그렇지 않고 만약 "node"의 조부모의 부모가 null 이 아니라면
} else {
// 만약, "node"의 조부모가, 조부모의 부모의 왼쪽 노드라면
if(node.parent.parent == node.parent.parent.parent.left) {
// "node"의 조부모의 왼쪽 노드로 "middle" 을 연결해주고,
node.parent.parent.parent.left = middle;
// 그렇지 않으면
} else {
// "node"의 조부모의 오른쪽 노드로 "middle" 을 연결해준다.
node.parent.parent.parent.right = middle;
}
}
// "middle" 노드의 부모는 기존 "node"의 조부모의 부모로 저장한다.
middle.parent = node.parent.parent.parent;
// 만약, "middle" 노드의 부모가 null 이라면 middle이 root라는게 되므로 root에 middel을 설정해준다.
if(middle.parent == null) this.root = middle;
// 만약, "small" 노드가 "middle" 노드의 왼쪽이 아니라면
if(small != middle.left){
// "middle" 노드의 왼쪽의 부모를 "small"로 저장하고
middle.left.parent = small;
// "small" 노드의 오른쪽을 "middle" 노드의 왼쪽으로 저장하고
small.right = middle.left;
// "middle" 노드의 왼쪽을 "small" 노드로 저장하고
middle.left = small;
// "small" 노드의 부모를 "middle" 노드로 저장한다.
small.parent = middle;
}
// 만약, "big" 노드가 "middle" 노드의 오른쪽이 아니라면
if(big != middle.right){
// "middle" 노드의 오른쪽의 부모를 "big"으로 저장하고
middle.right.parent = big;
// "big" 노드의 왼쪽을 "middle" 노드의 오른쪽으로 저장하고
big.left = middle.right;
// "middle" 노드의 오른쪽을 "big" 노드로 저장하고
middle.right = big;
// "big" 노드의 부모를 "middle" 노드로 저장한다.
big.parent = middle;
}
// "middle" 노드의 색깔은 검정색으로 저장하고
middle.color = false;
// "middle" 노드의 왼쪽과 오른쪽 노드의 색깔은 빨간색으로 저장한다.
middle.left.color = true;
middle.right.color =true;
// "middle" 노드를 반환한다.
return middle;
}
// ✅ 레드-블랙 트리 규칙을 만족하는지 확인하기 위한 메서드
private boolean isCompelet() {
return this.findDoubleRedBypreOrder();
}
// ✅ 여기부터 Double Red 상황이 발생하는 노드를 찾기위한 전위 순회 메서드
private Boolean findDoubleRedBypreOrder() {
Node node = this.root;
Boolean result = false;
findDoubleRedBypreOrder(node.left,result);
findDoubleRedBypreOrder(node.right,result);
return result;
}
private void findDoubleRedBypreOrder(Node node,Boolean isDoubleRed) {
if(node.data == null) return;
if(node.color){
if(node.left.color) {
isDoubleRed=true;
return ;
}
if(node.right.color) {
isDoubleRed=true;
return ;
}
}
findDoubleRedBypreOrder(node.left,isDoubleRed);
findDoubleRedBypreOrder(node.right,isDoubleRed);
}
// 여기까지
}// ✅ Main 클래스
public class RedBlackTreeMain {
public static void main(String[] args) {
RedBlackTree rbt = new RedBlackTree();
rbt.add(20);
rbt.add(30);
rbt.add(40);
rbt.add(50);
rbt.add(25);
rbt.add(37);
TreePrinter.print(rbt.root); // 출력
}
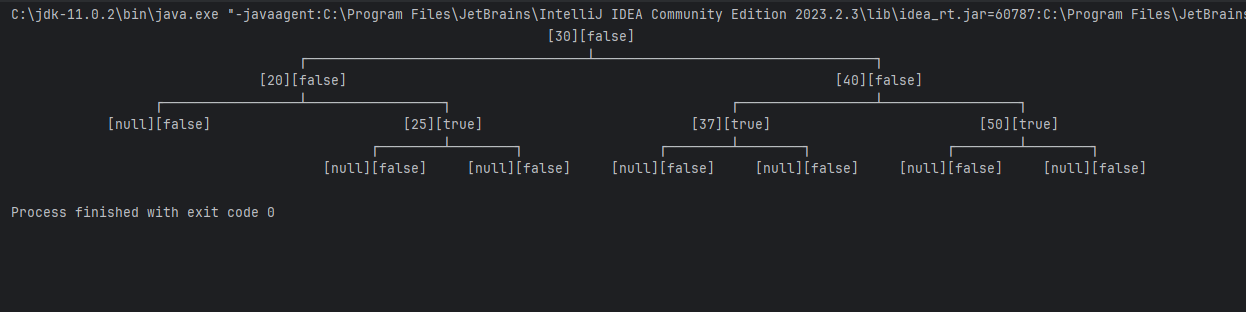
}
-
출력하면 위의 그림과 같은 결과가 출력되는 것을 확인할 수 있을 것이다.
-
코드로 구현하는데 있어서 가장 어려웠던 점은, Restructuring 을 구현해 내는 것이었다. 모든 연결 고리들을 완전히 새롭게 연결을 해줘야되는데, 이때 쌍방향 연결을 정확하게 설정해주지 않으면 트리가 정상적으로 동작하지 않기 때문이다.
-
또하나 중요한 것은 가장 많이 떴던 오류가 Null Pointer Exception 이었는데, 이것은 왜냐하면 root 노드의 부모는 null 값이기 때문이다. 트리의 아래서부터 root 까지 올라갈때 이 부분을 별도로 안적어주면 해당 오류가 뜰 것이다.
자료구조 느낀점 👀
-
어제부터 오늘까지, 팀별로 각자 3가지 자료구조 ( B-Tree / AVL Tree / Red-Black Tree ) 를 구현해보고 발표하는 시간을 가졌다. 처음 Red-Black 트리를 담당하게 되고 나서 단순하게만 생각했더니 너무도 쉽다고 생각했다.
-
하지만, 파고들면 파고들수록 발생할 수 있는 상황이 많이 있다는 것을 깨닫고 Restructuring 을 정확히 이해하는데만 꼬박 2일 걸린 것이다.
-
이제는 완벽하게 이해하여 누군가에게 설명을 해야된다면 설명할 수 있는 수준으로 숙지를 하였는데, 중요한 것은 개념도 개념이지만 내가 생각한 것을 코드로 구현하는 것인것 같다.
-
위의 코드도 우리조의 팀장님께서 도움을 많이 주셔서 완성시킬 수 있었는데, 아직 나스스로 처음부터 끝까지 작성하는 것은 무리가 있는 것 같다. 그렇기에 더더욱 끊임없이 노력을 해야겠다고 생각이 들었고, 내일부터 시작하는 알고리즘 수업도 열심히 듣고 코드로 구현해볼 예정이다. 😎
