Heap 이란❓
-
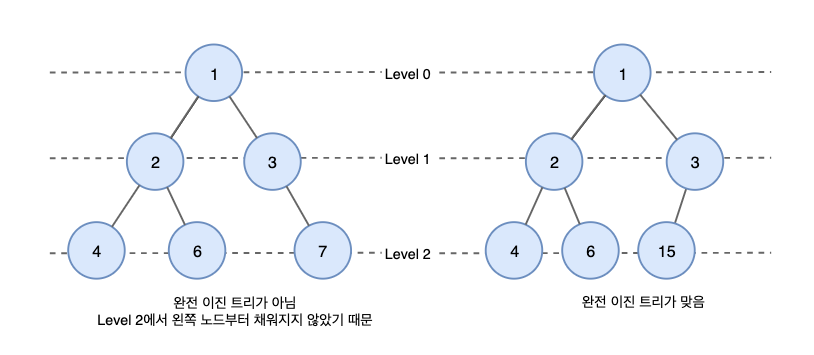
힙은 여러개의 값들 중에서 최대값 또는 최솟값을 찾아내는 연산을 빠르게 하기 위해 고안된 완전 이진 트리를 기본으로 한 자료구조이다.
➡ 완전 이진 트리 : 마지막 레벨을 제외한 모든 노드에서 자식들이 꽉 채워진 이진 트리
-
힙은 반정렬 상태를 유지한다.
➡ 반정렬 상태 : 부모 노드와 자식 노드 간의 관계만 신경쓰고, 형제 간의 우선 순위는
고려하지 않는 상태
-
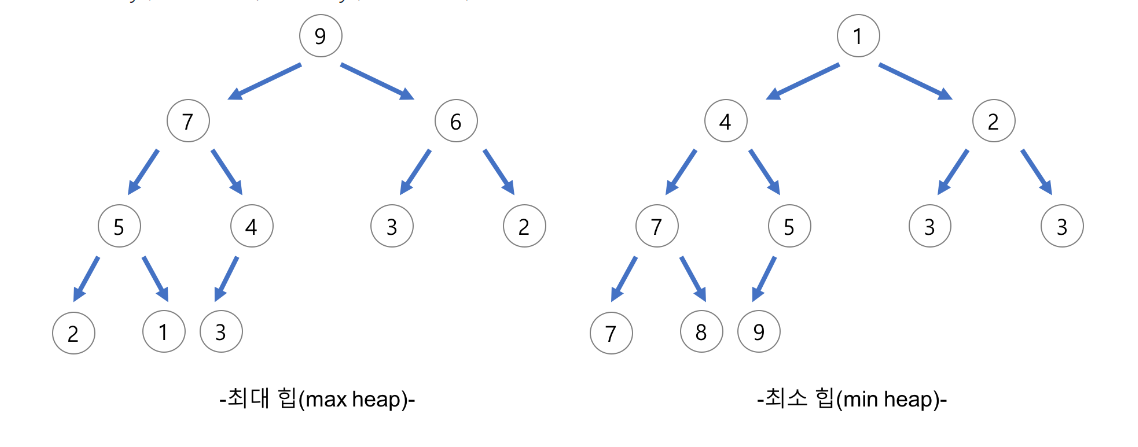
힙의 종류
1) 최대 힙 : 부모 노드의 값이 자식 노드의 값보다 크거나 같음
2) 최소 힙 : 부모 노드의 값이 자식 노드의 값보다 작거나 같음
-
힙의 구현
➡ 힙을 저장하는 표준적인 자료구조는 배열이다.
➡ 구현을 쉽게 하기 위하여 배열의 첫번째 인덱스(0번) 은 사용하지 않는다.
➡ 특정 위치의 노드 번호는 새로운 노드가 추가되어도 변하지 않는다.
➡ 부모 노드와 자식 노드의 관계
- 부모 인덱스 = 자식 인덱스 / 2
- 왼쪽 자식 인덱스 = 부모 인덱스 2
- 오른쪽 자식 인덱스 = (부모 인덱스 2) + 1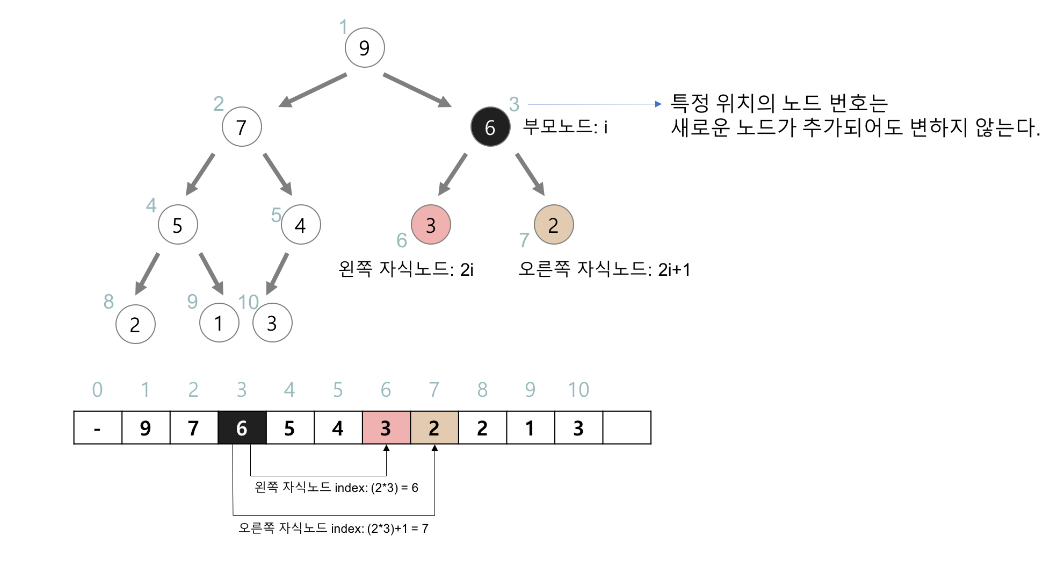
-
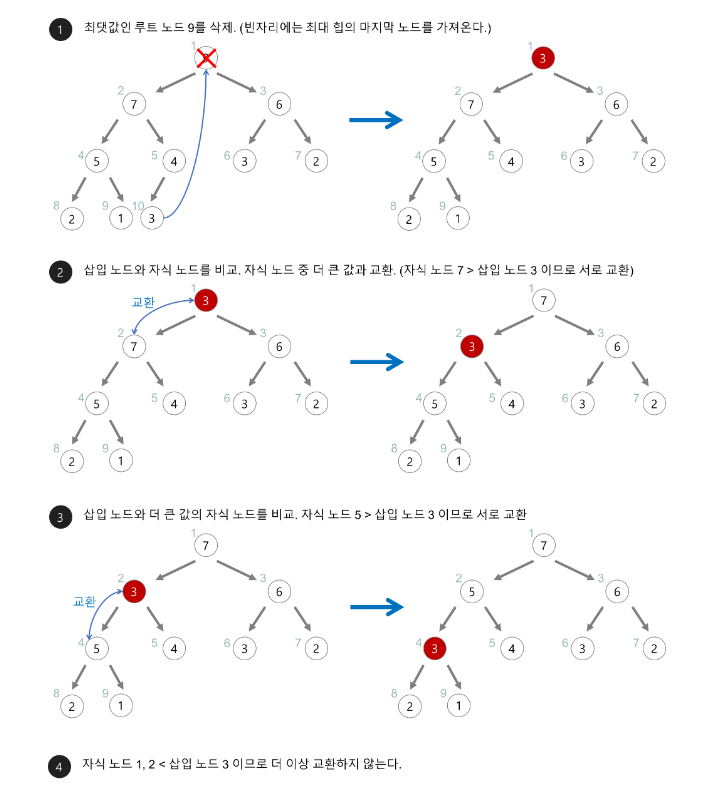
힙의 데이터 삽입
➡ 힙에 새로운 데이터가 들어오면, 새로운 노드를 힙의 가장 마지막 노드 다음에
삽입한다.
➡ 새로운 노드를 부모 노드들과 힙의 성질(최대 힙, 최소 힙)을 만족토록 교환한다.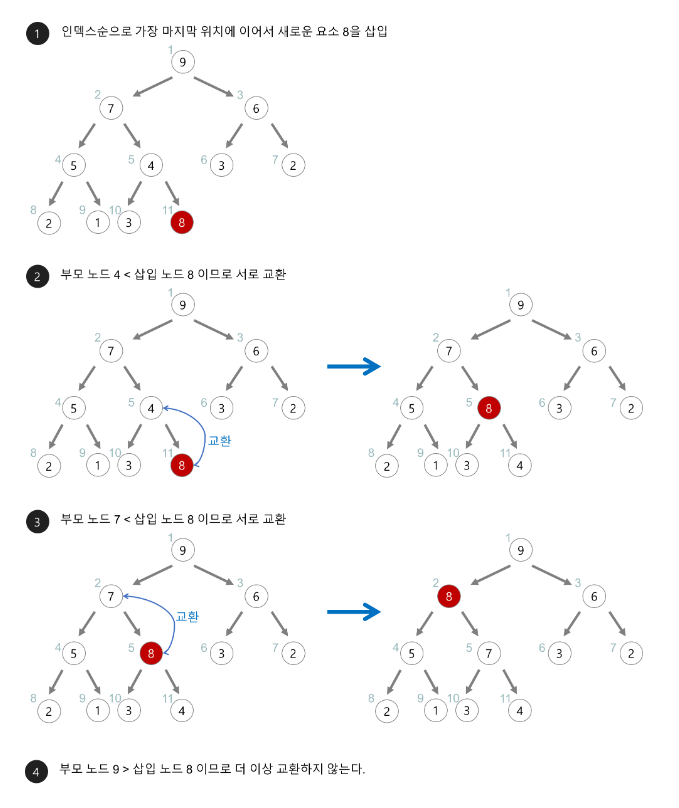
-
힙 정렬 방법
➡ 힙 정렬은 최대 힙 트리(내림차순 정렬) 또는 최소 힙 트리(오름차순 정렬)를 구성하여
정렬하는 방법이다.➡ 최대 힙 정렬 방법 ( 최소 힙도 원리는 같다 )
1) 정렬해야 할 n개의 요소들로 최대 힙을 만든다.
2) 1번째 요소를 힙에서 꺼내서 배열의 뒤부터 저장한다.
3) 제일 마지막 요소를 1번째 요소로 둔 다음 최대 힙을 만족토록 다시 구성한다.
4) 모든 데이터가 꺼내질때까지 2 ~ 3번을 반복한다.
5) 삭제되는 요소들(최대값)은 값이 감소되는 순서로 정렬되게 된다.
💻 코드로 구현 ( 최대 힙 )
// 힙 클래스 생성
public class Heap {
Integer[] arr; // 최초 데이터를 저장할 배열 생성;
Integer[] resultArr; // 최대힙 정렬을 통해 정렬한 결과를 저장할 배열 생성;
public Heap(Integer length) {
// 생성한 두개의 배열 초기화
// 최초 데이터를 저장할 배열의 크기가 length 라면, 최종 정렬한 결과를 저장할 배열의 크기는 length-1
// Why? 최초 데이터를 저장할 배열의 0번 인덱스는 활용하지 않기 위해 데이터를 1개 더 추가해줬기 때문
this.arr = new Integer[length];
this.resultArr = new Integer[length-1];
}
// 최대힙 트리 데이터 삽입 메서드
Integer num; // 데이터를 삽입할 때 인덱스 번호를 저장할 변수 생성
public void add(Integer data) {
// 만약 0번 인덱스에 데이터가 null 이 아니라면(0번 인덱스에 null 을 넣어줄 예정)
if (this.arr[0] != null) {
// 0번 인덱스에 데이터를 삽입한다. 이값은 힙의 구성을 편하게 하기 위한 값으로 건들지 않는다.
this.arr[0] = data;
}
// 그렇지 않으면
else {
// 데이터를 1번 인덱스부터 배열의 크기만큼 반복
for(int i=1; i<this.arr.length; i++) {
// 만약 해당 인덱스에 데이터가 없다면
if (this.arr[i] == null) {
// 해당 인덱스에 데이터를 추가
this.arr[i] = data;
// 이때 num 변수에 인덱스 번호를 저장
this.num = i;
// 새로 추가한 인덱스를 2로 나눈 몫이 0보다 크면 반복한다.
while (this.num/2 > 0) {
int temp = 0; // 데이터를 교환해주기 위해 임시로 데이터를 저장해둘 temp 변수 생성
// 만약 새로 추가한 데이터가 부모 데이터 보다 크다면 부모 데이터와 서로 바꾼다.
if (this.arr[num / 2] < this.arr[num]) {
temp = this.arr[num / 2];
this.arr[num / 2] = this.arr[num];
this.arr[num] = temp;
}
this.num = num / 2;
}
// 데이터 추가가 끝났으면 반복문을 탈출한다.
break;
}
}
}
}
// 데이터 정렬 메서드
public void sort() {
// 구성이 끝난 상태에서 배열의 1번 인덱스를 출력하여 결과 출력 배열(resultArr) 에 데이터를 삽입하고
// 1번 인덱스를 배열의 마지막 인덱스로 바꾸고, 마지막 인덱스는 null 로 값 변경
// 배열의 제일 첫번째 데이터를 결과 배열에 저장한다.
Integer last = this.arr.length-1; // 배열의 마지막 인덱스를 저장할 last 변수 생성
Integer temp = 0; // 부모와 값을 비교할 때 값을 바꿔주기 위해 임시로 저장해 둘 temp 변수 생성
Integer cnt = 1; // 회전 수를 출력하기 위한 cnt 변수 생성
// i가 정렬 배열의 마지막 인덱스부터 0까지 1씩 감소하며 아래의 반복문을 반복한다.
for(int i=this.resultArr.length-1; i>=0; i--) {
// 배열의 첫번째 인덱스를 1로 고정시킨다.
Integer first = 1;
// 만약 정렬 배열에 인덱스가 null 이라면
if(this.resultArr[i] == null) {
// 해당 인덱스에 arr 배열의 1번째 인덱스 데이터를 삽입한다.
this.resultArr[i] = this.arr[first];
// 삽입 후 arr 배열의 1번째 인덱스를 arr 배열의 마지막인덱스로 바꾼다.
this.arr[first] = this.arr[last];
// arr 배열의 마지막 인덱스는 null 로 바꾼다.
this.arr[last] = null;
// arr 배열의 마지막 인덱스 번호를 1뺀다.
last = last - 1;
while (true) {
// 만약 인덱스 값이 arr 배열의 크기보다 커지면 반복문을 탈출한다.
if(first*2+1 >= this.arr.length) {
break;
}
// 만약 왼쪽 자식과 오른쪽 자식 모두 null 이면 비교할 값이 없기 때문에 반복문을 탈출한다.
if(this.arr[first*2+1] == null && this.arr[first*2] == null) {
break;
// 그렇지 않고 만약 왼쪽 자식은 null 이 아니고 오른쪽 자식이 null 이라면(부모와 왼쪽 자식만 비교하면 된다)
} else if(this.arr[first*2+1] == null && this.arr[first*2] != null) {
// 만약 왼쪽 자식이 부모 자식보다 크다면 서로 바꿔준다.
if(this.arr[first] < this.arr[first*2]) {
temp = this.arr[first];
this.arr[first] = this.arr[first*2];
this.arr[first*2] = temp;
// 바꿔준뒤 반복문을 탈출한다.
break;
// 만약 부모가 왼쪽 자식보다 커서 바꿀 필요가 없으면 반복문을 탈출한다.
} else {
break;
}
// 그렇지 않고 만약 왼쪽 자식과 오른쪽 자식 모두 null 이 아니라면
} else if(this.arr[first*2 + 1] != null && this.arr[first*2] != null) {
// 만약 오른쪽 자식이 왼쪽 자식 보다 크다면
if(this.arr[first*2] < this.arr[(first*2) + 1]) {
// 만약 root 가 오른쪽 자식 보다 작다면 서로 바꿔준다.
if(this.arr[first] < this.arr[first*2 + 1]) {
temp = this.arr[first];
this.arr[first] = this.arr[first*2 + 1];
this.arr[first*2 + 1] = temp;
first = (first*2 + 1);
// 그렇지 않으면 반복문을 탈출한다.
} else {
break;
}
}
// 그렇지 않으면
else {
// 1번째 데이터와 왼쪽 자식 데이터와 크기를 비교한다.
// 만약 root 가 왼쪽 자식 보다 작다면 서로 바꿔준다.
if(this.arr[first] < this.arr[first*2]) {
temp = this.arr[first];
this.arr[first] = this.arr[first*2];
this.arr[first*2] = temp;
first = first*2;
// 그렇지 않으면 반복문을 탈출한다.
} else {
break;
}
}
}
}
// 회전 할때마다 배열에 남아있는 데이터를 출력한다.
System.out.print(cnt +" 회전 결과 : ");
for(int j=1; j<this.arr.length; j++) {
System.out.print(arr[j] + " ");
}
System.out.println();
}
// 회전수를 1씩 증가한다.
cnt++;
}
// 최종적으로 정렬된 결과를 출력한다.
System.out.print("최종 정렬 결과 : ");
for(int k=0; k<this.resultArr.length; k++) {
System.out.print(this.resultArr[k] + " ");
}
}
// 최대힙 출력 메서드
public void printHeap() {
System.out.print("모든 데이터 삽입이 끝난 결과 : ");
for(int i=1; i<this.arr.length; i++) {
System.out.print(this.arr[i] + " ");
}
}
}
// ✅ 메인 클래스 생성
public class HeapMain {
public static void main(String[] args) {
Integer randNum;
Boolean flag = true;
Heap heap = new Heap(11);
Integer[] numArray = new Integer[heap.arr.length-1];
heap.add(null); // 0번 인덱스는 null 값으로 고정
// 힙은 중복값을 허용하나, 보기 좋게 결과를 출력하고자 중복값을 없앴다
while(flag) {
flag = false;
for(int i=0; i<numArray.length; i++) {
randNum = (int)(Math.random()*100)+1;
numArray[i] = randNum;
}
for(int i=0; i<numArray.length; i++) {
for(int j=0; j<i; j++) {
if(numArray[i] == numArray[j]) {
flag = true;
}
}
}
}
System.out.print("데이터를 삽입한 순서 : ");
for(int i=1; i<heap.arr.length; i++) {
System.out.print(numArray[i-1] + " ");
heap.add(numArray[i-1]); // 중복되지 않은 숫자를 heap 배열에 넣어준다.
}
System.out.println();
heap.printHeap();
System.out.println();
heap.sort();
}
}
- 출력결과
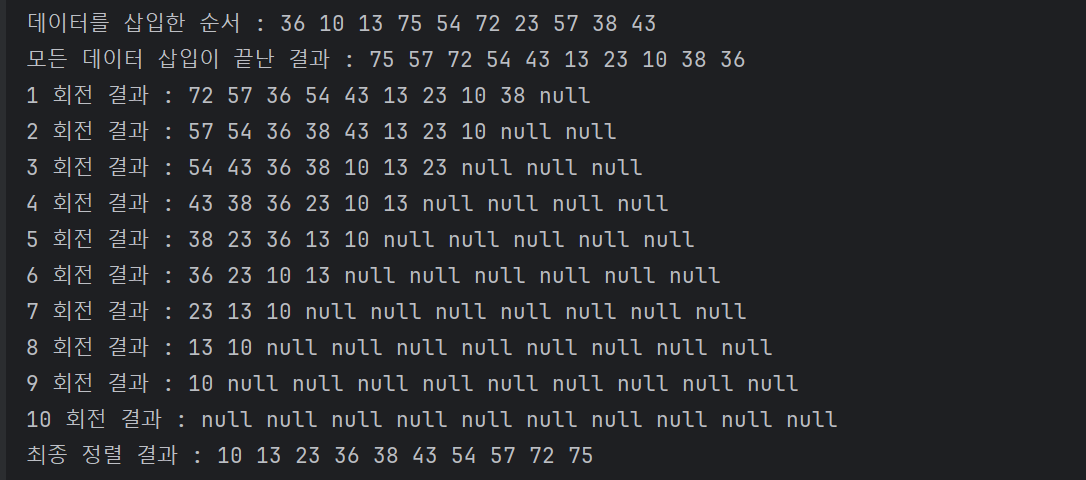➡ 위와 같이 데이터를 삽입했을때 최대 힙으로 구성되고, 거기서 가장 큰 값들이 하나씩
빠져나가면서 정렬되는 것을 볼 수 있다.
오늘의 느낀점 👀
-
오늘은 알고리즘 수업으로 정렬에 대해 배웠다. 글에서 소개한 힙 정렬은 우리조가 담당한 정렬이 힙정렬이라 정리하였지만, 다른 조에서 발표한 것들에 선택 정렬, 거품 정렬, 퀵 정렬, 쉘 정렬, 삽입 정렬, 합병 정렬까지 총 7개를 모두 배우는 시간이었다.
-
그 중에서 가장 어려웠던것은 퀵 정렬이었다고 생각한다. 퀵 정렬은 코드 이해하는데도 시간이 오래걸렸다.
-
우리 조가 맡은 힙 정렬은 기존에 트리에 대한 구조를 이해하고 있었기에 데이터 삽입 기능을 구현해내는건 어렵지 않았다. 하지만 생각보다 정렬 기능을 구현하는데 시간이 오래걸렸는데, 대부분이 배열 인덱스 초과 오류이거나, null 오류 였다. 이것들을 디버깅 해보면서 하나하나 찾아나가서 막판에 딱 원하는 결과가 출력될때 그 짜릿함을 아직도 잊을 수 없다.
-
이런게 코딩의 묘미가 아닌가 싶다. 앞으로도 꾸준히 생각한 대로 코드로 그대로 옮겨보는 연습을 해야겠다.
( 자료참고 : https://gmlwjd9405.github.io/2018/05/10/data-structure-heap.html )
